
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題4「$\chi^2$適合度検定統計量の分布」にPythonを適用して問題を解いていきたいと思います。
今回の記事のコードを使用すれば、自身で仮定した分布に対する$\chi^2$適合度検定を実施することができるようになるので、ぜひみなさんの検定にも活用してみてください!
問題文
<適合度検定: 試合数の分布>
(i) プロ野球日本シリーズでは最初に4勝したチームが優勝する。
両チームが互角で、試合結果が毎回独立なら、引き分けを除くシリーズの試合数$z$の分布は
$$ p(z) = {}_{z-1}\mathrm{C}_3 2^{-z + 1}$$
で与えられることを示せ。
(ii) 次表は1950年から1991年まで42年間の日本シリーズの試合数を示す。試合数が(i)の分布に従うという仮説の$\chi^2$適合度検定を有意水準5%で行え。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 演習問題 P175
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
(i)の証明
実装コードの紹介に入る前に、(i)の証明を簡単に済ませてしましょう。
証明
試合数$z$の分布を考える際には
「どのような条件になれば試合数$z$で全ての試合が終了するのか」
を考える必要があります。
この場合は当然「$z$試合目があるチームにとっての4勝目となる時」が条件になります。
さて、さらに遡って考えると、
「$z$試合目であるチームが4勝目となる」
ための前提条件としては 、
「$z-1$試合中に3勝する必要がある」
ということがわかるかと思います。
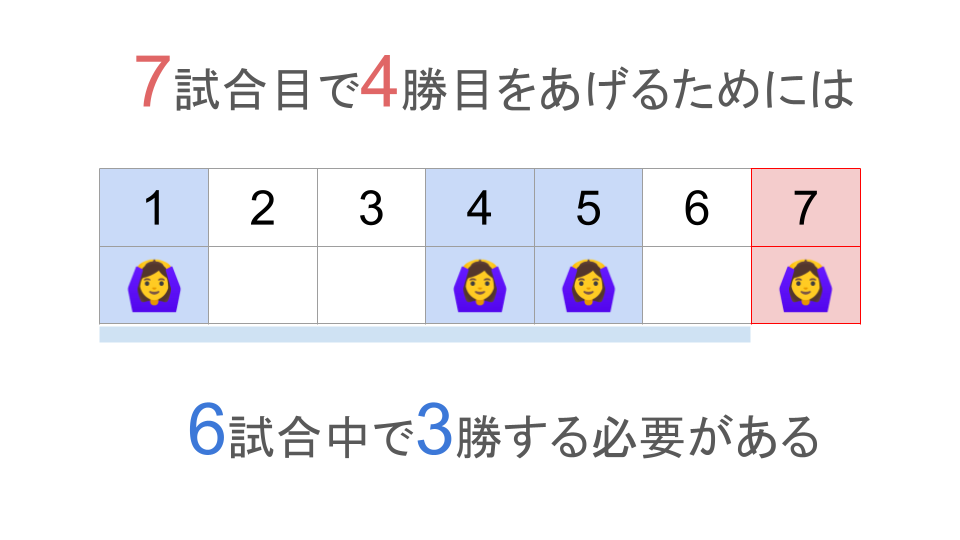
また、$z-1$試合中の3勝はどの試合で上げてもいいので、$z-1$試合の中から3箇所勝つタイミングを選ぶことになります。
そのようなパターンを数式にすると、${}_{z-1}\mathrm{C}_3$と表されます
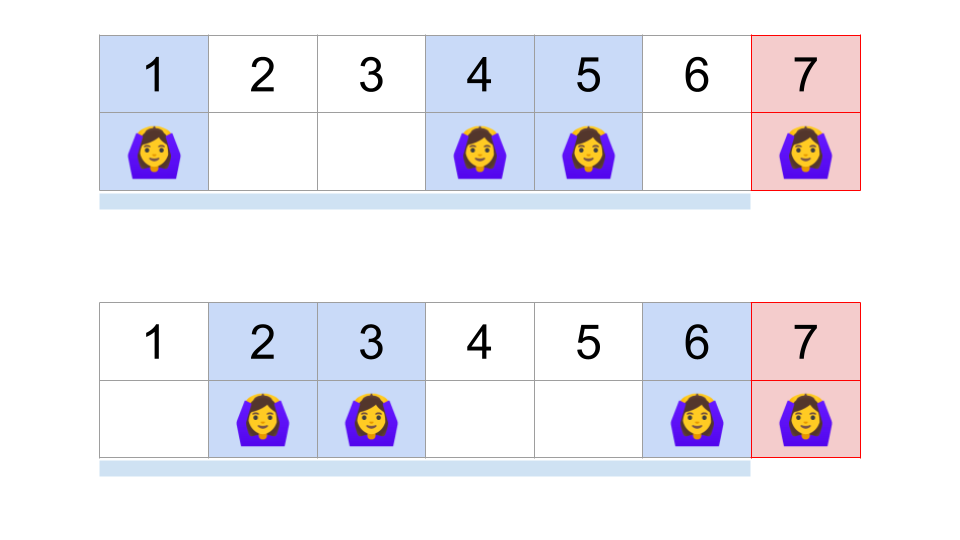
また、$z$試合目に勝つための条件を再度整理すると、以下のようになることがわかります。
- z-1試合中、3試合は勝つ
- z-1試合中、3試合以外、つまりz-4試合は負ける
- z試合目は勝つ
また、「両チームが互角」であることから、勝つ確率は$\frac12$、負ける確率も$\frac12$であることが分かります。
先ほどの3つの条件と「$z-1$試合中、3回勝つタイミングを選ぶ」ことを総合すると、「$z$試合目であるチームが勝つ」ための確率は以下のように求めることができます.
$$ p(z) = {}_{z-1}\mathrm{C}_3 \left(\frac12\right)^3 \times \left(\frac12\right)^{z-4} \times \left(\frac12\right)$$
上記確率はあるチームが$z$試合目に4勝目をあげる確率でしたが、今回の問題においては「両チーム」、つまり2つのチームが存在する過程が置かれています。
つまり、「どちらかのチームが$z$試合目に4勝目をあげる確率」と考えると、両チームが勝つ確率は先ほど求めた確率なので、単純に2倍すればいいことがわかります。
よって、求める確率は
$$ p(z) = {}_{z-1}\mathrm{C}_3 \left(\frac12\right)^3 \times \left(\frac12\right)^{z-4} \times \left(\frac12\right) \times 2 = {}_{z-1}\mathrm{C}_3 2^{-z + 1}$$
となります(証明完了)
実装コード
(ii)を解くための実装コードは以下になります。
import numpy as np
import pandas as pd
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
import math
df = pd.read_csv('Distribution_of_the_number_of_matches.csv')
display(df)
n = df['度数'].sum()
# (i)で証明した確率分布
def calc_prob(z):
c = math.comb(z-1, 3)
prob = c * (2 ** (-z + 1))
return prob
# 期待度数を計算する
df['確率'] = df['試合数'].map(calc_prob)
df['期待度数'] = df['確率'] * n
display(df)
# カイ二乗値を求める
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('仮定した分布は有意水準5%で適合しない')
else:
print('仮定した分布は有意水準5%で適合する')実装コード解説
問題の(ii)は以下の4ステップで解くことができます。
- (i)で証明した確率分布を求める関数を作成する
- 上記関数から確率/期待度数を求める
- 観測度数と期待度数から$\chi^2$値を求める
- 自由度を求め、求めた$\chi^2$値と$\chi^2$分布を比較し、検定する
順を追って解説していきます。
(i)で証明した確率分布を求める関数を作成する
(i)で証明した仮定する分布$ p(z) = {}_{z-1}\mathrm{C}_3 2^{-z + 1}$を関数で実装していきます。
# (i)で証明した確率分布
def calc_prob(z):
c = math.comb(z-1, 3)
prob = c * (2 ** (-z + 1))
return prob${}_{z-1}\mathrm{C}_3$の部分はmathライブラリのcombを使って、math.comb(z-1, 3)と実装できることを覚えておきましょう。
上記関数から確率/期待度数を求める
先ほど作成した確率を求める関数と試合数を使って、分布を仮定した際の確率と求めます。
確率が求め終わったら、求めた確率と全試合数$n$をかけ算して、期待度数を求めます。
# 期待度数を計算する
df['確率'] = df['試合数'].map(calc_prob)
df['期待度数'] = df['確率'] * n
display(df)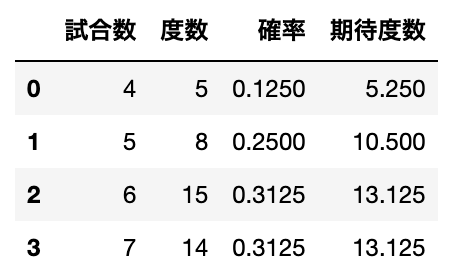
観測度数と期待度数から$\chi^2$値を求める
(観測)度数と先ほど求めた期待度数を使って、$\chi^2$値を求めていきます。
なお、$\chi^2$値を求める式は以下のとおりです。
$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$
# カイ二乗値を求める
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()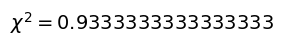
自由度を求め、求めた$\chi^2$値と$\chi^2$分布を比較し、検定する
今回のデータセットと仮定における自由度を求め、自由度と有意水準の値を使って、$\chi^2$分布の値を求めていきます。
なお、今回のデータセットにおいては単純に$(度数の数 – 1)$で自由度を求めることができます。
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('仮定した分布は有意水準5%で適合しない')
else:
print('仮定した分布は有意水準5%で適合する')
自由度3における有意水準5%の時の$\chi^2$値よりも、今回のデータから求めた$\chi^2$値の方が小さいことから、仮定した確率分布$ p(z) = {}_{z-1}\mathrm{C}_3 2^{-z + 1}$はデータに適合していることがわかります。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題4「$\chi^2$適合度検定統計量の分布」にPythonを適用して問題を解いていきました。
今回のように、$\chi^2$適合度検定においては、自身で自由に分布を仮定し、その仮定が正しいのかどうかを検証することができます。
みなさんもぜひ、一般化線形モデルなどのモデルに適合する分布の正しさを検証する際に$\chi^2$適合度検定を活用してみてください!





コメント