
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第10章-演習問題1「2次元のランダムウォーク」について丁寧に解説していきたいと思います。
今回の問題では多項分布についての定義も出てくるのでそちらも合わせて覚えていただけると幸いです
問題文
<2次元のランダムウォーク>
ある粒子は2次元のランダム・ウォークに従い、整数の座標上
$$\{ (i, j) : i, j=, \cdots, -1, 0, 1, \cdots\}$$
を動いているとする。$p, q, r, s$は$0< p, q, r, s < 1, p + q + r + s = 1$を満たす実数とする.
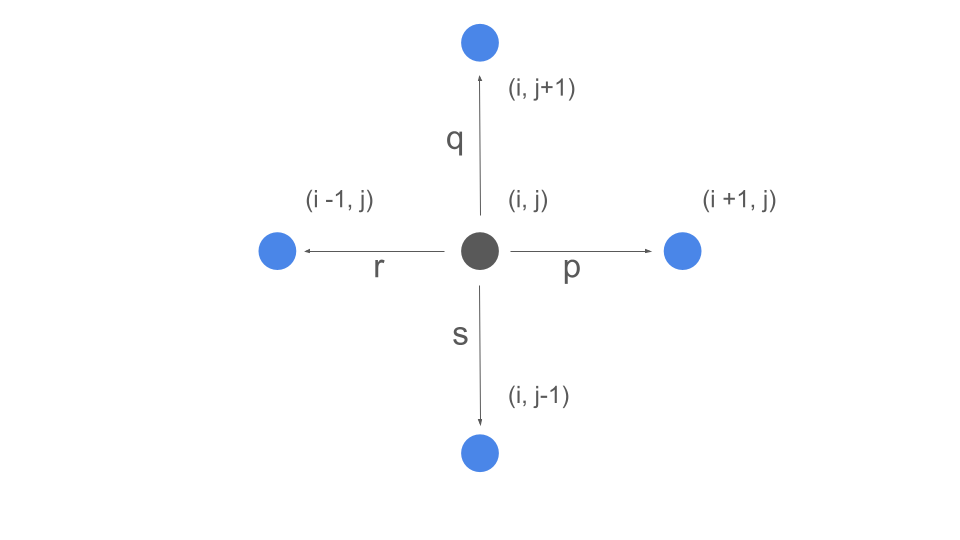
もし時点$n$において粒子が$(i, j)$にいた時、時点$n + 1$には
$$(i + 1, j), (i, j + 1), (i -1, j), (i, j-1)$$
に各々確率$p, q, r, s$で移動する.
また時点毎の移動は互いに独立とする.
時点$0$において原点にいたとして、時点$n$において原点に再び戻る確率を求めよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第10章 P305
多項分布とは?
複数の事象$A_i (i = 1, 2, \cdots, k)$が起きる確率をそれぞれ$p_i (\sum p_i = 1)$とするときに、確率変数$X(X_1, X_2, \cdots, X_k)$が多項分布に従うとき、それぞれの試行が$x_i (x_1 + \cdots + x_k = x)$回起こる確率は次の式から求めることができます.
$$P(X_1 = x_1, \cdots, X_k = x_k) = \frac{x!}{x_1!x_2!\cdotsx_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}$$
ここで、$k=2$の場合について考えてみると、$p_1 + p_2 = 1, x_1 + x_2 = x$であることから上式は以下のように書き換えることができます.
$$P(X_1 = x_1, X_2 = x_2) = \frac{x!}{x_1!x_2!}p_1^{x_1}p_2^{x_2}$$
$$= \frac{x!}{x_1!(x – x_1)!}p_1^{x_1}(1-p_1)^{x-x_1}$$
$$= {}_{x}\mathrm{C}_{x_1} p^{x_1}(1-p_1)^{x -x_1}$$
これは二項分布の確率分布と同一になります。
解説
時点$n$で原点Oに帰ってくるためには、以下の3つの条件を満たす必要があります.
- 上下に等しく$k$回ずつ動くこと
- 左右にも等しく$j$回ずつ動くこと
- 行動回数が偶数回であること(奇数回の場合は上下と左右それぞれの行動回数が等しくなることはない)
よって、上記3つの条件から、$n$について以下のような式を立てることができます.
$$n = 2k + 2j$$
ここで、$m = k + j$とすると、$j = m-k$と表されることがわかり、$k$を変数と見ると、$0 \geqq k \geqq m$であることが分かります。
また、事象を以下のように定めます。
- 右に動く事象$A_1$ → 確率$p$: 回数$k$
- 上に動く事象$A_2$ → 確率$q$: 回数$m-k$
- 左に動く事象$A_3$ → 確率$r$: 回数$k$
- 下に動く事象$A_4$ → 確率$s$: 回数$m-k$
すると、時点$n$において原点Oにいる確率は$0 \geqq k \geqq m$に気をつけると以下のように表すことができます。
$$P(X_1 = k, X_2 = m-k, X_3 = k, X_4 = m-k) = \sum_{k = 0}^{m}\frac{2m!}{k!(m-k)!k!(m-k)!}p^k q^{m-k} r^k s^{m-k}$$
$$= \sum_{k = 0}^{m}\frac{2m!}{(k!)^2((m-k)!)^2}(pr)^2 (qs)^{m-k}$$
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第10章-演習問題1「2次元のランダムウォーク」について丁寧に解説しました!
目標を達成するための条件を整理していき、そのために必要な数学的事項を整理していけば問題なく解けたはずです!
皆さんも1次元、2次元のランダムな挙動に対してはランダム・ウォークの発想を使って、時点$n$における座標を割り出してみてください!



コメント