
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の基本の「き」、分散と標準偏差について解説していきたいと思います!
分散と標準偏差は平均値や中央値、最頻値だけでは表すことができないデータの散らばり具合を表す重要な指標です。
ぜひ本記事で分散と標準偏差の定義やその意味について理解していってください!
平均は同じだけど…?
まずは分散、標準偏差の話に入る前に、データの散らばりについて考えてみましょう。
例えば、次の問題を解いてみてください。
大きさが10の以下の3つのデータA, B, Cについて、それぞれ平均値、中央値、最頻値を求めてください。
A: 0, 3, 3, 5, 5, 5, 5, 7, 7, 10
B: 0, 1, 2, 3, 5, 5, 7, 8, 9, 10
C: 3, 4, 4, 5, 5, 5, 5, 6, 6, 7
平均値とは、データのそれぞれの値の和を、データの個数で割ったものです。

中央値とは、データを値が小さい順(または大きい順)に並べたときに、ちょうど真ん中にくる値のことです。
データが偶数個の場合は真ん中の数字が2個あるので、2つの値を足して2で割った値が中央値になります。
最頻値とは、データの中で最も多くの回数登場している値のことです。
平均値、中央値、最頻値の使う場面や演習も含めた解説については以下の記事が参考になりますので是非ご覧ください。
計算できましたでしょうか?
上記の問題の正解は、「A、B、Cともに平均値、中央値、最頻値はすべて5」となります。
それでは、データ数も平均値、中央値、最頻値が同じであるから、それぞれのデータは全く同じと言えるでしょうか。
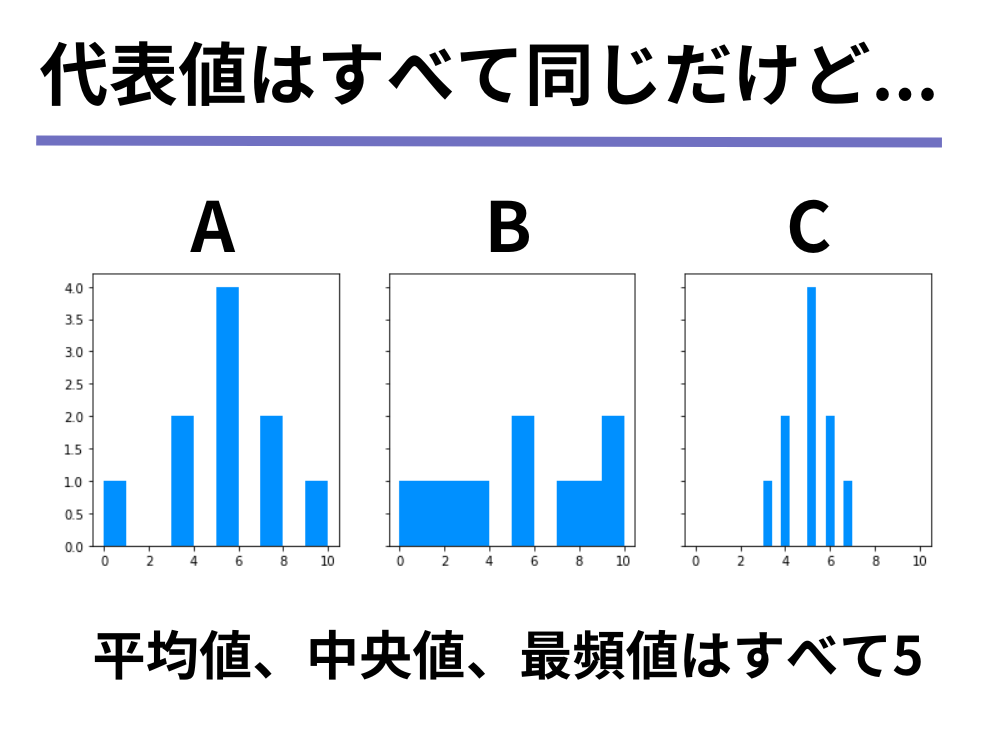
ここで、A、B、Cの分布を可視化したものを見てみましょう。
import matplotlib.pyplot as plt
a = [0,3,3,5,5,5,5,7,7,10]
b = [0,1,2,3,5,5,7,8,9,10]
c = [3,4,4,5,5,5,5,6,6,7]
fig, axes = plt.subplots(1,3, sharey = 'all',sharex = 'all', figsize = (12, 4))
ax = axes.ravel()
ax[0].hist(a, color ="#1e90ff")
ax[1].hist(b, color ="#1e90ff")
ax[2].hist(c, color ="#1e90ff")可視化された分布を見てみると、以下のようなことが分かります。
- データAは0~10の範囲に値が散らばっており、中央付近は特にデータの数が多い
- データBは0~10の範囲にまんべんなく散らばっている
- データCは3~7の範囲に値が集中しており、特に中央付近はデータの数が多い
上記の説明にあるように、データの分布を説明するためには平均値・中央値・最頻値といったデータを代表する値だけでは不十分で、「散らばっている」「集中している」のようなデータの散らばり具合についての指標が必要だということが分かります。
さて、ここまでで勘の鋭い方はお気付きでしょう。
本記事のテーマの分散、標準偏差とは、まさにデータのばらつきを表す指標なのです。
分散とは
分散とは、データのばらつき具合を表す指標であり、以下の4つの計算によって求めることができます。
- データの平均を計算する
- 各データから平均を引いた値を求める
- 2で求めたそれぞれの値を2乗する
- 3で求めたそれぞれの値を足して、データ数で割る
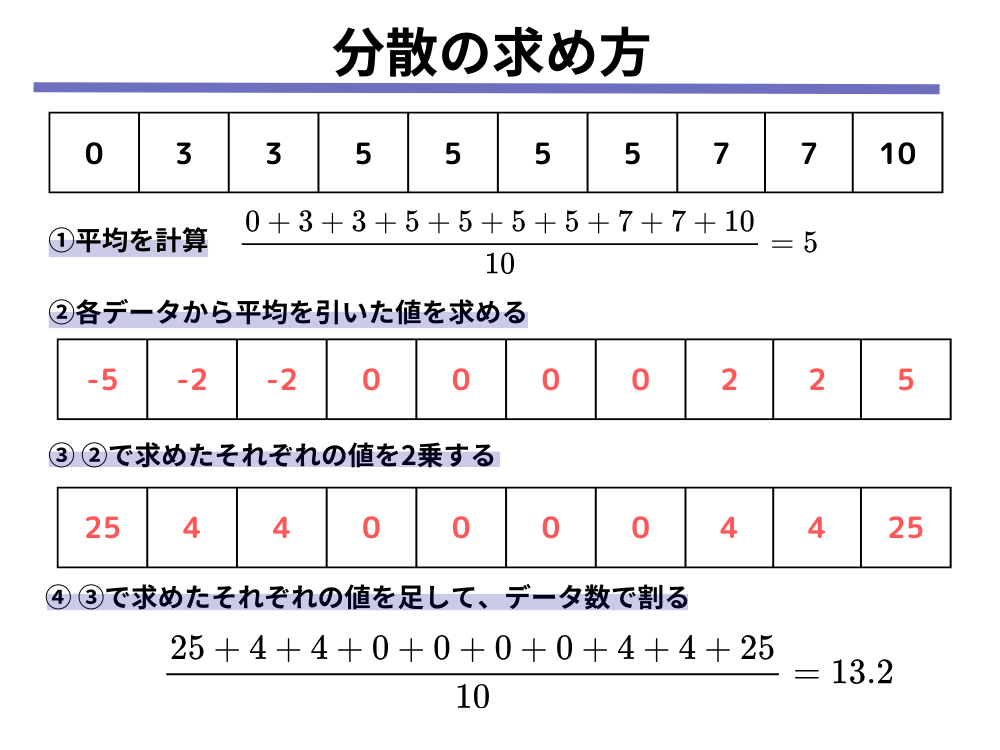
データAについては上記のような計算で、分散は13.2と求めることができます。
データB、データCについても同様の計算手順で求めてみましょう。
B: 0, 1, 2, 3, 5, 5, 7, 8, 9, 10
C: 3, 4, 4, 5, 5, 5, 5, 6, 6, 7
データBについては以下のように計算されます。
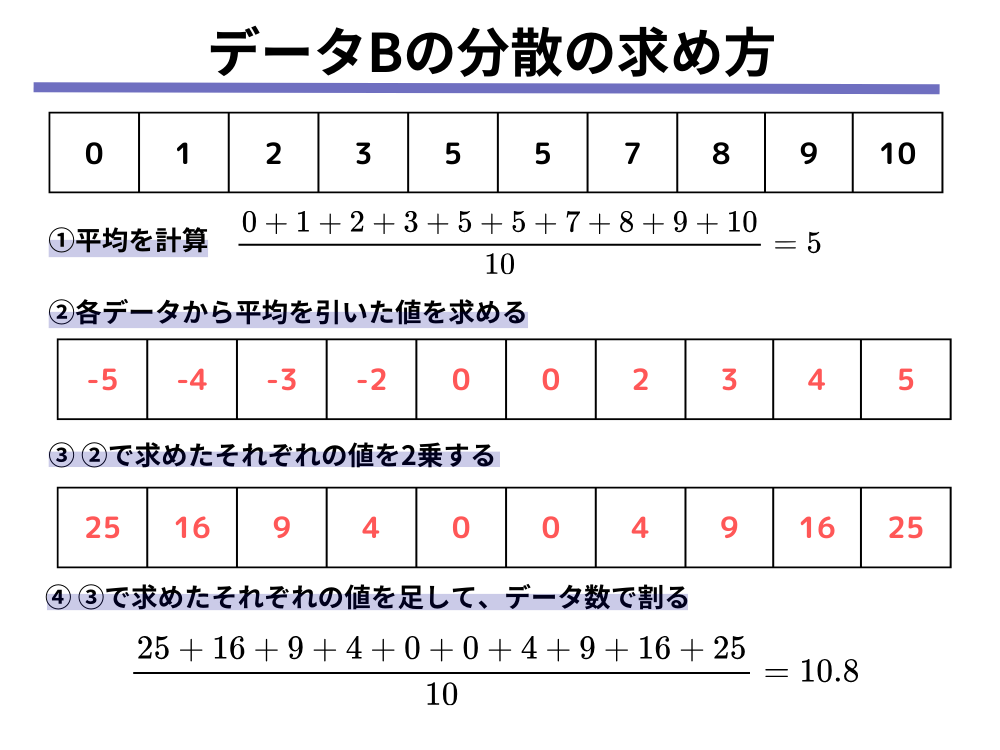
データCについては以下のように計算されます。
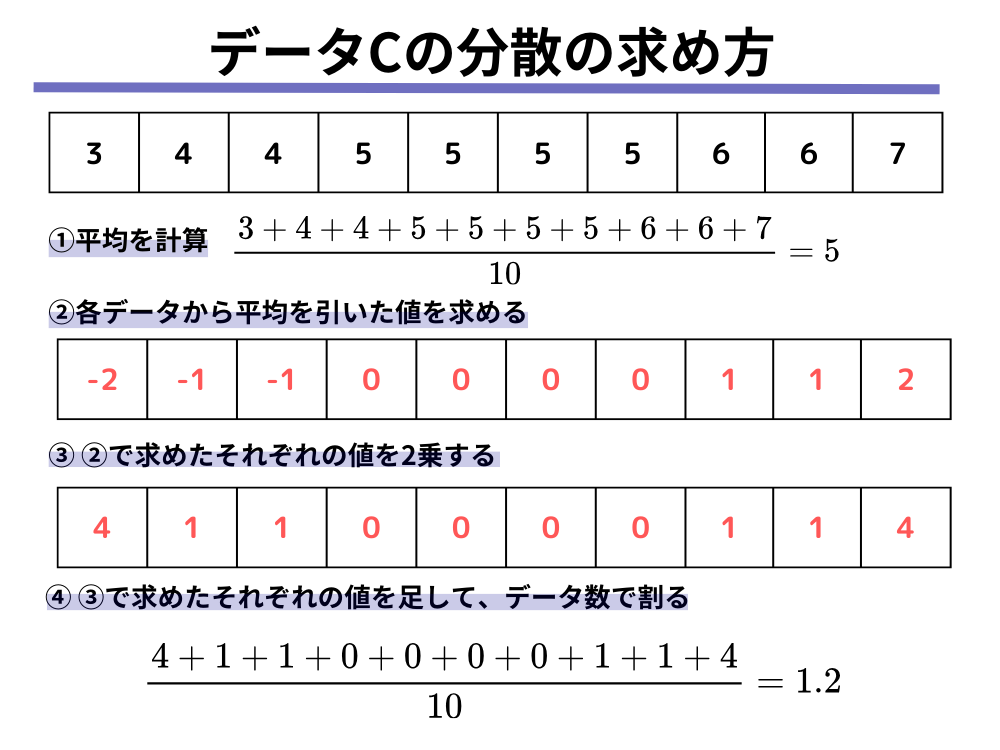
それぞれのデータの分散の値を並べてみると、先ほど分布から読み取ることのできた散らばっている/集中しているという結果と、分散の値が大きい/小さいという結果が一致していることが分かります。
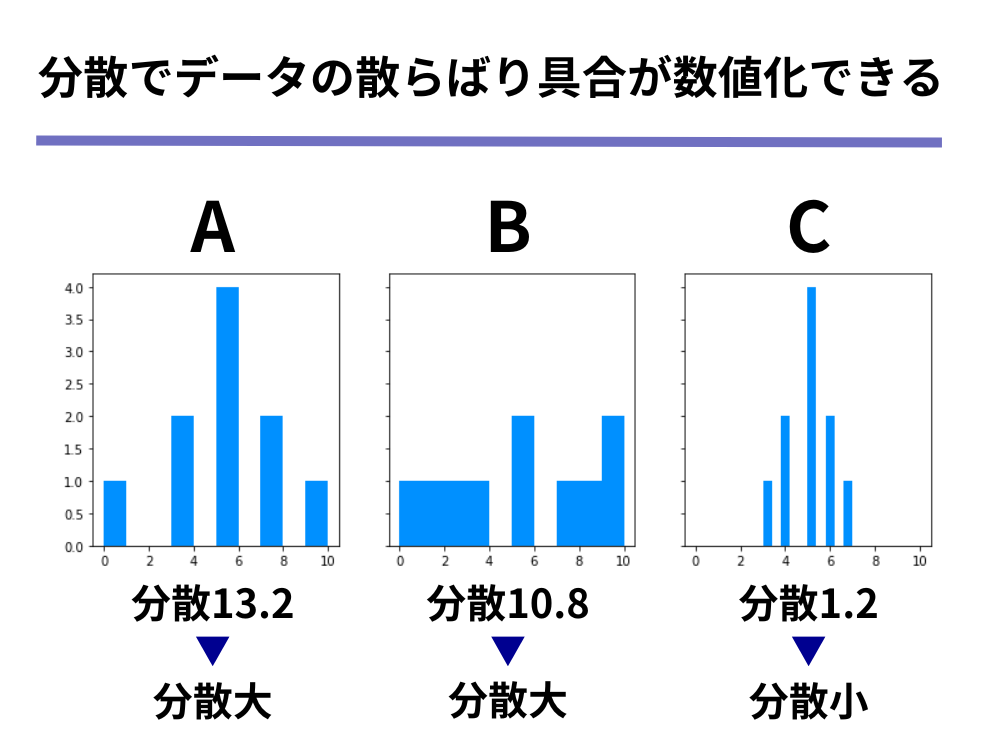
このようにして分散によって、データの散らばり具合という尺度を表現することができるのです。
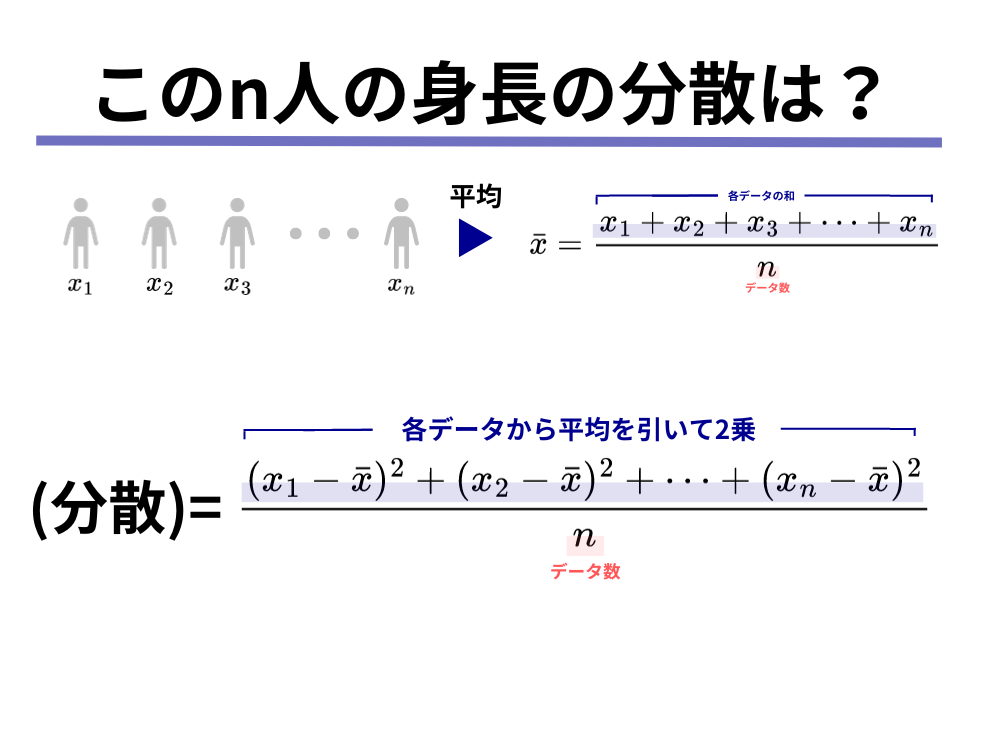
分散の計算手順①〜④をまとめた定義は以下のようになります。
なぜ2乗するのか
先ほど分散の値を求める手順を紹介いたしましたが、このような疑問をお持ちにならなかったでしょうか。

ばらつきを求めるために、平均との差を取る、っていうところまではわかったけど、その後なんで2乗したの?
このような疑問には2つの解を提示させていただきたいと思います。
疑問に対する答え① 2乗しないと…?
それでは、逆に分散の計算において、2乗する過程を飛ばして、以下のような手順で計算するとどうなるでしょうか。
- データの平均を計算する
- 各データから平均を引いた値を求める
2で求めたそれぞれの値を2乗する- 3で求めたそれぞれの値を足して、データ数で割る
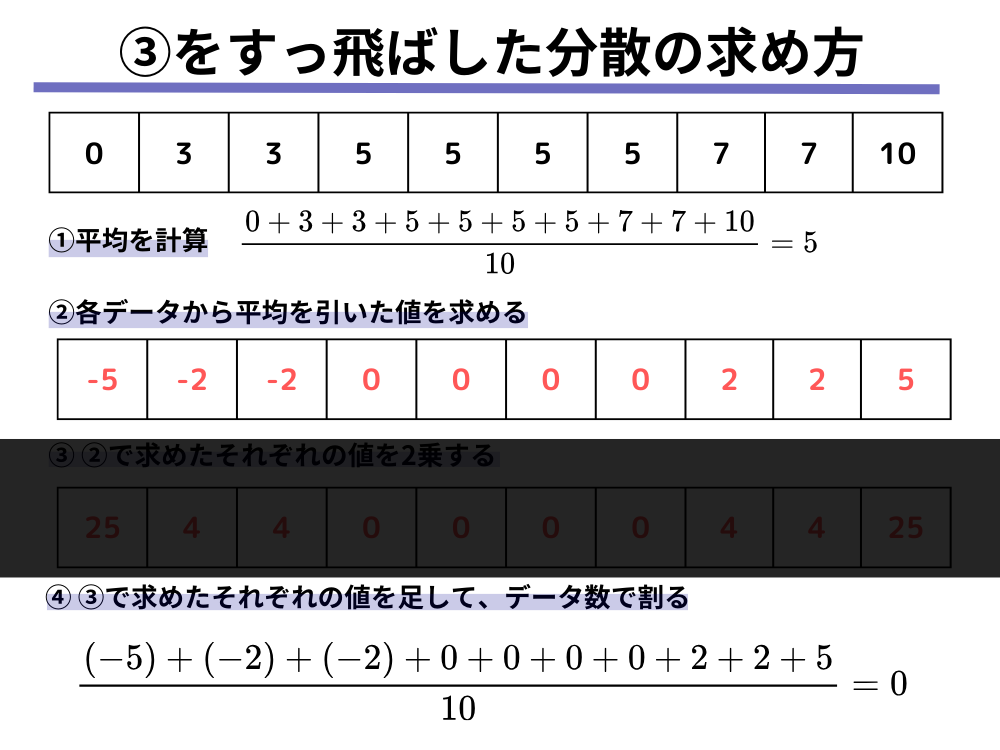
そうなのです、実は2乗をせずに足すと必ず0になってしまうのです。
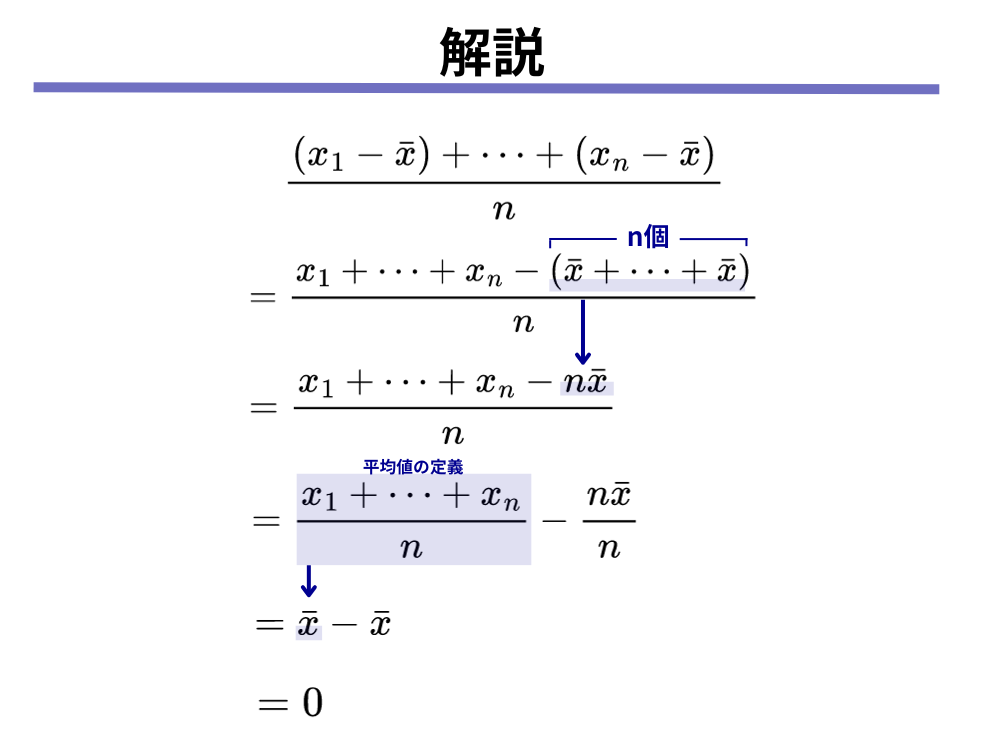
先ほどはデータAを使って、2乗をしない時の和が0になってしまうことを確かめましたが、以下のように一般化した場合でも、2乗をしないと和が0になってしまうことを確かめましょう。
[mathjax]\(n\)個のデータ[mathjax]\(x_1, x_2, \cdots, x_n\)があるときに
[mathjax]$$\frac{(x_1 – \bar{x}) + \cdots + (x_n – \bar{x})}{n}= 0$$
となることを証明してください。
[mathjax]\(\bar{x}=\frac{x_1 + \cdots + x_n}{n}\)であることを利用しましょう。
疑問に対する答え② 分散の「真ん中」がどこになるか
「2乗しないで足し算をすると0になるから2乗をする」というのも説明としてはありなのですが、実は2乗しなくとも0にならないように足し算をすることは可能です。
例えば、各データから平均値を引いた値に、「絶対値」をつけて足し算をすれば足し算の結果は0にはならりません。
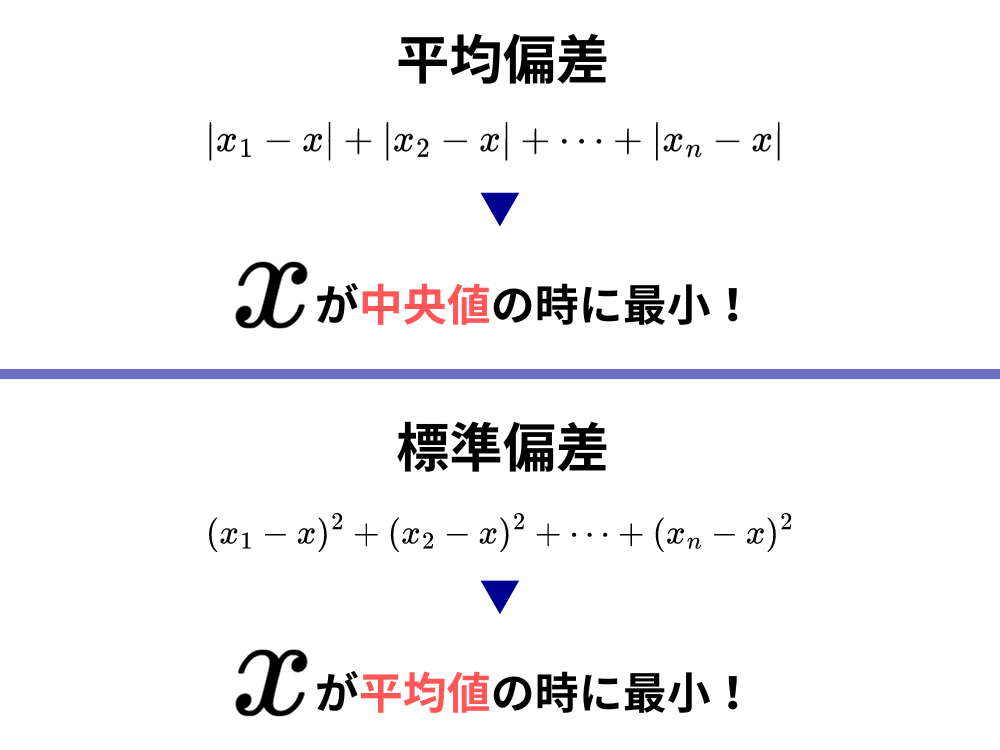
このようにして求めた値を平均偏差と呼びます。
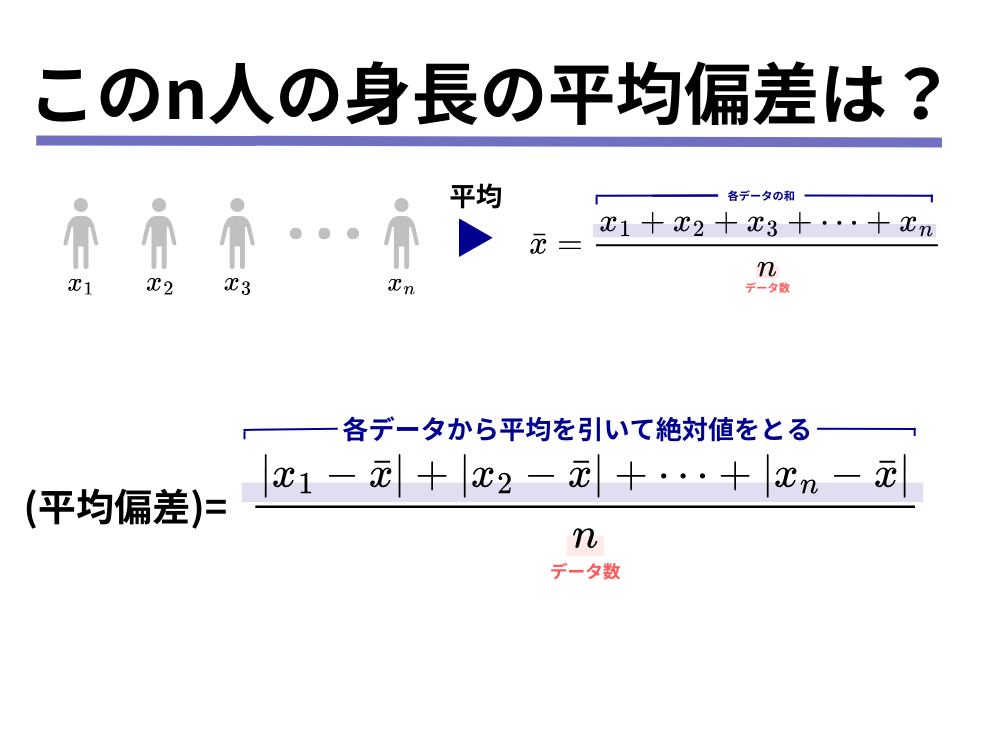
各データの値[mathjax]\(x_i\)とデータの平均[mathjax]\(\bar{x]\)との差のことを偏差と言います。
平均偏差は各データと平均との差を絶対値を使って求めていますし、学校の成績や大学の指標として使われる偏差値も平均値が50になるように調整をした時に、その値より大きいのか小さいのかによって学力的な優劣を図る指標です。
では、なぜ平均偏差を使わずに分散という指標をバラつきの指標として使うことが多いのでしょうか。
答えとしては、「平均偏差と分散で比べると、分散(正確には標準偏差)の方が偏差、つまり平均との差を表すのにふさわしいから」です。

平均との差を表すのにふさわしい???そもそも、今出てきた標準偏差ってなにさ???
というご意見が聞こえてきそうなので、まずは標準偏差について説明し、次に「なぜ平均偏差より標準偏差の方が平均との差を表すのにふさわしいのか」を説明していきます。
標準偏差とは
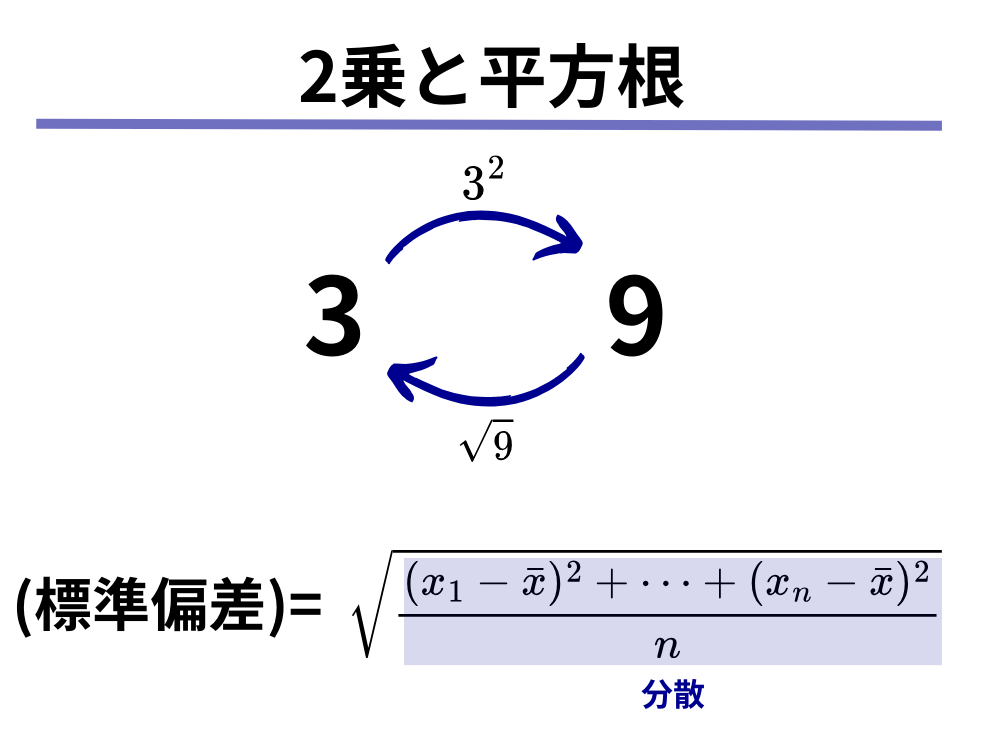
標準偏差とは、分散に平方根(ルート)をとった値です。
つまりは、「勝手に2乗しちゃったから、2乗の逆の操作の平方根(ルート)を取ることによって元に戻す」ようなイメージです。
なぜ平均偏差より分散(標準偏差)の方が平均との差を表すのに相応しいのか?
ここで、新たな問題を考えてみましょう。
それは「分散に定義を一旦頭から忘れた時に、各データから引く値が平均値でなかったとしたら、どんな値が分散を最も小さくするのか」という問いです。

????????
と、頭の中に疑問符が浮かびまくっている方がいるかもしれませんが、ご安心ください。
図示をしながらしっかりと解説させていただきます。
分散の定義では「各データから平均値を引く」ことを大前提としていましたが、「そうじゃなかったら?」を考えてみようということです。(下の図をご覧ください)
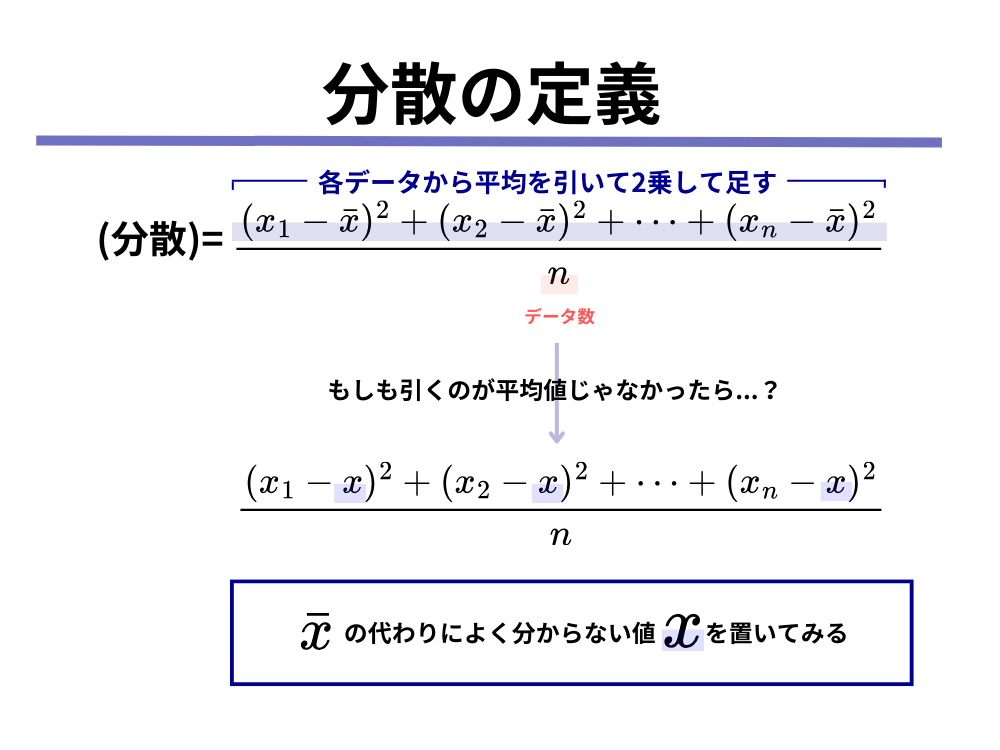
上記のように、「平均値[mathjax]\(\bar{x}\)じゃないよく分からない値[mathjax]\(x\)だったら」を考えてみましょう。
さて、ここで上記の式のうち、[mathjax]\( (x_1 – x)^2 + (x_2 – x)^2 + \cdots + (x_n – x)^2 \)の部分を、展開や平方完成を駆使して計算していくと次のようになります。

以下のように式変形することを平方完成といいます。

ここで、式変形の結果の最後の式
[mathjax]$$ n\left( x – \frac{x_1 + x_2 + \cdots + \x_n}n \right)^2 – \frac{(x_1 + x_2 + \cdots + x_n)^2}n + (x_1^2 + x_2^2 + \cdots + x_n^2)
をグラフで図示すると次のようになります。
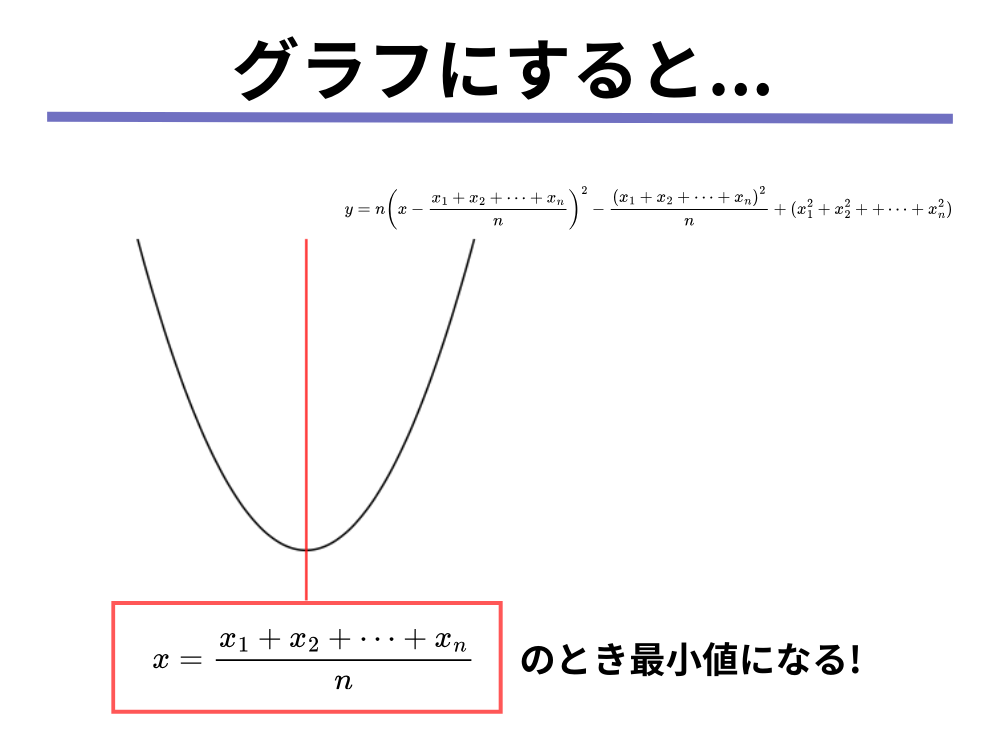
グラフの一番下のところは[mathjax]\( x = \frac{x_1 + x_2 + \cdots + x_n}n\)なので、[mathjax]\( x = \frac{x_1 + x_2 + \cdots + x_n}n\)、つまり[mathjax]\(x\)の値がデータの平均値と等しいときに、[mathjax]\( (x_1 – x)^2 + \cdots + (x_n – x)^2\)の値は最も小さな値になることが分かります。
そして、上の式の[mathjax]\( x\)がデータの平均値であるような式は、まさしく今まで見てきた分散の定義そのものです。
つまり、分散というのはデータから何らかの値を引いて、2乗したものの中で最も小さな値を表すことが分かります。
そして、ここでいう何らかの値とは平均値のことです。
さらに、ここでは詳細な証明はしませんが、平均偏差は引く値が平均値ではなく中央値である時に最小になることがわかっています。
これこそが「平均偏差より標準偏差(または分散)の方が平均との差をよく表現している」と述べた理由です。
分散、標準偏差に関する統計検定3級類似問題
それでは、実際に統計検定3級に出題された問題の類似問題を解きながら、分散と標準偏差の計算方法について復習してみましょう!
次の表は、ある中学校の期末試験における社会の結果です。
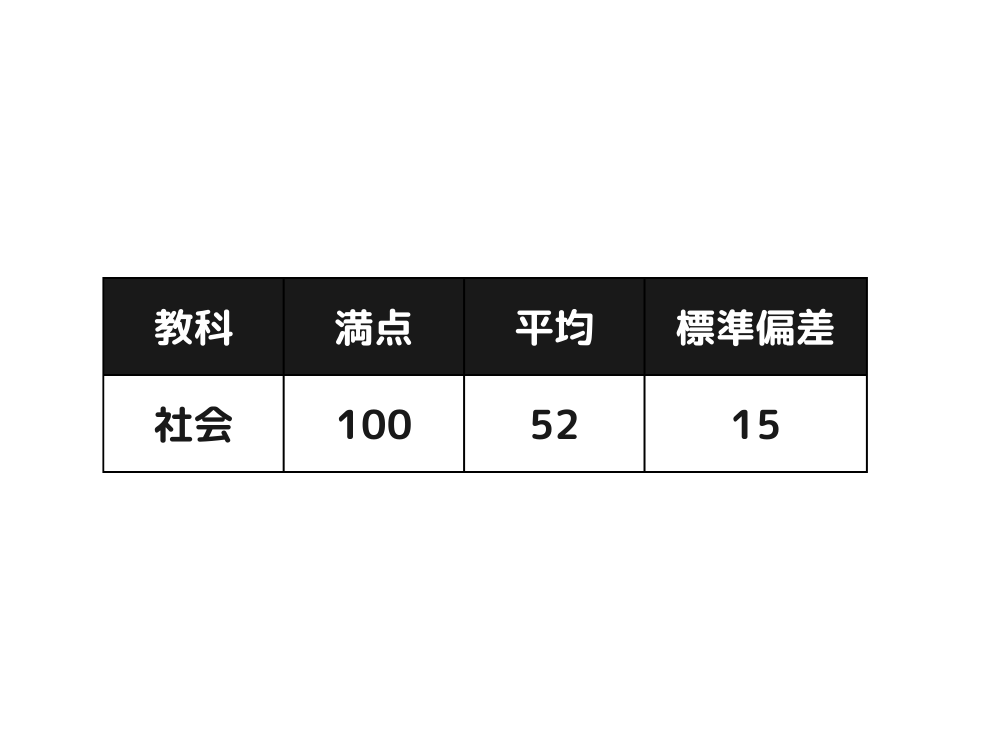
全員の社会の点数に10点を加算することにしました。その際、100点を超えたものはいないものとします。このときの社会の点数の平均点と標準偏差の組み合わせとして、次の1~5の中から適切なものを選んでください。
①平均点: 52 標準偏差: 15
①平均点: 52 標準偏差: 25
①平均点: 62 標準偏差: 15
①平均点: 62 標準偏差: 25
①平均点: 62 標準偏差: 115
平均値と標準偏差がどのようにして計算されていたかを思い出せば解くことができる問題ですので、ぜひ紙に書いて、または頭の中で取り組んでみてください!
前提として、全校生徒は[mathjax]\(n\)人とし、生徒の社会の各点数[mathjax]\(x_1, \cdots, x_n\)とすれば、社会の点数の平均点と標準偏差は以下のような計算式で計算されたことになります。
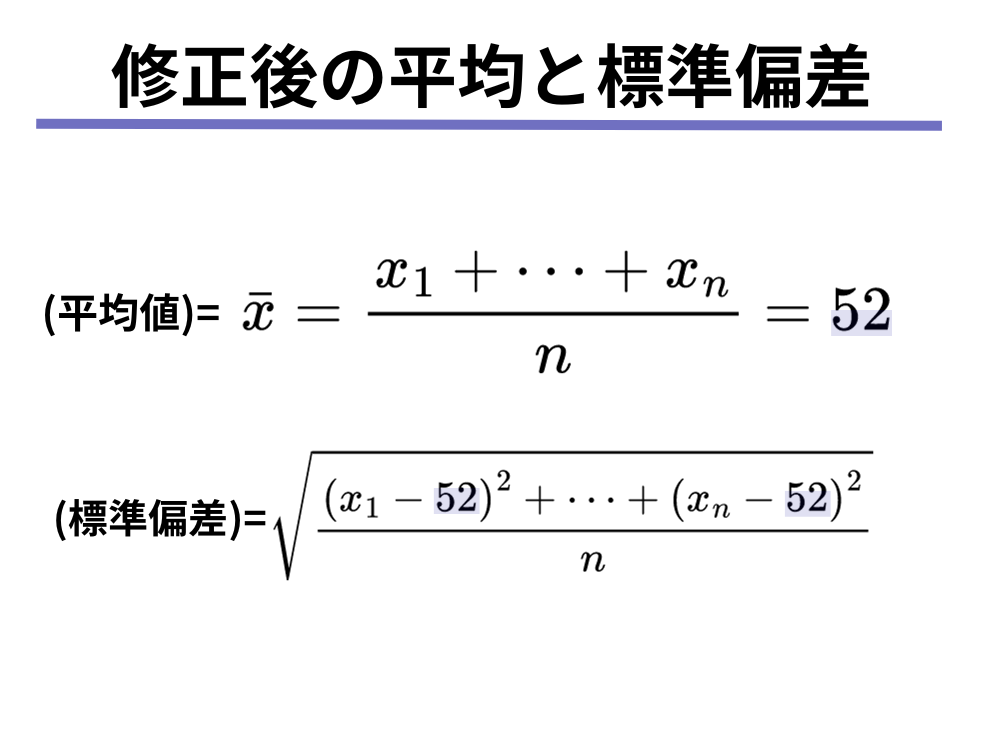
それに対して、全員の社会の点数を10点ずつ加算した後の平均点と標準偏差は、以下のように計算されます。


よって答えは、③平均値: 62 標準偏差: 15となります。
Python/R/SQLでの分散・標準偏差の計算方法
先ほどはテストの社会の点数を使って、分散・標準偏差についての理解を進めていきましたが、今度はPython/R/SQLの問題を解きながら、分散・標準偏差についての理解を進めましょう!
(1)まずはpandasを使ってCSVを読み込んで、mean()やstd()で平均と標準偏差を算出しましょう!
#csvを読み込むためにpandasライブラリをインポート
import pandas
#csv読み込み
df = pd.read_csv('social.csv')
#mean()で平均値を、std()で標準偏差を算出
print('平均点: {}'.format(df['social'].mean()))
print('標準偏差: {}'.format(df['social'].std()))平均点: 52.0
標準偏差: 17.79414451293932(2) social列に10を足し算して、再度平均値と標準偏差を計算してみましょう
#元の点数に10点を加算
df['social'] = df['social'] + 10
#再度平均値と標準偏差を計算
print('平均点: {}'.format(df['social'].mean()))
print('標準偏差: {}'.format(df['social'].std()))平均点: 62.0
標準偏差: 17.79414451293932pandasのstd()メソッドはSTandard Deviation(標準偏差)を計算するメソッドです。
(1)まずはread_csvでcsvを読み込んだ後に、mean()やstd()で平均値、標準偏差を算出しましょう。
#csvを読み込み
df <- read.csv('./social.csv')
#平均値を計算
mean(df$social)
#標準偏差を計算
sd(df$social)>mean(df$social)
[1] 52.0
>sd(df$social)
[1] 17.79414(2)social列に10を足し算して、再度平均値と標準偏差を計算してみましょう
#social列に10を加算
df$social <- df$social + 10
#平均と標準偏差を再度計算
mean(df$social)
sd(df$social)>mean(df$social)
[1] 62.0
>sd(df$social)
[1] 17.79414Pythonでは標準偏差を計算するときはstd()ですが、Rではsd()で標準偏差を計算します。
次のSQL文を実行して、Socialテーブルを定義し、
(1)social列の平均値と標準偏差を計算してください。
(2)social列に10点を加算した時の平均値と標準偏差を計算してください。
CREATE TABLE Social
(
social INTEGER
);
INSERT INTO Social VALUES(43);
INSERT INTO Social VALUES(26);
INSERT INTO Social VALUES(25);
INSERT INTO Social VALUES(41);
INSERT INTO Social VALUES(63);
INSERT INTO Social VALUES(54);
INSERT INTO Social VALUES(40);
INSERT INTO Social VALUES(81);
INSERT INTO Social VALUES(69);
INSERT INTO Social VALUES(16);
INSERT INTO Social VALUES(43);
INSERT INTO Social VALUES(68);
INSERT INTO Social VALUES(73);
INSERT INTO Social VALUES(58);
INSERT INTO Social VALUES(63);
INSERT INTO Social VALUES(69);
INSERT INTO Social VALUES(54);
INSERT INTO Social VALUES(66);
INSERT INTO Social VALUES(53);
INSERT INTO Social VALUES(35);(1)平均の算出にはAVGを、標準偏差の算出にはSTDDEV_SAMPを使用しましょう(PostgreSQL環境を前提としています)
SELECT
AVG(social) as mean,
STDDEV_SAMP(social) as std
FROM
Social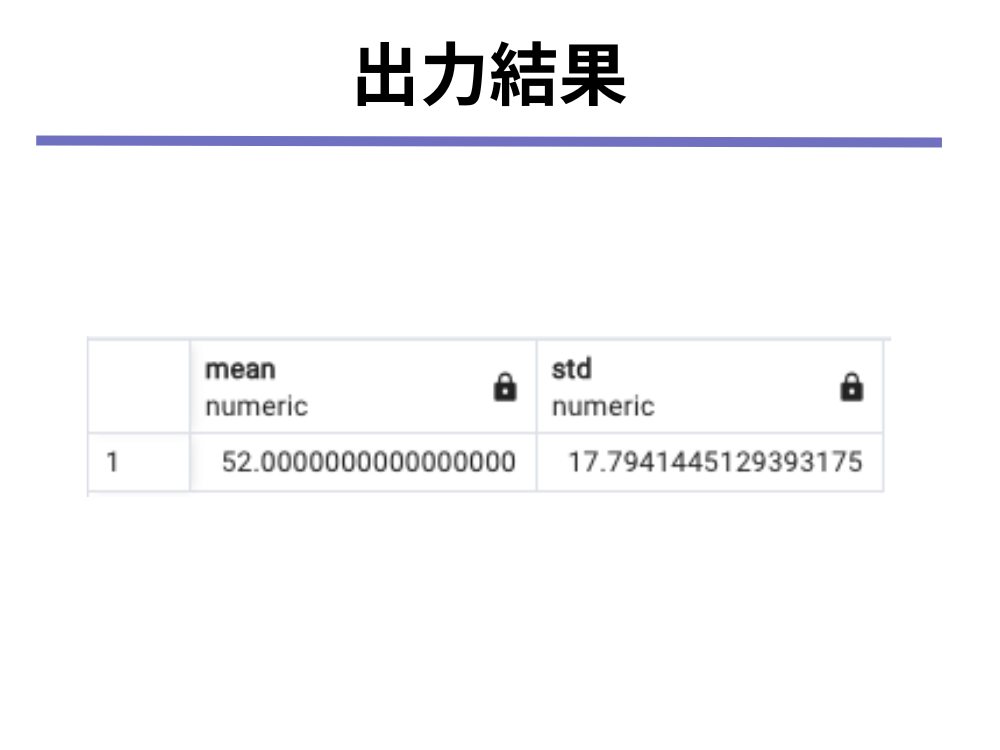
(2)先ほどのクエリのsocial列のところに「+10」を付け加えます。
SELECT
AVG(social + 10) as mean,
STDDEV_SAMP(social + 10) as std
FROM
Social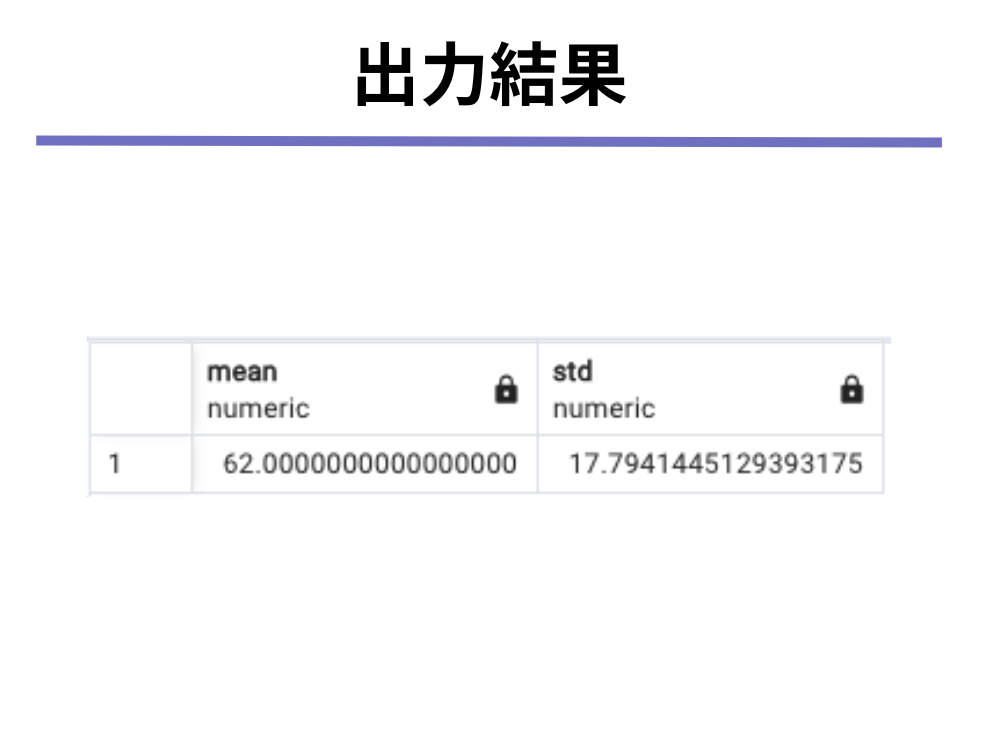
まとめ
この記事では統計学の基礎である分散と標準偏差について、定義から考え方、実践例まで見てきました!
平均と標準偏差は、「平均点が21点のクラスと22点のクラス、その差は本当に意味があるの?」という問いに対して使える重要な考え方ですが、上のような問いに対する答え方については今後記事で解説いたします!
今日も勉強おつかれさまでした!




コメント