「自然科学の統計学」第5章演習1問目の${\chi }^2$適合度検定をPythonで解いてみた

元教師

こんにちは！データサイエンティストの青木和也（https://twitter.com/kaizen_oni）です！

今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題1「${\chi }^2$適合度検定統計量の分布」にPythonを適用して問題を解いていきたいと思います。

${\chi }^2$適合度検定に馴染みのない方でも理解いただけるように解説したので、${\chi }^2$適合度検定のPythonでの実装が気になる方や、数学の問題を通してPythonについての理解を深めたい方はぜひ参考にしてください！

問題文

<${\chi }^2$適合度検定統計量の分布: 近似問題>

多項分布の${\chi }^2$適合度検定統計量の分布は、セルの期待度数が小さい時${\chi }^2$分布で必ずしもよく近似できない。

そのような例として、$n=9,p_1=p_2=p_3=\frac{1}{3}$の三項分布

$$p(x_1,x_2,x_3)=\frac{9!}{x_1!x_2!x_3!}\cdot {\left(\frac{1}{3}\right)}^9\cdots (\ast )$$

で、$(x_1,x_2,x_3)=(6,2,1)$が観測された場合を考えよう。この場合、

$${\chi }^2=\frac{(6-3{)}^2}{3}+\frac{(2-3{)}^2}{3}+\frac{(1-3{)}^2}{3}=\frac{14}{3}=4.67$$

であり、${\chi }_{0.10}^2(2)=4.61$だから、${\chi }^2$近似によれば、4.67以上の値が得られる確率は約10%となる。

近似の良不良を見るためにこの確率を正確に求めてみよう。

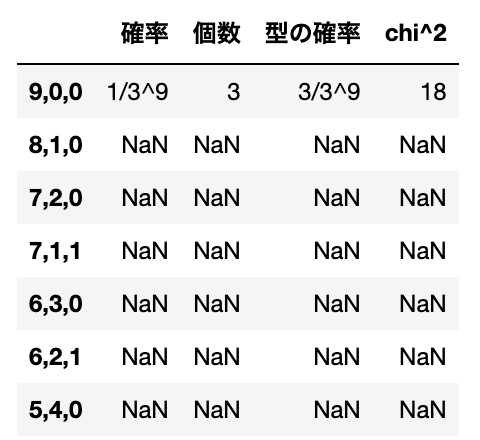
いま、$n=9$を3つに分割する型は全部で12通りあるが、このうち${\chi }^2$が$\frac{14}{3}$以上になるのは下記の7つの型である。

たとえば一番上の9,0,0の確率は$(\ast )$から$\frac{1}{3^9}$であり、そのような型を与える観測値は$(x_1,x_2,x_3)=(9,0,0),(0,9,0),(0,0,9)$の３個だから、型9,0,0の確率は$\frac{3}{3^9}$となる。

他の型についての空欄を埋めて完成し、${\chi }^2\geqq \frac{14}{3}$となる確率が$\frac{3261}{19683}=0.166$となることを確かめよ。

東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 演習問題 P173

実装コード

今回の問題を解く際の実装コードは以下の通りです。

import numpy as np
import math
import pandas as pd

def calc_chi_and_prob(arr):
    sum_chi = 0
    # 確率のうち、分母にある階乗以外の部分を先に計算
    sum_prob = math.factorial(9) / (3**9)
    for val in arr:
        # カイ二乗値を計算
        sum_chi += (val - 3) ** 2/3
        # 分母にある階乗部分を計算
        sum_prob /= math.factorial(val)
    # 数字のペアのうち、一意な数字の個数を求める
    pair = set(arr)
    unique_n = len(pair)
    # 全ての数字が異なる場合は3!がペアのパターン数
    if unique_n == 3:
        pair_num = math.factorial(3)
    # 1つ被りがある場合は3!/2!がペアのパターン数
    else:
        pair_num = math.factorial(3) / math.factorial(2)
    return sum_chi, sum_prob, pair_num

arrs = [
    [9,0,0],
    [8,1,0],
    [7,2,0],
    [7,1,1],
    [6,3,0],
    [6,2,1],
    [5,4,0],
]

arrs = [ calc_chi_and_prob(arr) for arr in arrs]

df = pd.DataFrame(arrs, columns = ['chi_square', 'prob', 'pair_num'])
# ペアごとの期待値を計算
df['E'] = df.prob * df.pair_num
display(df)

# 期待値の合計を計算
print(df.E.sum())

実装コード解説

実装では、以下の4ステップで問題を解いています。

• 当該ペアの確率分布を計算する
• 当該ペアの並び順の個数を計算する
• 当該ペアの${\chi }^2$を計算する
• 各ペアの期待値を計算して、最後に総和を求める

順に解説をしていきます。

当該ペアの確率分布を計算する

当該ペアの確率分布を計算している実装部分は以下のコードです。

def calc_chi_and_prob(arr):
    # ...
    # 確率のうち、分母にある階乗以外の部分を先に計算 ... (1)
    sum_prob = math.factorial(9) / (3**9)
    for val in arr:
        # ...
        # ...
        # 分母にある階乗部分を計算 ... (2)
        sum_prob /= math.factorial(val)

確率分布の計算には以下の式$(\ast )$を使うので、(1)部分で$x_1!x_2!x_3!$以外の部分を計算してから、(2)部分で$x_1!x_2!x_3!$を割り入れて計算をしています。

$$p(x_1,x_2,x_3)=\frac{9!}{x_1!x_2!x_3!}\cdot {\left(\frac{1}{3}\right)}^9\cdots (\ast )$$

なお、math.factorial(n)は$n$の階乗$n!$を意味します。

当該ペアの並び順の個数を計算する

重複を許す3個の数字の並び順を考える場合は、以下の3パターンを考える必要があります。

• 3つとも数字が異なるパターン
• 3つの数字のうち、2つが重複しているパターン（例: 1,1,7）
• 3つの数字の全てが重複しているパターン

本問題の場合はパターン3は登場しないので、パターン1とパターン2について考えましょう。

パターン1の場合はシンプルに3つの数字の並び順を考えれば良いので、以下のように求めることができます。

$$3!=6\mathrm{通}\mathrm{り}$$

一方で、パターン2の場合は、ペアの数字が$7,1_1,1_2$であるとき、$7,1_1,1_2$という並びと$7,1_2,1_1$という並びは同じ並びを意味します。

すると、3つの数字を並べた$3!$通りにおいて、2つの1のせいでパターンが$2!$倍になってしまっているので、これを取り除く必要があります。

$2!$倍を取り除くためには逆演算をしてあげればいいので、3つの数字のうち2つの数字が重複している場合の並び方は以下のようになることがわかります。

$$\frac{3!}{2!}=3\mathrm{通}\mathrm{り}$$

このような場合わけをした上で、並び方のパターン数を計算しているのが以下実装部分になります。

def calc_chi_and_prob(arr):
    # ...
    # 数字のペアのうち、一意な数字の個数を求める
    pair = set(arr)
    unique_n = len(pair)
    # 全ての数字が異なる場合は3!がペアのパターン数
    if unique_n == 3:
        pair_num = math.factorial(3)
    # 1つ被りがある場合は3!/2!がペアのパターン数
    else:
        pair_num = math.factorial(3) / math.factorial(2)

当該ペアの${\chi }^2$を計算する

${\chi }^2$は、以下の式で計算することができます。

$${\chi }^2=\frac{(f_1–n{p}_1{)}^2}{n{p}_1}+\cdots +\frac{(f_k–n{p}_k{)}^2}{n{p}_k}$$

今回のケースでは、$n{p}_k$は常に3なので、以下のように実装することができます。

def calc_chi_and_prob(arr):
    sum_chi = 0
    # ...
    # ...
    for val in arr:
        # カイ二乗値を計算
        sum_chi += (val - 3) ** 2/3

各ペアの期待値を計算して、最後に総和を求める

最後に、計算した確率、並びのパターン数、${\chi }^2$をDataFrameに入れて、(1)それぞれのペアにおける期待値を計算し、(2)期待値の総和を計算します。

df = pd.DataFrame(arrs, columns = ['chi_square', 'prob', 'pair_num'])
# ペアごとの期待値を計算 ... (1)
df['E'] = df.prob * df.pair_num
display(df)

# 期待値の合計を計算 ... (2)
print(df.E.sum())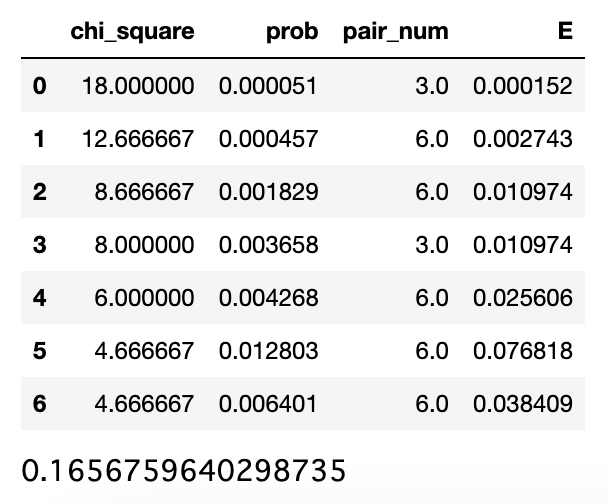

期待値の総和は0.16567…となっており、四捨五入すれば問題文で示唆されている0.166と合致していることがわかります。

まとめ

今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題1「${\chi }^2$適合度検定統計量の分布」にPythonを適用して問題を解く過程を解説いたしました！

確率と並び順の計算自体は高校数学レベル、${\chi }^2$適合度検定については馴染みがないかもしれませんが、公式を適用すれば解くことができるので、統計学をあまり学習されたことがない方にとっても理解しやすいかと思われます。

皆さんも、${\chi }^2$適合度検定を使って、理論値と観測値の間に有意な関係があるか検証してみてください！