
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題2「LD50(半数致死量)など」を数式を使って丁寧に解説していきたいと思います!
今回の問題は(ガウス関数の話を除いて)高校数学の範囲で対応可能な問題となっているので、皆さんもぜひチャレンジしてみてください!
問題文
<LD50など>
プロビット、ロジット・モデルで、$Y_i = 1$となる反応確率
$$ P = F(\beta_0 + \beta_1 X)~~~(F = \Phi, \Lambda)$$
に対し、次の$X$の値をそれぞれ求めよ。
i ) P = 1/2となる$X$の値
ii ) |dP/dX|が最大になる$X$の値とそれに対する|dP/dX|の値
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章 演習問題 P229
プロビットモデル・ロジットモデルとは?
プロビットモデルとは、1/0のような二値$Y_i$を予測するような回帰問題において、説明変数が$X_i$であるとすると、条件付き確率
$$P(Y_i|X_i) = F^*(X_i)$$
の$F^*(X_i)$に標準正規分布を仮定する時の予測モデルのことを言います。
$$標準正規分布の累積分布関数~~~F^*(X_i) = \Phi(\beta_0 + \beta_1 X_i) = \int_{-\infty}^{\beta_0 + \beta_1 X_i} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$$
一方で、$F^*(X_i)$にロジスティック分布を仮定するとき、そのモデルをロジットモデルと呼びます。
$$ロジスティック分布の累積分布関数~~~F^*(X_i) = \Lambda(\beta_0 + \beta_1 X_i) = \frac{e^{\beta_0 + \beta_1 X_i}}{1 + e^{\beta_0 + \beta_1 X_i}}$$
この2つの関数が条件付き確率の分布の仮定に使用されている大きな理由は、累積分布関数が0~1に収まるという性質が、「確率は0%~100%に収まっていて欲しいよね」という点とマッチするからです。
(i)の解答
プロビットモデル$\Phi$の場合
$\Phi(\beta_0 + \beta_1 X) = \int_{-\infty}^{\beta_0 + \beta_1 X} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$について考える前に、まずは$\int_{-\infty}^{\infty} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$について考えてみましょう。
この時、$\int_{-\infty}^{\infty} e^{-x^2/2}dx$はガウス積分そのものであるので、
$$\int_{-\infty}^{\infty} e^{-x^2/2}dx = \sqrt{2\pi}$$
となり、
$$\int_{-\infty}^{\infty} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx = 1$$
となることがわかります。
ガウス積分の公式
$$\int_{-\infty}^{\infty} e^{-ax^2}dx = \sqrt{\frac\pi{a}}$$
また、$e^{-x^2/2}$は偶関数($y$軸対象)であるので、
$$\int_{-\infty}^0 \frac1{\sqrt{2\pi}}e^{-x^2/2}dx = \int_0^\infty \frac1{\sqrt{2\pi}}e^{-x^2/2}dx = \frac12$$
であることがわかる。
つまり、$P = \frac12$が成り立つためには、
$$\int_{-\infty}^0 \frac1{\sqrt{2\pi}}e^{-x^2/2}dx = \int_{-\infty}^{\beta_0 + \beta_1 X} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$$
が成り立つ必要があるため、
$$\beta_0 + \beta_1 X = 0$$
であることがわかる。よって、
$$X = -\frac{\beta_0}{\beta_1}$$
ロジットモデル$\Lambda$の場合
$P = \frac12$より
$$\frac12 = \frac{e^{\beta_0 + \beta_1 X}}{1 + e^{\beta_0 + \beta_1 X}}$$
両辺に$2(1 + e^{\beta_0 + \beta_1 X})$をかけ算して、
$$1 + e^{\beta_0 + \beta_1 X} = 2 e^{\beta_0 + \beta_1 X}$$
$$ e^{\beta_0 + \beta_1 X} = 1$$
$$\beta_0 + \beta_1 X = 0$$
よって、
$$X = -\frac{\beta_0}{\beta_1}$$
(ii)の解答
プロビットモデル$\Phi$の場合
$$\frac{d}{dx}\left(\int_c^x f(t)dt\right) = f(x)$$
であることを利用すると、
$$\frac{dP}{dX} = (\beta_0 + \beta_1 X)’ \frac1{\sqrt{2 \pi}} e^{-(\beta_0 + \beta_1 X)^2/2} =\frac{\beta_1}{\sqrt{2 \pi}} e^{-(\beta_0 + \beta_1 X)^2/2} $$
ここで$dP/dX$をもう一度$X$について微分すると
$$\frac{d^2P}{dX^2} = -\frac{\beta^2_1}{\sqrt{2\pi}}(\beta_0 + \beta_1 X)e^{-(\beta_0 + \beta_1 X)^2/2}$$
$\frac{d^2P}{dX^2}=0$の時、$X = -\frac{\beta_0}{\beta_1}$
よって、増減表を書くと以下のようになる
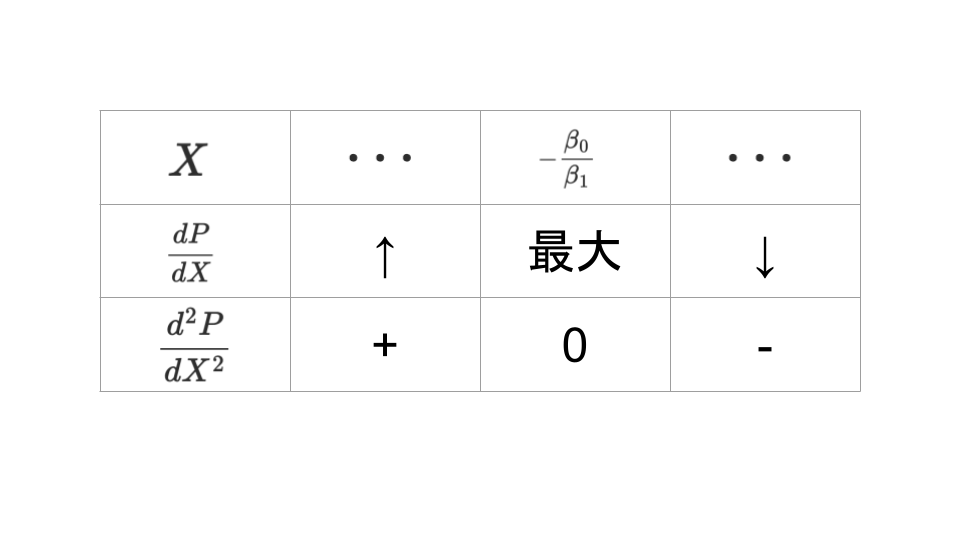
よって、$X = -\frac{\beta_0}{\beta_1}$の時の$|dP/dX|$の値は
$$\left|\frac{dP}{dX}\right| = \frac{\beta_1}{\sqrt{2\pi}} = 0.3989\beta_1$$

ロジットモデル$\Lambda$の場合
$$\frac{dP}{dX} = \frac{\beta_1 e^{\beta_0 + \beta_1 X}(1 + e^{\beta_0 + \beta_1 X}) – \beta_1 e^{\beta_0 + \beta_1 X}\times e^{\beta_0 + \beta_1 X}}{(1 + e^{\beta_0 + \beta_1 X})^2}$$
$$= \frac{\beta_1 e^{\beta_0 + \beta_1 X}}{(1 + e^{\beta_0 + \beta_1 X})^2} = \frac{\beta_1}{1 + e^{\beta_0 + \beta_1 X}}\times P$$
さらに$X$について微分すると
$$\frac{dP^2}{dX^2} = -\frac{\beta^2_1e^{\beta_0 + \beta_1 X}}{(1 + e^{\beta_0 + \beta_1 X})^2}\cdot P +\frac{\beta_1}{(1 + e^{\beta_0 + \beta_1 X})}\cdot \frac{dP}{dX}$$
$$= -\frac{\beta^2_1e^{\beta_0 + \beta_1X} \times e^{\beta_0 + \beta_1X}}{(1 + e^{\beta_0 + \beta_1 X})^3} + \frac{\beta_1}{1 + e^{\beta_0 + \beta_1X}}\cdot \frac{\beta_1e^{\beta_0 + \beta_1X}}{(1 + e^{\beta_0 + \beta_1X})^2}$$
$$ = \beta^2_1 \cdot \frac{e^{\beta_0 + \beta_1X} (1 – e^{\beta_0 + \beta_1X})}{(1 + e^{\beta_0 + \beta_1X})^3}$$
よって、$\frac{d^2P}{dX^2} = 0$の時、$X = -\frac{\beta_0}{\beta_1}$
増減表を書くと、以下のようになる
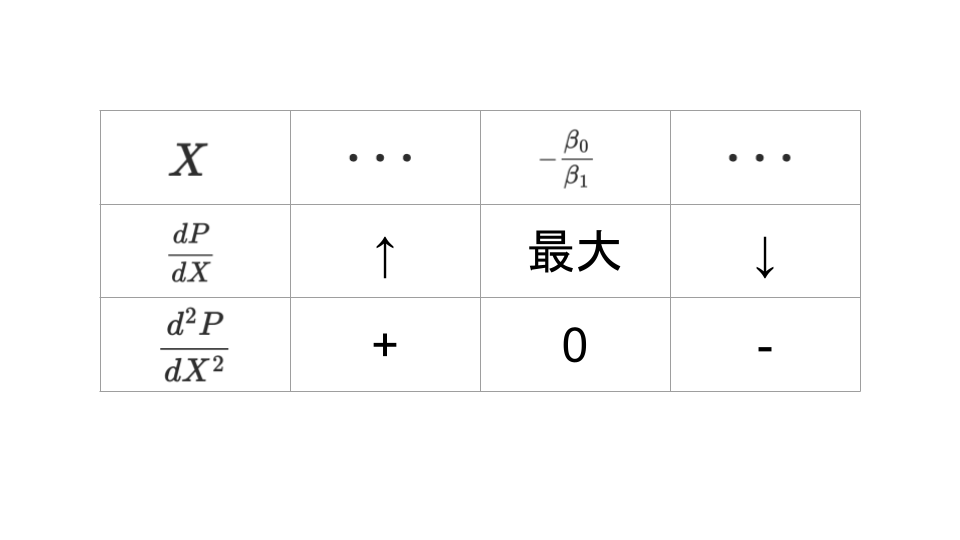
よって、$X = -\frac{\beta_0}{\beta_1}$の時の$|dP/dX|$の値は
$$\left|\frac{dP}{dX}\right| = \frac{\beta_1}{(1+1)^2} = 0.25\beta_1$$
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題2「LD50(半数致死量)など」を数式を使って丁寧に解説してみました!
増減表など高校ぶりに見た方も多かったのではないでしょうか?
標準正規分布とロジスティック分布の形からして自明な証明ではありましたが、頭の体操という点で皆さんの数学・統計力アップに寄与できていれば幸いです!



コメント