
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第1章-演習問題3「負の二項分布」を丁寧に解説していきたいと思います。
今回の問題の解法は正直「そんな解き方ありかよ!」と思えるものなので、頭を柔らかくして考えていただけると幸いです。
問題文
<負の二項分布>
負の二項分布に従う確率変数$X$の期待値を求めよ
(ブログ主追記)なお、求める期待値は$k$回成功するまでに要する回数の期待値とする
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第1章 P22
負の二項分布とは?
成功と失敗のある試行に置いて、成功事象$S$が$M$回発生するまでに要した回数を$X$回とした時、以下の確率関数で表現される分布のことを負の二項分布という。
なお、すべての試行回数は$n$回とする。
$$P(X – n) = {}_{n-1} \mathrm{C}_{M-1} p^M q^{n-M}$$
上の式は「$n-1$回目までのどこかで$M-1$回の成功をしていて、最後の$n$回目で$M$回目の成功をする」ということを表している
幾何分布とは?
ある試行について、最初の成功$S$が出現するまでの試行回数を$x$とするとき、成功する確率を$q = 1-p$とすると
$$f(x) = pq^{x-1}, ~~~x = 1,2,3,\cdots$$
を幾何分布の確率密度関数として定義する。
第1章の演習問題2では幾何分布の期待値$E(X)$が$\frac1p$であることを求めた。
解説
負の二項分布は「$k$回」成功するまでの回数$X$を確率変数とする確率分布であった。
一方で、幾何分布は「最初に」成功するまでの回数$X$を確率変数とする確率分布であった。
よって、負の二項分布において、$k=1$とすると、負の二項分布の確率分布は幾何分布の確率分布に一致するはずである。
逆に言えば、幾何分布において、成功するたびに「ポカンッ!」と記憶を無くして、再度「最初に」成功するまでの試行を繰り返し、「結果として」$k$回成功したところでストップすると考えれば、$k$回成功するまでの回数の分布・負の二項分布は、幾何分布の試行を$k$回繰り返すことと等しい。
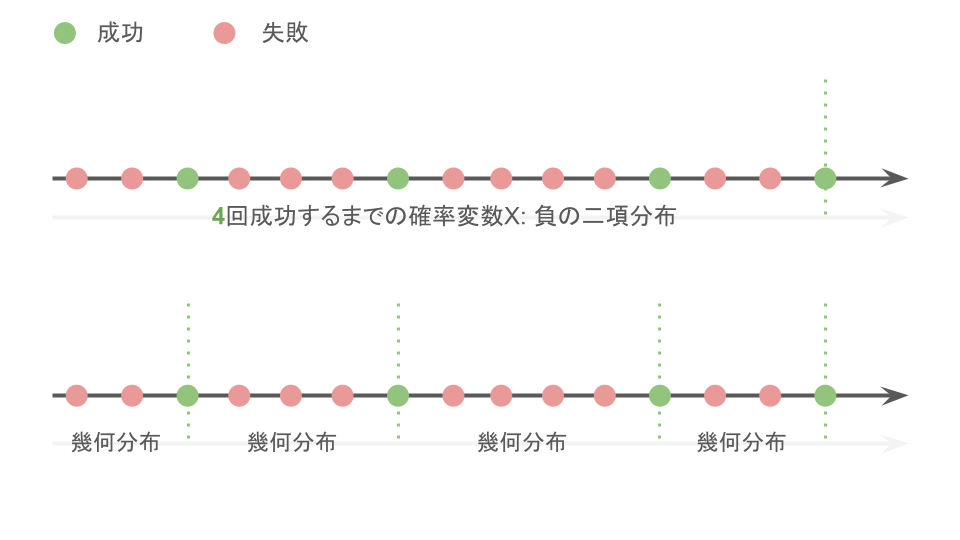
よって、$Y_i(i = 1,2,\cdots, k)$が互いに独立で、パラメータ$p$の同一の幾何分布に従うとすると、
$k$回成功するまでの負の二項分布の確率変数$X$は、以下の式で表される。
$$X = Y_1 + Y_2 + \cdots + Y_k$$
よって、両辺の期待値を取ると、
$$E(X) = E(Y_1) + E(Y_2) + \cdots + E(Y_k) = \frac1p + \frac1p + \cdots + \frac1p = \frac{k}p$$
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第1章-演習問題3「負の二項分布」を丁寧に解説していきました。
幾何分布の延長線上に負の二項分布がある、ということを理解いただければ今回の解法についてはすんなり理解いただけるのではないかと考えております。
皆さんの独学のお役に立てれば幸いです!




コメント