
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第6章-演習問題2「母平均についての2標本問題」にPythonを適用して問題を解いていきたいと思います。
今回の問題では副次的に上側確率や累積分布関数についても学ぶことができるので、検定をPythonで実装したことのない方はぜひ参考にしてみてください!
問題文
<母平均についての2標本問題>
正規分布の母平均$\mu$に関する2標本問題で、(6.16)式を用いて、$m=n=5,~\mu_1-\mu_2=1,~\sigma_0 = 1$の場合の検出力を求めよ
※(6.16)式は以下の通り
片側検定
$$ \beta_{\sigma}(\mu_1, \mu_2) = 1 – \Phi(z_{\alpha} – \tau)$$
両側検定
$$ \beta_{\sigma}(\mu_1, \mu_2) = 1 – \Phi(z_{\alpha/2} – \tau) + \Phi(-z_{\alpha/2} – \tau)$$
※$\tau$の導出は以下の通り
$$\tau = \sqrt{\frac{mn}{(m+n)}}\frac{(\mu_1 – \mu_2)}{\sigma_0}$$
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 演習問題 P199
$m,n$は何を表すのか
今回の問題における$m,n$はそれぞれの正規分布における標本数を表します。
つまり、以下のような式が成り立ちます。
$$\mu_1 = \frac{\sum_{i=1}^m X_i}{m}$$
$$\mu_2 = \displaystyle\frac{\sum_{i=1}^n X_i}{n}$$
$\Phi(z)$は何を表すのか
統計学においては$\Phi(z)$というのは標準正規分布の累積分布関数を表します。
計算式は以下のようになります。
$$ \Phi(z) = 1- Q(z) = 1 – \frac1{\sqrt{2\pi}}\int_z^{\inf} \exp\left(-\frac{u^2}2\right)du$$
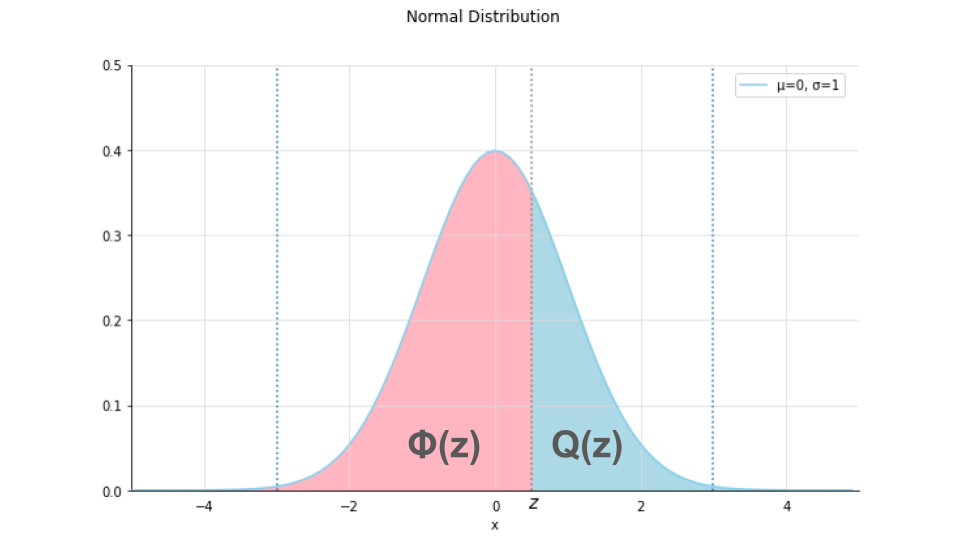
上式の$Q(z)$は標準正規分布の上側確率です。
$Q(z)$hは下図の青の部分であり、下図のピンクの部分が$\Phi(z)$にあたります。
$\tau$は何を表すのか
$\tau$は、今回の問題においてチェックすべき(検定)統計量を表します。
上記図における$Q(z)$や$\Phi(z)$が標準正規分布に基づいて考えられているように、検定に用いる統計量は標準化される必要があります。
平均$\mu$、標準偏差$\sigma^2$、標本数$n$の正規分布の標本平均$\bar{X}$を標準化する際は、以下のような式を使用します。
$$Z= \frac{(\bar{X}-\mu)}{\sqrt{\frac{\sigma^2}n}} = \frac{\sqrt{n}(\bar{X} – \mu)}{\sigma}$$
上式は、標本平均を標本平均の期待値$E(\bar{X})$と分散$V(\bar{X})$を使用して標準化しています。
$$E(\bar{X}) = E\left(\frac{\sum^n X_i}n\right) = \frac{E\left(\sum^n X_i\right)}n = \frac{\sum^n E(X_i)}n = \frac{n\mu}n = \mu$$
$$V(\bar{X}) = V\left(\frac{\sum^n X_i}n\right) = \frac{\sum^nV\left( X_i\right)}{n^2} = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}n$$
今回の問題においても、標本平均$\bar{X}$と$\bar{Y}$を使用して標準化を行なっています。
$$E(\bar{X}-\bar{Y}) = E\left(\frac{\sum^m X_i}{m}\right) – E\left(\frac{\sum^n Y_i}{n}\right) = \mu_1 – \mu_2$$
$$ V(\bar{X} – \bar{Y}) = V(\bar{X}) + V(\bar{Y}) = \frac{\sigma_0^2}m + \frac{\sigma_0^2}n = \left(\frac1m + \frac1n\right)\sigma_0^2 = \frac{(m + n)\sigma_0^2}{mn}$$
よって、標準化された検定統計量は
$$\tau = \frac{\mu_1 – \mu_2}{\sqrt{\frac{(m+n)\sigma_0^2}{mn}}} = \sqrt{\frac{mn}{(m+n)}}\frac{(\mu_1 – \mu_2)}{\sigma_0}$$
なぜ$\Phi(z_{\alpha})$ではなく、$\Phi(z_{\alpha}-\tau)$なのか
2つ前のCheckによれば、標準正規分布の点$z$における累積分布は$\Phi(z)$で求められるとのことでした。
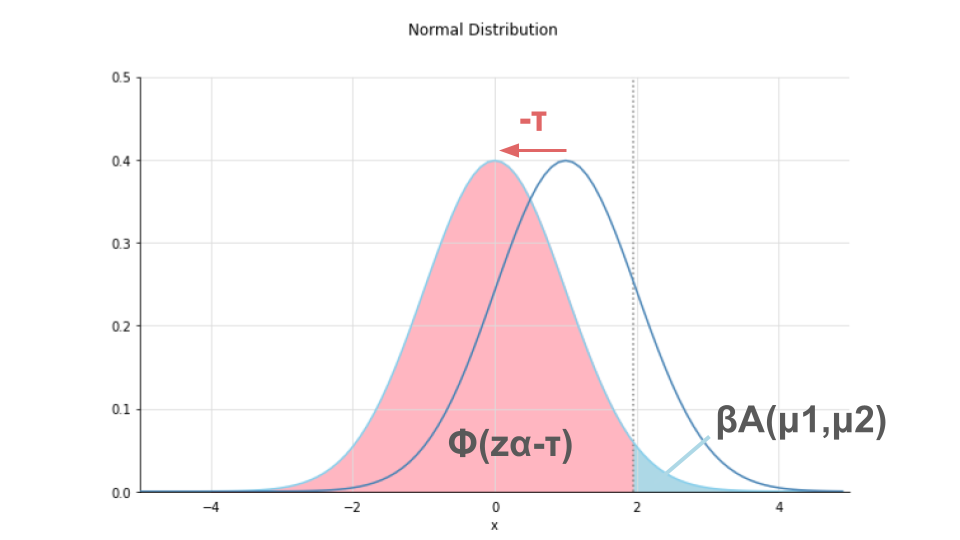
今回の問題では、なぜ$\Phi$の中が$z_{\alpha}$(=有意水準$\alpha$である時の累積分布)ではなく、$z_{\alpha} – \tau$なのでしょうか。
それは、標準正規分布からずれている分を$\tau$によって補正しているためです。
標準正規分布は平均が$\mu$ですが、今回考えている2つの標本の差の正規分布は検定統計量$\tau$の分だけずれてしまっています。
そのずれた分$\tau$を補正することによって、標準正規分布と同様の方法で累積分布を求めているのです。
コード
今回の問題は以下のPythonコードによって解くことができます。
import numpy as np
import math
from scipy.stats import norm
# τを求める関数
def def_tau(m, n, mu_diff, sigma):
tau = math.sqrt(m * n / (m + n)) * (mu_diff) / sigma
return tau
# 片側検定の時の検出力を求める関数
def beta_aside(alpha, m, n, mu_diff, sigma):
tau = def_tau(m, n, mu_diff, sigma)
# 有意水準に基づいて、帰無仮説を棄却する時のzの最低ラインを求める(パーセント・ポイント関数)
ppf = norm.ppf(1 - alpha)
# τを使って補正を行い、累積分布を求める
cdf = norm.cdf(ppf - tau)
# 1 - 累積分布によって、検定力を求める
beta = 1 - cdf
return beta
# 両側検定の時の検出力を求める関数
def beta_bothside(alpha, m, n, mu_diff, sigma):
tau = def_tau(m, n, mu_diff, sigma)
# 有意水準に基づいて、帰無仮説を棄却する時のzの最低ラインを求める
ppf = norm.ppf(1 - alpha/2)
# τを使って補正を行い、上側の累積分布と下側の累積分布を求める
upper_cdf = norm.cdf(ppf - tau)
lower_cdf = norm.cdf(-ppf - tau)
# 1 - 上側の累積分布 + 下側の累積分布によって、検定力を求める
beta = 1 - upper_cdf + lower_cdf
return beta
# 設定
m = 5
n = 5
mu_diff = 1
sigma = 1
alpha = 0.05
aside_beta = beta_aside(alpha = alpha, m = m, n = n, mu_diff = mu_diff, sigma = sigma)
print(f"片側検定におけるbetaの値: ", aside_beta)
bothside_beta = beta_bothside(alpha = alpha, m = m, n = n, mu_diff = mu_diff, sigma = sigma)
print(f"両側検定におけるbetaの値: ", bothside_beta)解説
今回の問題は上記コードによって、3つのステップで解くことができています。
- $\tau$を求める関数を定義する
- 片側検定、両側の検定の際の検定力を求める関数を定義する
- $m,n,\mu_1-\mu_2,\sigma_0,\alpha$の具体的な値を代入する
順を追って解説していきます。
$\tau$を求める関数を定義する
まずは$\tau$を求める関数を定義します。
今回の場合は$\mu_1-\mu_2$という方で引数を与えましたが、具体的な$\mu_1,\mu_2$で検討を行いたい場合は適宜関数を修正してください。
# τを求める関数
def def_tau(m, n, mu_diff, sigma):
tau = math.sqrt(m * n / (m + n)) * (mu_diff) / sigma
return tau片側検定、両側の検定の際の検定力を求める関数を定義する
片側検定、両側検定の際の検定力を求める関数を定義します。
関数内部では以下のような処理をしています。
- $\tau$を求める
- 有意水準($=Q(z)$の値)に基づいて、帰無仮説を棄却する時の$z$の最低ラインを求める
- 検定力を$1-累積分布=Q(z)$で求める
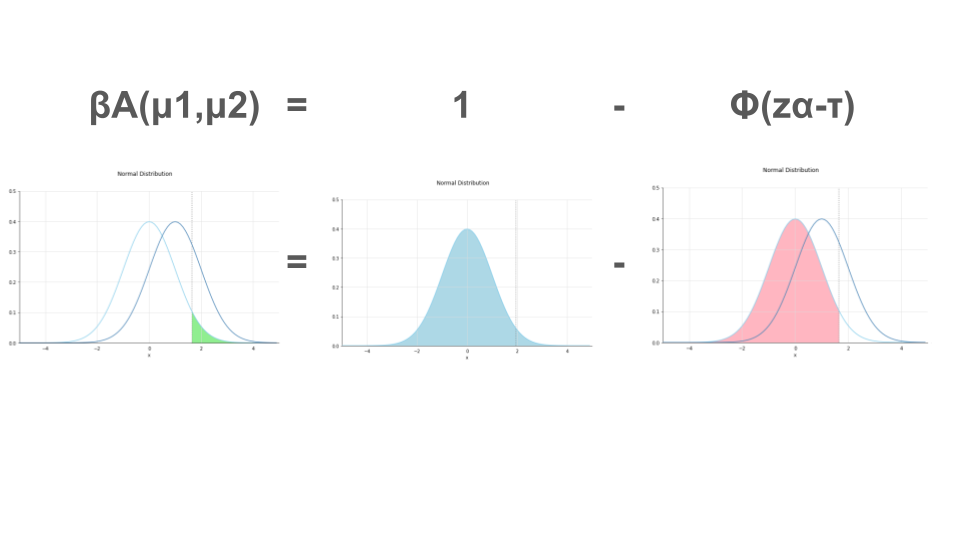
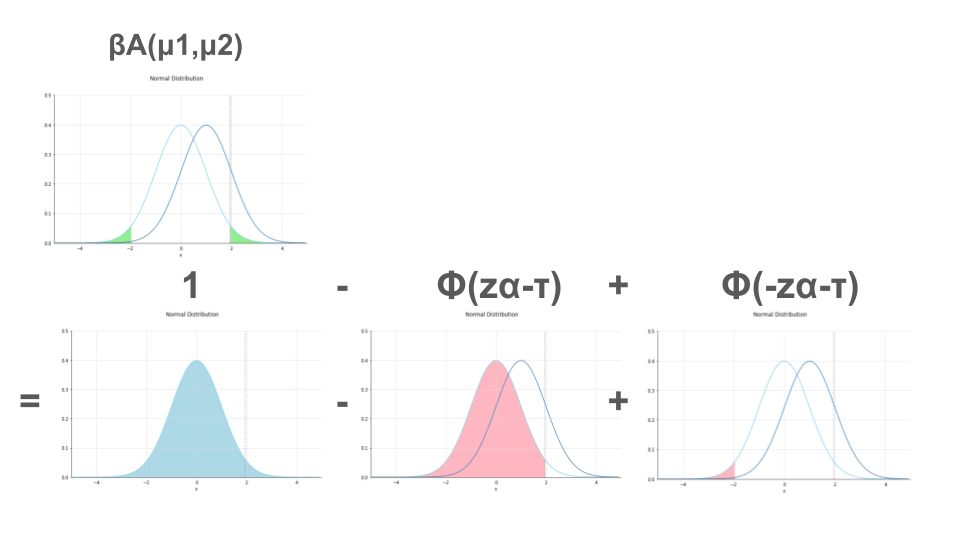
なお、片側検定、両側検定における検定力を導出する式のイメージは以下の通りです。
# 片側検定の時の検出力を求める関数
def beta_aside(alpha, m, n, mu_diff, sigma):
tau = def_tau(m, n, mu_diff, sigma)
# 有意水準に基づいて、帰無仮説を棄却する時のzの最低ラインを求める(パーセント・ポイント関数)
ppf = norm.ppf(1 - alpha)
# τを使って補正を行い、累積分布を求める
cdf = norm.cdf(ppf - tau)
# 1 - 累積分布によって、検定力を求める
beta = 1 - cdf
return beta
# 両側検定の時の検出力を求める関数
def beta_bothside(alpha, m, n, mu_diff, sigma):
tau = def_tau(m, n, mu_diff, sigma)
# 有意水準に基づいて、帰無仮説を棄却する時のzの最低ラインを求める(パーセント・ポイント関数)
ppf = norm.ppf(1 - alpha/2)
# τを使って補正を行い、上側の累積分布と下側の累積分布を求める
upper_cdf = norm.cdf(ppf - tau)
lower_cdf = norm.cdf(-ppf - tau)
# 1 - 上側の累積分布 + 下側の累積分布によって、検定力を求める
beta = 1 - upper_cdf + lower_cdf
return beta$m,n,\mu_1-\mu_2,\sigma_0,\alpha$の具体的な値を代入する
ここまでで検定力の計算に必要な関数の定義は完了したので、具体的な値を代入して検定力を求めていきます。
# 設定
m = 5
n = 5
mu_diff = 1
sigma = 1
alpha = 0.05
aside_beta = beta_aside(alpha = alpha, m = m, n = n, mu_diff = mu_diff, sigma = sigma)
print(f"片側検定におけるbetaの値: ", aside_beta)
bothside_beta = beta_bothside(alpha = alpha, m = m, n = n, mu_diff = mu_diff, sigma = sigma)
print(f"両側検定におけるbetaの値: ", bothside_beta)
おまけ:平均の差の違いによる検定力の違いを可視化してみる
今回の問題においては、2つの正規分布の標本平均の差が1である場合についての検定力を求めていきましたが、2つの正規分布の標本平均の差を動かした時に検定力がどのように変わるのかについて可視化してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# 平均の差のリストを準備
mu_diff = np.linspace(-5,5, 1000)
beta = beta_bothside(alpha = alpha, m = m, n = n, mu_diff = mu_diff, sigma = sigma)
plt.plot(mu_diff, beta)
plt.axhline(bothside_beta, c = 'gray', ls = 'dotted')
plt.axvline(1, c = 'b', ls = 'dotted')
plt.ylabel('Power Function')
plt.xlabel(r'$\mu_1 - \mu_2$')上記コードでは2つの正規分布の標本平均の差を-5から5まで動かした時の両側検定における検定力を求めて可視化を行なっています。
点線がクロスしている部分が今回の演習問題において求めた検定力です。
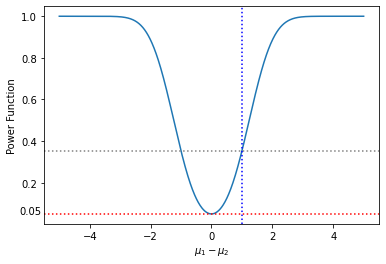
上図のように可視化をしてみると、以下のようなことがわかります
- 標本平均の差が2以上開くと90%の検定力で標本平均の差を検出できる
- 標本平均に差がない(=帰無仮説が棄却されない)確率は有意水準5%と一致する
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第6章-演習問題2「母平均についての2標本問題」を、Pythonを使って解く方法について、解法の手順を含めて解説いたしました。
また、おまけコンテンツとして、標本平均の差を自由に動かした際の検定力についても可視化を行いました。
「自然科学の統計学」における検定力の章は少し難解でわかりづらいですが、要は標準化して累積分布(または上側確率)を上手いこと使って帰無仮説を棄却する時の確率を求める、ということを抑えていれば応用は可能かと思われます。
皆さんもぜひ平均値や分散の検定をPythonで行なってみてください!



コメント