
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題1「線形確率モデルとの比較」をPythonで解いていきたいと思います。
今回の問題は非常にシンプルな単回帰モデルの構築なので、かなり理解いただきやすいかと思われます。
問題文
<線形確率モデルとの比較>
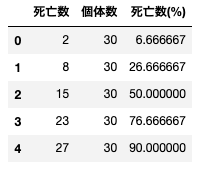
i ) 線形確率モデルを用いて、以下表の量・反応関係を記述する$\alpha_0,~\alpha_1$と求めよ
ii ) この推定値$\hat{\alpha_0},~\hat{\alpha_1}$を用いて、死亡確率$P_i$を投与量別に推定せよ
iii ) 以下表の投与量別推定死亡確率$\hat{P_i}$をグラフにプロットし、ii )の結果を加えて書き入れよ
iv ) この線形確率モデルで、$\hat{P_i} > 1$ また $\hat{P_i} < 0$となる$X_i$の範囲を求めよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第8章 演習問題 P249
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
実装コード
今回の解答に使用するコードは以下のとおりです。
なお、(iv)については手計算をしております。
# 基本的なライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
df = pd.read_csv('Log_Concentration_by_Individual_Case_Death_Survival.csv')
X = df[['Xi']]
y = df[['Yi']]
# 単回帰モデル構築
model_lr = LinearRegression()
model_lr.fit(X, y)
# (1)
print('線形関数の切片 a0: %.4f' %model_lr.intercept_)
print('線形関数の回帰変数 a1: %.4f' %model_lr.coef_)
print('y= %.4f + %.4fx' % (model_lr.intercept_ , model_lr.coef_))
# (2)
print(f'X = {0}の時、Pi = {model_lr.predict([[0]])[0][0]}')
print(f'X = {1}の時、Pi = {model_lr.predict([[1]])[0][0]}')
print(f'X = {2}の時、Pi = {model_lr.predict([[2]])[0][0]}')
print(f'X = {3}の時、Pi = {model_lr.predict([[3]])[0][0]}')
print(f'X = {4}の時、Pi = {model_lr.predict([[4]])[0][0]}')
#(3)
df2 = pd.read_csv('Probability_of_death_by_dose_from_probit_logit_model.csv')
display(df2)
plt.figure(figsize = (8,8))
plt.scatter(df2.index, df2['プロビット'], label = 'Probit')
plt.scatter(df2.index, df2['ロジット'], label = 'Logit')
plt.scatter(df2.index, df2['データ'], label = 'Data')
# 線形確率モデルの予測値作成
X = [0,1,2,3,4]
preds = [ model_lr.predict([[i]]) for i in X]
plt.scatter(df2.index, preds, color = 'pink', label = 'Pred')
plt.legend()(i)の解説
# 基本的なライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
df = pd.read_csv('Log_Concentration_by_Individual_Case_Death_Survival.csv')
X = df[['Xi']]
y = df[['Yi']]
# 単回帰モデル構築
model_lr = LinearRegression()
model_lr.fit(X, y)
# (1)
print('線形関数の切片 a0: %.4f' %model_lr.intercept_)
print('線形関数の回帰変数 a1: %.4f' %model_lr.coef_)
print('y= %.4f + %.4fx' % (model_lr.intercept_ , model_lr.coef_))(i)の前提として、先ほどの死亡数/個体数に関するデータフレームから、$X_i$に投与量を、$Y_i$に死亡したか否かの二値を入力したデータフレームを作成しております。
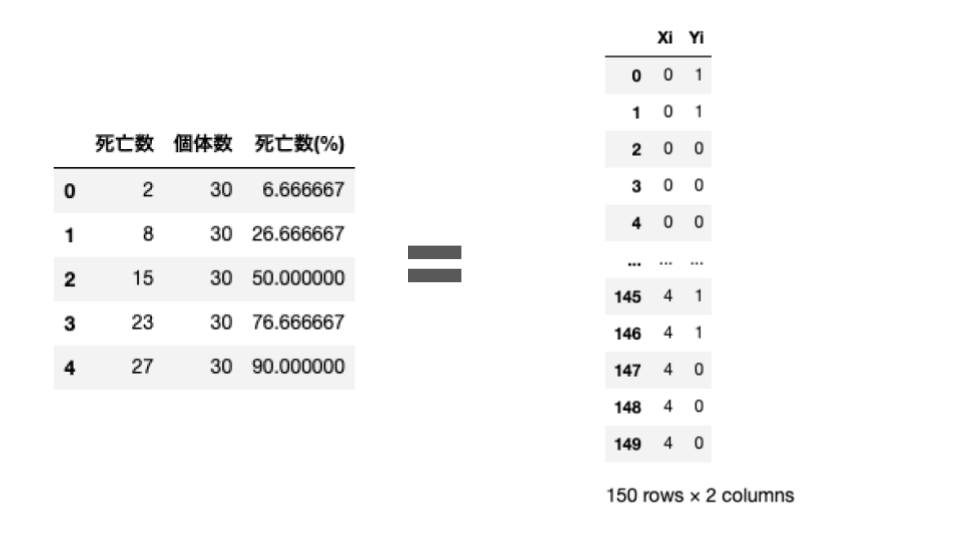
このデータフレームをsklearnの線形回帰モデルLinearRegressionにつっこんで、出力を見れば$\alpha_0,~\alpha_1$の値を知ることができます。

(ii)の解説
# (2)
print(f'X = {0}の時、Pi = {model_lr.predict([[0]])[0][0]}')
print(f'X = {1}の時、Pi = {model_lr.predict([[1]])[0][0]}')
print(f'X = {2}の時、Pi = {model_lr.predict([[2]])[0][0]}')
print(f'X = {3}の時、Pi = {model_lr.predict([[3]])[0][0]}')
print(f'X = {4}の時、Pi = {model_lr.predict([[4]])[0][0]}')先ほど作成した線形回帰モデルmodel_lrのpredictメソッドを使用して、投与量別の死亡確率$P_i$を推定します

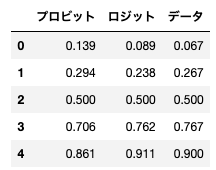
(iii)の解説
#(3)
df2 = pd.read_csv('Probability_of_death_by_dose_from_probit_logit_model.csv')
display(df2)
plt.figure(figsize = (8,8))
plt.scatter(df2.index, df2['プロビット'], label = 'Probit')
plt.scatter(df2.index, df2['ロジット'], label = 'Logit')
plt.scatter(df2.index, df2['データ'], label = 'Data')
# 線形確率モデルの予測値作成
X = [0,1,2,3,4]
preds = [ model_lr.predict([[i]]) for i in X]
plt.scatter(df2.index, preds, color = 'pink', label = 'Pred')
plt.legend()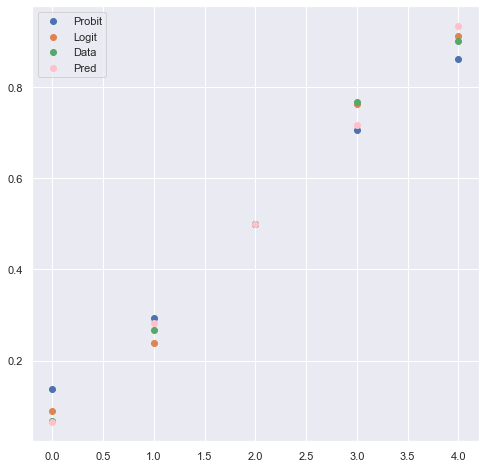
上記グラフを見ると、ロジットモデルが最もよくデータを再現しており、次点で線形回帰モデル、最後がプロビットモデルであることがわかります。
(iv)の解説
線形確率モデルにおいて$\hat{P_i} > 1$となるのは
$$ 0.0667 + 0.2167x > 1$$
$$ 0.2167x > 0.9333$$
$$x > 4.3068758652515$$
同様に$\hat{P_i} < 0$となるのは
$$ 0.0667 + 0.2167x < 0$$
$$ 0.2167x < -0.0667$$
$$ x < -0.30779880018458694$$
上記のように、プロビットモデルよりも当てはまりが良かったとしても、データによっては線形確率モデルは確率0未満または確率1以上という説明不可能な値を取ってしまうことがあります。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題1「線形確率モデルとの比較」をPythonで解いていきました。
今回の可視化によって、線形回帰モデルはプロビットモデルやロジットモデルよりも良い推定を行う可能性はありますが、確率0未満または確率1以上のような確率として不適合な値を推定してしまう可能性があるため、質的データの予測確率としてはあまり利用されることがない、というのがお分かりいただけたでしょうか?
皆さんも、目的変数の特性やデータの特性によって、どのようなモデルを構築するのが尤もらしいのかを検討いただけると幸いです!




コメント