
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題6「ブラッドリー・テリーのモデル」にPythonを適用して問題を解いていきたいと思います。
今回実装するPythonコードの詳細については別記事で紹介しているので、本記事では実装コードと結果について簡単に共有させていただきます!
問題文
<ブラッドリー・テリーのモデル>
下表は1991年度プロ野球セ・リーグ勝敗表である。$K=100$として、本文で述べた方法により各チームの強さ$\theta$を推定し、モデルの当てはまりの良さを$\chi^2$適合度検定を用いてチェックせよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 演習問題 P175~176
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
実装コード
本問題を解くための実装コードは以下の通りです。
import numpy as np
import pandas as pd
df = pd.read_csv('Bradley_Terrys_Model.csv', index_col = 0)
display(df)
# チームまたは選手数を取得
N = len(df)
# 全チームの強さの合計値を決定
K = 100
# 初期thetaを決定
thetas = [ K/N for _ in range(N)]
print('初期theta:', thetas)
def calc_bradly(thetas, dataframe):
# 元の強さold_thetasと新しい強さthetasの差が0.000001未満に収束するまで続ける
while True:
old_thetas = thetas.copy()
for i in range(len(thetas)):
# 式①を計算するための変数sum_
sum_ = 0
for j in range(len(thetas)):
# 同じチーム同士の場合はpass
if i == j:
pass
else:
# (対戦試合数)/(2チームの強さの和)
sum_ += (df.iloc[i, j] + df.iloc[j, i]) / (thetas[i] + thetas[j])
print(f"({i},{j}) : {sum_}")
# チームiの総勝利数を計算
y_sum = df.iloc[i, :].sum()
# 強さthetaを更新
thetas[i] = y_sum / sum_
# 元の強さold_thetasと新しい強さthetasの差を計算
diff = np.abs(np.array(old_thetas) - np.array(thetas)).sum()
print('diff = ', diff)
if abs(diff) <= 0.0000001:
# 収束した時のthetas
print("収束")
return thetas
else:
# 合計が100になるように標準化
thetas = thetas / np.sum(thetas)
thetas *= 100
print('thetas: ', thetas)
thetas = calc_bradly(thetas, df)
print(thetas)
# 推定結果を入れるためのDataFrameの作成
tmp = pd.DataFrame(index = df.columns, columns =df.columns)
for i in range(N):
for j in range(N):
if i == j:
pass
else:
# 2つのチームの合計試合数
sum_ = df.iloc[i, j] + df.iloc[j, i]
# ブラッドリー・テリーのモデル
p = thetas[i] / (thetas[i] + thetas[j])
# 勝ち数を推定
tmp.iloc[i, j] = p * sum_
display(tmp)
display(df)
import scipy.stats as sps
import math
chi = 0
for i in range(N):
for j in range(N):
if i == j:
pass
else:
real = df.iloc[i, j]
inf = tmp.iloc[i, j]
chi += (real - inf)**2 / inf
print("カイ2乗値: ", chi)
v = math.comb(N -1, 2)
if sps.chi2.ppf(q = 0.99, df = v) <= chi:
print('1%で統計的に有意であり、ブラッドリー・テリーのモデルは適合しない')
elif sps.chi2.ppf(q = 0.95, df = v) <= chi:
print('5%で統計的に有意であり、ブラッドリー・テリーのモデルは適合しない')
else:
print('5%で統計的に有意でなく、ブラッドリー・テリーのモデルは適合する')本コードの詳細な解説については以下記事をご覧ください
本コードを実行すると、$\eps < 10^{-7}$のオーダーで収束したのちに、以下のように各チームの強さパラメータを得ることができます。

この$\theta$の値は教科書の模範回答とほとんど一致しています。
差異があるのは、今回実装したプログラムの方が小数点以下のかなりの桁数まで計算を行うことができるからです。
また、ブラッドリー・テリーのモデルを仮定した場合の$\chi^2$値は約$6.841$となり、自由度$[}_5\mathrm{C}_2 = 10$、有意水準5%の$\chi^2$分布$\chi^2_{0.05}(10)=18.307$より小さく、ブラッドリーテリーのモデルは今回のデータによく適合していることがわかります。

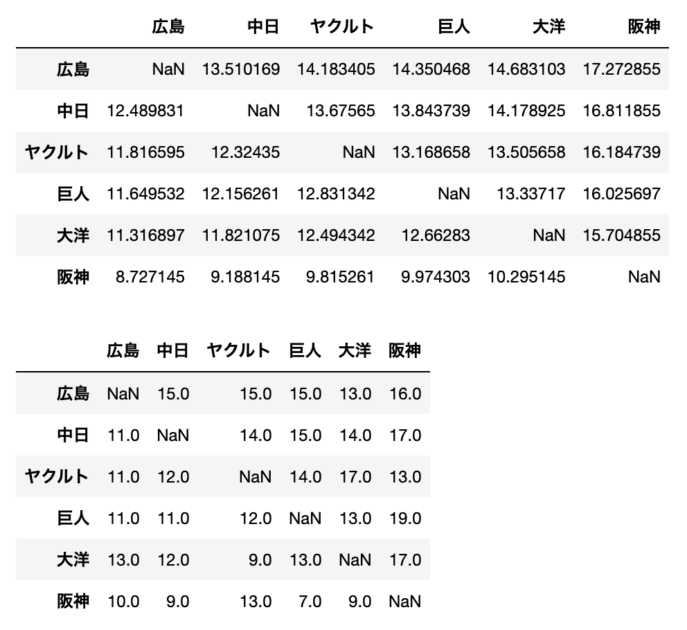
実際にブラッドリー・テリーのモデルから算出した強さ$\theta$を用いて各チームの勝率の理論値を算出しましたが、元の勝敗表とよく一致していることがわかります。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題6「ブラッドリー・テリーのモデル」にPythonを適用して問題を解く方法について、実装コードを紹介しながら出力結果を簡単に解説いたしました。
詳細な解説については別の記事に譲りますが、今回のセ・リーグのデータではブラッドリー・テリーのモデルがよく適合することを示すことができました。
なお、元の解説記事においては、ブラッドリー・テリーのモデルがよく適合しないパターンの$\chi^2$値を見ることができます。
みなさんも勝敗の関係にある程度の線形な関係($A<B<C$)が認められるような場合には、ブラッドリー・テリーのモデルを使って、強さ$\theta$というパラメータを求めてみましょう!





コメント