
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」に登場する、チーム間の勝敗を計算するモデル「ブラッドリー・テリーのモデル(Bradly-Terry’s model)」によるチームの強さの推定をPythonで実装してみたので、実装の中身について紹介いたします。
このプログラムは$N\times N$の勝敗表があれば、それぞれのチームの強さを数値で求めることができ、なおかつ2つのチームが対戦した場合の勝率についても理論的に計算することができますので、チーム間の勝率を計算してみたい方はぜひご活用ください!
ブラッドリー・テリーのモデルとは
ブラッドリー・テリーのモデルとは、簡単にいえばチームや個人の「強さ」を数値化するためのモデルです。
例えば、以下のような1981年パ・リーグの勝敗表があったとします。
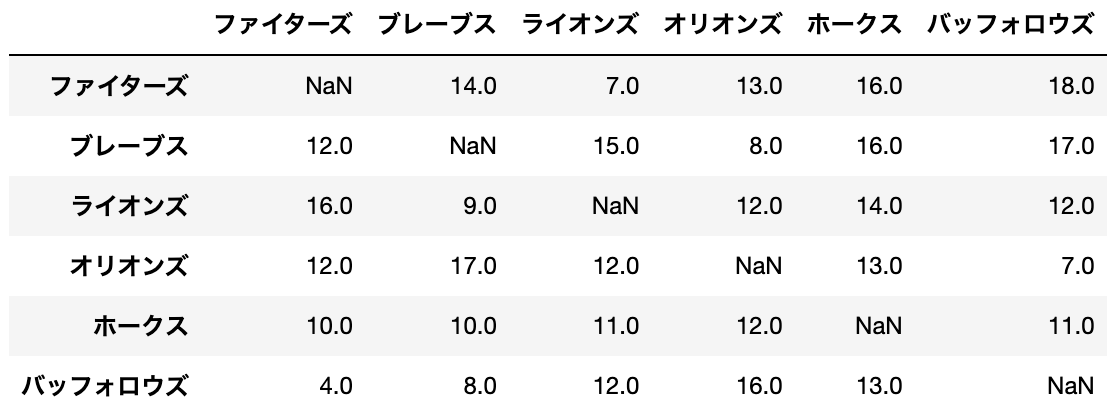
ブラッドリー・テリーのモデルとは、このような勝敗表をもとに各チームの強さ$\theta_i$の値を求めるための数理モデルです。
ブラッドリー・テリーのモデルに基づいて計算を進めていくと、
$$ ファイターズの強さ\theta_1 = 19.9$$
$$ ブレーブスの強さ\theta_2 = 18.8$$
のように各チームの値が求まります。
すると、この値を使って以下のように勝率を求めることができます。
ファイターズがブレーブスに勝つ確率を$p_{12}$、ブレーブスがファイターズに勝つ確率を$p_{21}4とします。
$$ p_{12} = \frac{\theta_1}{\theta_1 + \theta_2} = \frac{19.9}{19.9+18.8} = 0.5153$$
$$ p_{21} = \displaystyle\frac{\theta_2}{\theta_1 + \theta_2} = \frac{18.8}{19.9+18.8} = 0.4847 $$
上記の式のように、チーム1の勝率を求めるときに、チーム1の強さ$\theta_1$を2つのチームの強さの和$\theta_1 + \theta_2$で割って求めるような理論モデルをブラッドリー・テリーのモデルと呼びます。
次に、勝敗表とブラッドリー・テリーのモデルを使用し、各チームの強さというパラメータを求める実装コードを紹介いたします。

ブラッドリー・テリーのモデルの実装コード
今回は上記例の1981年のパ・リーグの勝敗表を使用します。
df = pd.read_csv('Pacific_League_Winners_and_Losers_Chart.csv', index_col = 0)
display(df)「自然科学の統計学」に登場するデータについては以下記事からダウンロードすることができます。
ブラッドリー・テリーのモデルから各チームの強さを求めるコードは以下のとおりです。
# チームまたは選手数を取得
N = len(df)
# 全チームの強さの合計値を決定
K = 100
# 初期thetaを決定
thetas = [ K/N for _ in range(N)]
print('初期theta:', thetas)
def calc_bradly(thetas, dataframe):
# 元の強さold_thetasと新しい強さthetasの差が0.000001未満に収束するまで続ける
while True:
old_thetas = thetas.copy()
for i in range(len(thetas)):
# 式①を計算するための変数sum_
sum_ = 0
for j in range(len(thetas)):
# 同じチーム同士の場合はpass
if i == j:
pass
else:
# (対戦試合数)/(2チームの強さの和)
sum_ += (df.iloc[i, j] + df.iloc[j, i]) / (thetas[i] + thetas[j])
print(f"({i},{j}) : {sum_}")
# チームiの総勝利数を計算
y_sum = df.iloc[i, :].sum()
# 強さthetaを更新
thetas[i] = y_sum / sum_
# 元の強さold_thetasと新しい強さthetasの差を計算
diff = np.abs(np.array(old_thetas) - np.array(thetas)).sum()
print('diff = ', diff)
if abs(diff) <= 0.0000001:
# 収束した時のthetas
print('収束')
return thetas
else:
# 合計が100になるように標準化
thetas = thetas / np.sum(thetas)
thetas *= K
print('thetas: ', thetas)
thetas = calc_bradly(thetas, df)
print(thetas)上記のコードを実行すると、以下の手順で勝敗表から最も当てはまりがいい各チームの強さ$\theta$を計算してくれます。
- 初期$\theta$を算出する
- あるチームに対して、各対戦チームごとに(対戦試合数)/(2チームの強さ$\theta$の和) を計算して、強さ$\theta$を更新する
- 更新後の強さ$\theta$と更新前の強さ$\theta$の差が0.0000001以下になるまで上記を繰り返す
- 繰り返しをする際には全てのチームの強さの合計が任意の値$K$になるように調整する


ブラッドリー・テリーのモデルと実装の解説
ここからはブラッドリー・テリーのモデルの理論面と実装との対応関係について理解を深めたい方に向けて解説をしていきます。
チーム1 vs チーム2の勝率の分布: 二項分布
野球のような勝負の世界では、そのチームや個人の持つ強さ$\theta$という変数が非常に重要な意味を持ちます。
つまり、朝倉未来とデータサイエンティストの僕が戦っても、100戦100敗することが決まっているように、それぞれのチーム/個人の持つ強さ$\theta$によって勝敗は決定されます。
一方で、巨人と阪神のように強さが圧倒的に異なるとはいえないような場合には、強さ$theta$が重要には変わりないものの、時には巨人が勝ち、時には阪神が勝つというような一種の確率的な挙動を見せることがあります。
ここで、高校数学の復習を挟みましょう。
ここに均一なコイン、つまり表が出る確率も裏が出る確率もともに50%であるようなコインがあるとします。
均一なコインをn回投げる時のk回表が出る確率$f(k)$は以下のように表すことができます。
$$ f(k) = {}_n \mathrm{C}_k \left( \frac12\right)^k\left( \frac12\right)^{n-k}$$
上記のような確率$f(x)$によって、10回中5回表が出る確率や10回中2回表が出る確率が決まってきます。
つまり、$k = \{1,~2,~\cdots,~9,~10\}$の値において、それぞれ確率$f(1), ~f(2), ~\cdots,~f(9),~f(10)$を求めることができます。
上記のようなそれぞれの値$k$における確率$f(k)$のことを確率分布と呼び、コイン投げのような「表か裏か」「勝ちか負けか」のような2つの事柄の起こりやすさを表す確率を二項分布と呼びます。
さて、野球の話に戻りましょう。
それぞれの変数を以下のように定義します。
- チーム1がチーム2に勝つ確率$p_{12}$
- チーム2がチーム1に勝つ確率$p_{21}$
- チーム1がチーム2に実際に勝った回数$y_{12}$
- チーム2がチーム1に実際に勝った回数$y_{21}$
上記のように定義すると、チーム1がチーム2に$y_{12} + y_{21}$回の試合のうち、$y_{12}$回勝つ確率は以下のような二項分布になると考えられます。
$$ P(Y_{ij}=y_{12})={}_{y_{12} + y_{21}}\mathrm{C}_{y_{12}}(p_{12})^{y_{12}}(p_{21})^{y_{21}}$$
さて、上記の式ではチーム1のチーム2に対する勝率について計算しましたが、今度は全チームの勝率の確率分布を考えていきましょう。
チーム1とチーム2の勝敗は他のチームの勝敗に影響を及ぼさない: 独立試行
ここで、再度コインの例に立ち返りましょう。
$n$回のコイン投げの試行のうち、$k$回表が出る確率は以下のような式で表されました。
$$ f(k) = {}_n \mathrm{C}_k \left( \frac12\right)^k\left( \frac12\right)^{n-k}$$
上記の式のうち、$\left(\frac12\right)^k$の部分は表が出る確率$\frac12$を$k$回分かけ算をしていることになります。
このかけ算がOKな理由は、1回目コインを投げる時の表が出る確率は$\frac12$だし、2回目や3回目にコインを投げた時に表が出る確率もまた$\frac12$という、コインを投げるという試行の独立性に基づいています。
つまり、すごくざっくりいうと、影響を及ぼさない試行同士の確率はかけ算してOK、ということです。

確率が分からないから実際の値からいい感じの確率を求めたい: 尤度
ここからの説明は、多少理論的厳密性を犠牲にして、理解いただきやすいようにいたしますので、ご了承いただけると幸いです。
均一なコイントスの例では、表が出る確率が$\frac12$と分かっていたため、10回中5回表が出る確率を式に$n=10,~k=5,~p=\frac12$を代入して求めることができます。
一方で、野球の例で言えば、それぞれのチームが勝つ確率$p$と、確率を計算するために必要な各チームの強さ$\theta_{i}$はこれから求めたいと考えているものです。
それでは、どのようにして確率$p$ないし強さ$\theta_i$を求めればいいのでしょうか。
ここで活用する概念が尤度(ゆうど)と呼ばれるものです。
尤度の「尤」は「尤もらしい(=もっともらしい)」と読み、要するに「それっぽい値」という意味になります。
そして、この尤度(という確率)が最も高くなる時の$\theta$の値が、「それが一番可能性高くね?」と言える$\theta$の値なわけです。
つまり、これからやりたいことは勝敗表の各チームの勝敗というすでに観測された値から尤度が最大になるような強さ$\theta_i$を求めようぜ、ということです。
その手法は大きく分けて4つのステップを取り、最終ステップが本記事で実装したコードの部分になります。
なお、ステップ1で全てのチームの勝敗の確率をかけ算してOKな理由は、他のチームの勝敗は自分たちのチームの勝敗に影響を及ぼさないからです。
- 全てのチームの勝敗の確率を全てかけ算して尤度$L(p)$とする
- $L(p)$のままだと計算しづらいので自然対数$\log$をとり、$\log{L(p)}$とする
- 尤度が最大になる時の$\theta$の値を求めるために、$\log{L(p)}$を偏微分して、各チームの強さ$\theta_i$を推定する式を立てる
- 各チームの強さ$\theta_i$を推定する式を使って順々に各チームの強さを推定するのをたくさん繰り返し、変化がなくなった時の値を最終的な強さとする(コード実装部分)
$\theta_i$を推定する式を求める計算過程は以下のとおりです。
興味のある方はご確認ください。
全てのチームの勝敗の確率を全てかけ算して尤度$L(p)$とする
$n$は総チーム数とします
$$ L(p) = \prod_{1 \leqq i }\prod_{< j \leqq n} {}_{y_{ij} + y_{ji}}\mathrm{C}_{y_{ij}}(p_{ij})^{y_{ij}}(p_{ji})^{y_{ji}}$$
$L(p)$のままだと計算しづらいので自然対数$\log$をとり、$\log{L(p)}$とする
チーム$i$がチーム$j$に勝つ確率を$p_{ij} =\frac{\theta_{ij}}{\theta{ij} + \theta{ji}}$というブラッドリー・テリーのモデルで定義し、$L(p)$に代入した上で自然対数$\log{L(p)}$を計算すると以下のようになります。
ここで、$r_{ij} = y_{ij} + y_{ji}$(=2つのチームの総試合数)、$y_{i\cdot} = y_{i1} + \cdots + y_{in}$(=チーム$i$の総勝利数)です。
$$ \log{L(p)} =\sum_{1 \leqq i }\sum_{< j \leqq n} \{ \log{{}_{r_{ij}} \mathrm{C}_{r_{ij}}} – r_{ij} \log{(\theta_i + \theta_j)}\} \sum_{i} y_{i\cdot}\log{\theta_i}$$
$\log{L(p)}$を偏微分して、各チームの強さ$\theta_i$を推定する式を立てる
直前の式を$\theta_i$で偏微分して0とおき、式変形をすると次のような式が得られます。
$$ \theta_i \sum_{j(\neq i)} \frac{r_{ij}}{\theta_i + \theta_j} = y_{i\cdot} $$
これにより、各チームの強さの推定値$\theta_i$を以下の式で求めることができます。
$$ \hat{\theta_i} = \frac{y_{i\cdot}}{\sum_{j(\neq i)}\frac{r_{ij}}{\theta_i + \theta_j}}$$
ここで、一番最初の$\theta_i$推定時には、右辺の$\theta_{i},~\theta_{j}$には適当な初期値(実装コードでは$\frac{K}{N}$)が入ります。
$\sum_{j(\neq i)}\frac{r_{ij}}{\theta_i + \theta_j}$を求める部分が実装コードの以下になります。
# (対戦試合数)/(2チームの強さの和)
sum_ += (df.iloc[i, j] + df.iloc[j, i]) / (thetas[i] + thetas[j])$y_{i\cdot}$を求める部分が実装コードの以下の部分になります。
# チームiの総勝利数を計算
y_sum = df.iloc[i, :].sum()強さの推定値$\theta_i$を求める部分が実装コードの以下の部分になります。
# 強さthetaを更新
thetas[i] = y_sum / sum_各チームの強さ$\theta_i$を推定する式を使って順々に各チームの強さを推定するのをたくさん繰り返し、変化がなくなった時の値を最終的な強さとする
上記の推定を各チーム分繰り返します。
また、更新前の強さ$\theta_i$と更新後の強さ$\theta_i$の差分は以下のコードで確認しています。
# 元の強さold_thetasと新しい強さthetasの差を計算
diff = np.abs(np.array(old_thetas) - np.array(thetas)).sum()
print('diff = ', diff)
if abs(diff) <= 0.0000001:
# 収束した時のthetas
print('収束')
return thetas
else:
# 合計がK=100になるように標準化
thetas = thetas / np.sum(thetas)
thetas *= K
print('thetas: ', thetas)else以降のコードでは、各チームの強さの合計が100になるように調整をしていますが、今回の計算で関心があるのは各チームの相対的な強さなので、この数字は100でなくても構いません
推定された強さ$\theta$の妥当性の検証
実装コードで推定した各チームの強さ$\theta_i$とブラッドリー・テリーのモデルを用いて、勝ち数を推定すると以下のようになります。
# 推定結果を入れるためのDataFrameの作成
tmp = pd.DataFrame(index = df.columns, columns =df.columns)
for i in range(N):
for j in range(N):
if i == j:
pass
else:
# 2つのチームの合計試合数
sum_ = df.iloc[i, j] + df.iloc[j, i]
# ブラッドリー・テリーのモデル
p = thetas[i] / (thetas[i] + thetas[j])
# 勝ち数を推定
tmp.iloc[i, j] = p * sum_
display(tmp)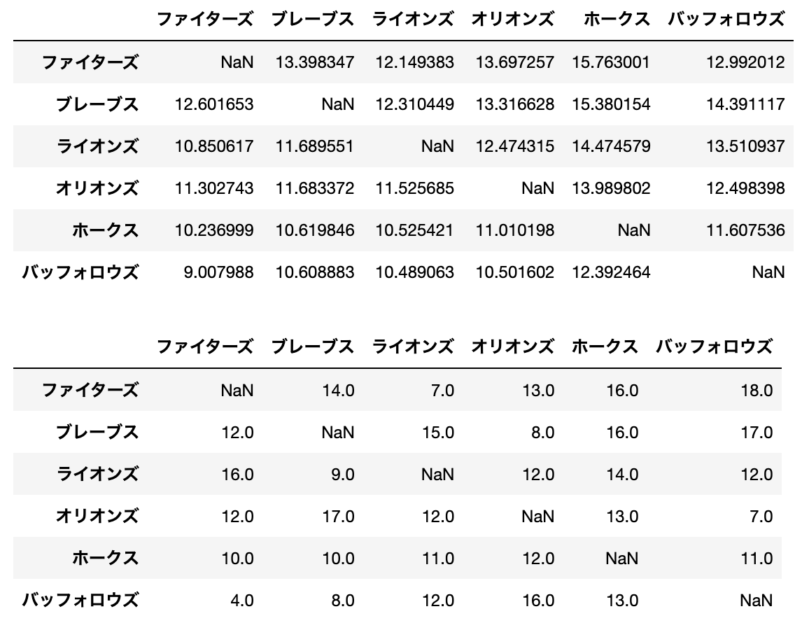
上記の結果より、ある程度当てはまりがいい勝ち数はあるものの、実際の勝ち数とは大きく異なっている推定勝ち数もあることから、スポーツによる勝敗というのは各チームの強さの比較だけでは説明できない要因があることがわかります。
ブラッドリー・テリーのモデルはカイ二乗検定と同様の計算式を使うことによって、モデルと実測値との乖離が許容範囲内かを検証することができます。
# ブラッドリー・テリーのモデルの適合度の検証
import scipy.stats as sps
import math
# カイ2乗値を保存
chi = 0
for i in range(N):
for j in range(N):
if i == j:
pass
else:
# 実測値
real = df.iloc[i, j]
# 推定値
inf = tmp.iloc[i, j]
# (real-inf)**2は実測値と推定値の乖離を表す
chi += (real - inf)**2 / inf
print("カイ2乗値: ", chi)
# 自由度を求める
v = math.comb(N -1, 2)
# カイ2乗分布との比較
if sps.chi2.ppf(q = 0.99, df = v) <= chi:
print('1%で統計的に有意であり、ブラッドリー・テリーのモデルは適合しない')
elif sps.chi2.ppf(q = 0.95, df = v) <= chi:
print('5%で統計的に有意であり、ブラッドリー・テリーのモデルは適合しない')
else:
print('5%で統計的に有意でなく、ブラッドリー・テリーのモデルは適合する')今回のパ・リーグの勝敗については、5%で統計的に有意でないため、ブラッドリー・テリーのモデルを当てはめるのはあまり良くないことがわかります。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」に登場する、チーム間の勝敗を計算するモデル「ブラッドリー・テリーのモデル(Bradly-Terry’s model)」によるチームの強さの推定をPythonで実装し、実装の中身とブラッドリー・テリーモデルの尤度について簡単に解説いたしました!
実装コードは勝敗表のDataFrameまたはCSVさえあれば簡単に実装できるので、気兼ねなくチームの強さを統計的に求めていただけると幸いです!




コメント