時系列データ分析の基礎を学ぶ！時系列データ分析の教科書『経済・ファイナンスデータの計量時系列分析』を読んで得た学び3選

元教師

こんにちは！データサイエンティストの青木和也（https://twitter.com/kaizen_oni）です！

今回の記事では時系列分析の古典的教科書、俗に沖本本とも呼ばれる『経済・ファイナンスデータの計量時系列分析』を読んで得た学びを3つ共有していきたいと思います！

株価の変動や為替レートなど、私たちの日常の様々な場面で見かける時系列データ。

本書はそんな時系列データをモデル化する際に、どのような式を仮定してモデル化すればいいのか、どのような仮定が存在するのかを1から教えてくれる1冊です。

本書の購入を考えている方は本記事を参考に、本書の購入を検討していただけると幸いです！

本書の概要
本書から得た学び
まとめ

本書の概要

本書は経済・ファイナンスデータを計量分析する際に重要な役割を果たす時系列分析の入門書である。
沖本竜義『経済・ファイナンスデータの計量時系列分析』(統計ライブラリー/2010)

本書はデータサイエンス界隈では言わずと知れた時系列分析の名著であり、俗に「沖本本」「緑本」などと言われています。

内容としては、統計的な知識をすでに持っている方が時系列分析について学ぶ際の入門書に位置付けられる1冊であり、

自己相関
定常性
ARMA過程

などの時系列分析における基礎的な内容から

VARモデル
単位根過程
GARCHモデル

などの少し発展的な内容まで、幅広く扱っています。

本書の章立ては以下のとおりです。

時系列分析の基礎概念
ARMA過程
予測
VARモデル
単位根過程
見せかけの回帰と共和分
GARCHモデル
状態変化を伴うモデル

なお、本書には章末に問題がついているので、章の内容を問題で復習をしながら学習を進めることができます。

本書から得た学び

私が本書から得た学びは以下の３点です。

時系列分析でよく目にする「ARMA」の意味するもの
階差数列みたいな概念「単位根過程」
説明力がありそうで説明力がない「見せかけの回帰」

順を追って解説していきます。

時系列分析でよく目にする「ARMA」の意味するもの

時系列分析というと「ARMA」というアルファベット4文字を目にしたことはないでしょうか？

この文字列は

というそれぞれの部分で成り立っており、それぞれの部分には以下のような意味があります。

MA過程とAR過程に関する解説に入る前に、それぞれの過程を考える上で重要な自己相関について説明いたします。

自己相関

自己相関とは、時系列データにおいてある元のデータと時間をずらしたデータとの相関のことを指します。

以下の図は2020年から2024年の京都の月平均気温のグラフです。

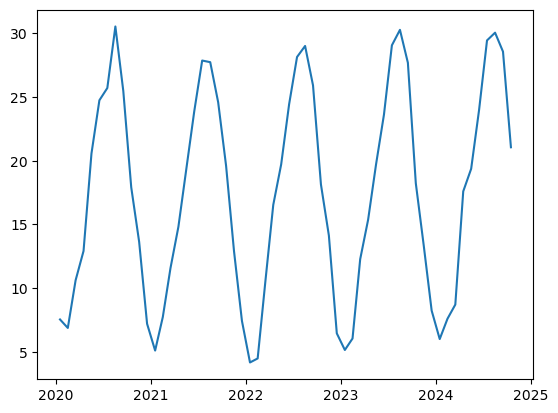
夏の時期には気温が上昇し、冬になると気温が下がるという傾向が顕著に見えており、そのような周期性が毎年繰り返されていることが分かります。

そして、以下の図は2020年から2024年までの京都の月平均気温の自己相関を取ったグラフです。

例えば、元データと2ヶ月ずれのデータとの間の相関係数が0.8程度であることが下のグラフから読み取ることができます。

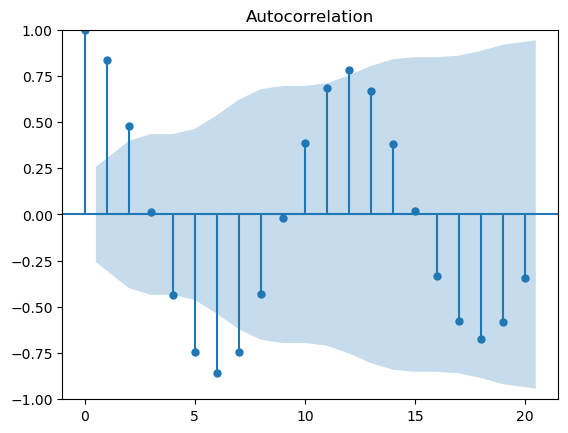
上記グラフを見ると、直近2ヶ月までが同じ傾向を示している（=自己相関係数が高い）のはもちろんですが、12ヶ月ずれ、つまり1年前の同じ月との自己相関も強いことが明らかになっており、京都における月間平均気温というデータは「12」という周期を持つことが確認できます。

自己相関の基礎知識を仕込んだところで、MA過程とAR過程の説明に入っていきましょう。

MA = 移動平均

MA（Moving Average）とは移動平均を意味し、「任意の数のホワイトノイズをパラメータ調整しながら足し合わせたもの」を意味します。

例えば、3次MA過程の式を書くと以下のようになります。

$$y_t = \mu + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \theta_3 \epsilon_{t-3} , ~~ \epsilon_{t} \sim \mathrm{W.N.}(\sigma^2)$$

ホワイトノイズとは？

時系列データにはある程度の確率的変動が存在します。

時系列データの各時点における確率的変動同士が互いに独立（=関係していない）であるなどの厳しい条件を置く場合には、その確率的変動の羅列をiid系列（independently and identically distributed = 互いに独立で同一の分布に従う）などと呼びますが、経済・ファイナンスデータにおける時系列モデルとしては少し制約が強すぎます。

例えば、リーマンショックなどの市場に対する大きな影響があった場合は、ある日の値動きと翌日の値動きはともに似たような下降傾向を示すものと考えられます。

そのため、実際の過程としてはiid系列よりも弱めの仮定としてホワイトノイズという確率的変動を使用することが多いです。

ホワイトノイズの性質は以下の3つの式で表されます。

$$E(\epsilon_t) = 0$$

$$\gamma_k = E(\epsilon_t \epsilon_{t-1}) = \sigma^2, ~~k = 0$$

$$\gamma_k = E(\epsilon_t \epsilon_{t-1}) = 0, ~~k \neq 0$$

上の3つの式は以下3つの性質を表し、iid系列よりも少し弱い仮定になっています.

全ての時点において期待値が0
全ての時点において分散が一定
異なる時点のホワイトノイズ同士は相関を持たない（=自己相関を持たない）

ホワイトノイズ$\epsilon$の期待値が0であることから、MA過程の期待値は$\mu$であると分かります。

そのため、MA過程は期待値$\mu$を中心としたランダムネスのある時系列であると考えることができます。

なお、$n$次MA過程は直近$n$個の自己相関までは表現することができますが、$n+1$個以上の自己相関は表現できないことが分かっています。

例えば、先ほどの京都の月平均気温の例では20（=グラフ右端）まで自己相関を持っていることが確認できていますが、10次MA過程で先ほどの京都の月平均気温をモデル化した場合は、高々10個までにか自己相関を表現できません。

つまり、モデル化したい元々のデータが多くの自己相関を持つ場合は、それだけMA過程のパラメータが増えてしまう、という問題があるのです。

※100次の自己相関まで表現したい場合は$\theta_1$〜$\theta_{100}$までパラメータを用意する必要があります。

続いて紹介するAR過程は、MA過程の有するパラメータの増大を回避できる可能性があるのです。

AR = 自己回帰

AR（AutoRegression）とは自己回帰を意味し、「現在の値が過去の値の式で表されること」を意味します。

例えば、現在の値が$y_t$、1つ前の値が$y_{t-1}$とすると、1次AR過程であるような式は以下のように表されます。

$$y_t = c + \phi_1 y_{t-1} + \epsilon_{t},~~\epsilon_t \sim \mathrm{W.N.}(\sigma^2)$$

※W.N. = ホワイトノイズ

MA過程においてはホワイトノイズをパラメータつきで足し合わせていましたが、AR過程では今のデータよりも前のデータをパラメータ付きで足し合わせていくこととなります。

1次AR過程における$k$個目の自己相関係数は以下のように求められることが分かっています。

$$\rho_k = \phi_1^k$$

そのため、$n$次MA過程と異なり、$n+1$個以上の自己相関係数もAR(1)過程であれば表現することが可能です。

一方で、1次AR過程における自己相関係数は$\phi_1^k$という非常に単純な形で表現されてしまうため、元データの自己相関係数が複雑であるような場合には1次AR過程ではうまく表現できないということになります。

そのため、AR過程の次数を増やして対処したり、自己回帰移動平均（ARMA）過程と呼ばれる

ホワイトノイズをパラメータ$\theta$付きで足し算する
今のデータ以前のデータをパラメータ$\phi$付きで足し算する

というMA過程とAR過程の二つの性質を組み合わせたような式で表現をすることによって、複雑な自己相関を持ったデータに対しても対処できるようにしよう、というのが本書から得たARMA過程に対する理解です。

階差数列みたいな概念「単位根過程」

MA過程が必ず持っている性質として、定常性という性質があります。

弱定常性とは？

任意の$t$と$k$に対して以下の式が成立するとき、過程は弱定常と言われます。

$$E(y_t) = \mu$$

$$Cov(y_t, y_{t-k}) = E[(y_t – \mu)(y_{t-k}- \mu)] = \gamma_k$$

つまり、以下の2つの性質が成り立つ場合に過程は弱定常であると言えます。

期待値が常に$\mu$
自己共分散が時間には依存せずに$k$によって決まる

強定常性とは？

任意の$t$と$k$に対して、$(y_t, y_{t+1}, \cdots, y_{t+k})$の同時分布が同一になる場合、過程は強定常と言われます。

つまり、弱定常性では期待値が一定で、自己共分散が時間によらないという条件であればよかったのですが、強定常性では「定常なんだから分布も同じだよね？」という非常に強い制約を持った定常性であることが分かります。

経済・ファイナンスの分野においては定常性と言えば弱定常性を扱うことが多いので、本記事においても単に定常性といった場合には弱定常性を指すものとします。

さて、弱定常性の定義に照らし合わせると期待値が必ず$\mu$であるMA過程は弱定常性を持つというのは理解しやすいと思います。

実際、MA過程の自己共分散についてもホワイトノイズの性質を使えば、時間$t$によらないことは簡単に証明することができます。

一方で、AR過程やARMA過程については必ずしも定常であるとは限らないのですが、AR特性方程式という式を活用すれば、特定のAR過程やARMA過程が定常性をもつかどうかを検証することができます。

一方で、経済・ファイナンスの世界では定常性を持たない時系列データは非常に多いです。

例えば、株価のデータはその一例で、期待値が一定などということはなく、むしろ企業の発展に伴って上昇していく傾向があります。

それでは、そのようなデータに対して先ほどまで考えたようなARMA過程のような考え方を使ってモデル化をすることは不可能なのでしょうか？

実は、定常性を持たない時系列データに対してもARMA過程のような考え方を適用することができます。

その際に必要となってくるのが、単位根過程という考え方です。

単位根過程とは？

元々の系列$y_t$が非定常過程であり、差分系列$\Delta y_t = y_t – y_{t-1}$が定常過程であるとき、過程は単位根過程と言われる

考え方としては、高校数学で習った階差数列の概念に近いです。

問題として与えられている数列が等差数列や等比数列でなかったとしても、階差数列が等差数列や等比数列であるならば、階差数列に等差数列や等比数列の公式を適用して、元々の数列を表現していく、というような考えです。

そして、単位根過程の差分系列（つまり、定常過程であるような系列）がARMA過程を適用できる条件を満たすときに、単位根過程は自己回帰和分移動平均（ARIMA）過程と呼ばれます。

本書においては、単位根過程の具体例としてランダムウォークが紹介されており、単位根過程かどうかを検定する方法なども紹介されています。

説明力がありそうでない「見せかけの回帰」

株価という予測が非常に難しく、株価を予測することを職業としている人がいたり、巷に株価を予測することを銘打った本が溢れていたりします。

ですが、本書第6章「見せかけの回帰と共和分」では、「株価を予測するのに適したデータ」が紹介されており、株価の予測をしたい人にとっては幸運この上ない展開となっています。

そのデータの性質は以下のとおりです。

そのデータはどんなに将来に渡っても入手可能なデータである
そのデータを説明変数、各国の株価データ（指標系）を目的変数として回帰分析を行なった時の係数のP値はほぼ0に近く、統計的に有意である
そのデータを説明変数、各国の株価データ（指標系）を目的変数として回帰分析を行なった時の決定係数$R^2$は最低でも0.359、高ければ0.558であり、ある程度の説明力のあるモデルとなっている

株価予測をする人にとっては夢のようなデータですね。

さて、そのデータとは一体どのようなデータなのでしょうか？

実は、そのデータとは以下の式で表されるコンピュータから人工的に生成されたランダムウォークのデータだったのです。

$$x_t = x_{t-1} + \epsilon_t, ~ \epsilon_t \sim i.i.d N(0,1)$$

そして、有用なデータだと思っていたデータはただの人工的なデータに過ぎなかったときに、人々は考えるのです。

「じゃあ、回帰分析で有意な結果が出たのはなんだったの？」と。

実は、これが「見せかけの回帰」と呼ばれるものであり、原因は説明変数も目的変数も両方とも単位根過程であったことにあります。