
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第5章「適合度検定」の演習問題2「疑似乱数の適合度検定」における疑似標準正規乱数と標準正規分布の理論値の$chi^2$適合度検定のPythonでの実装について紹介いたします!
私は今回のコード作成を通じて、正規分布や$\chi^2$分布の上側確率をPythonで求める方法について知ることができました!
皆さんも本記事を通して、統計学的側面またはPythonの実装の側面で何らかの学びを得ていただけると幸いです!
演習問題
<疑似乱数の適合度検定>
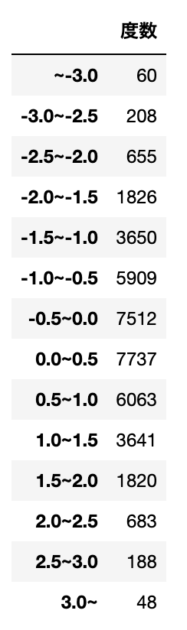
次表はある方法(ボックス・ミュラー法)によって生成した40000個の擬似標準正規乱数の度数分布である。この乱数が標準正規分布に従うという仮説の$\chi^2$適合度検定を行え(有意水準5%)
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 適合度検定 P174
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
実装コード
今回の問題を解くための実装コードは以下になります。
import numpy as np
import pandas as pd
import itertools
from scipy.stats import norm
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
#from matplotlib import rcParams
#rcParams['text.usetex'] = True
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
df = pd.read_csv('Goodness-of-fit_tests_for_pseudorandom_numbers.csv', index_col = 0)
# 生成した擬似乱数の数
N = 40000
# 標準正規分布を生成するための区間の配列を作成
base_arr = np.arange(-3,3.5, 0.5)
num_arr = [
[-3],
[ [base_arr[i], base_arr[i + 1]] for i in range(len(base_arr) - 1)],
[3]
]
num_arr =list( itertools.chain.from_iterable(num_arr))
# 確率を格納するための配列
prob_arr = []
for num_range in num_arr:
if type(num_range) == list:
# 区間の下限
lower = num_range[0]
# 区間の上限
upper = num_range[1]
# 区間の下限の上側確率
lower_prob = norm.sf(x = lower, loc = 0, scale = 1.00)
# 区間の上限の上側確率
upper_prob = norm.sf(x = upper, loc = 0, scale = 1.00)
# (区間の下限の上側確率 - 区間の上限の上側確率) = (区間の下限と上限の間の確率)
prob = lower_prob - upper_prob
else:
if num_range < 0:
# 下限値-3以下となる確率
upper_prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob = 1 - upper_prob
else:
# 上限値3以上となる確率
prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob_arr.append(prob)
df['確率'] = prob_arr
df['期待度数'] = df['確率'] * N
display(df)
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('擬似乱数は有意水準5%で適合しない')
else:
print('擬似乱数は有意水準5%で適合する')実装コード解説
実装では、以下の5ステップで問題を解いています。
- 区間の配列を作成
- 上記で作成した配列に基づいて標準正規分布の各区間の確率を生成
- 上記確率と擬似乱数の総数から期待度数を計算
- $\chi^2$値を計算
- 有意水準5%の$\chi^2$値の理論値を計算し、上記$\chi^2$値と比較する
順を追って解説していきます。
区間の配列を作成
データフレームにも「~-3.0」のような形で区間が存在しますが、標準正規分布の確率を生成する上では少し使いづらいので、まずは自力で区間の配列を作成します。
# 標準正規分布を生成するための区間の配列を作成
base_arr = np.arange(-3,3.5, 0.5)
num_arr = [
[-3],
[ [base_arr[i], base_arr[i + 1]] for i in range(len(base_arr) - 1)],
[3]
]
num_arr =list( itertools.chain.from_iterable(num_arr))まず、base_arrのところで区間を作る際の元となる配列を作成しています。
次に、num_arrの中でリスト内包表記を使って、[-3, -2.5]のような形のリストを下限の[-3]と上限の[3]以外の区間について作成しています。
最後に、リスト内包表記の箇所が[ [-3, -2.5], … , [2.5, 3]]のような形でリストが二重構造になってしまっているので、itertools.chain.from_iterableを使用することで強制的にリストを展開して、
[-3, -2.5], … , [2.5, 3]
の形式に直しています。
ここまでで標準正規分布の確率を計算するための準備は完了です。
上記で作成した配列に基づいて標準正規分布の各区間の確率を生成
先ほど作成した区間の配列を使用して、標準正規分布の確率を計算していきます。
for文を回して各区間ごとに標準正規分布から確率を計算するのですが、リストから取り出された要素が整数か配列かによって少し計算方法が異なります。
リストから取り出された要素が配列の場合
リストから取り出された要素が配列の場合というのは、[-3, -2.5]や[0, 0.5]などの区間を表す配列のことを指します。
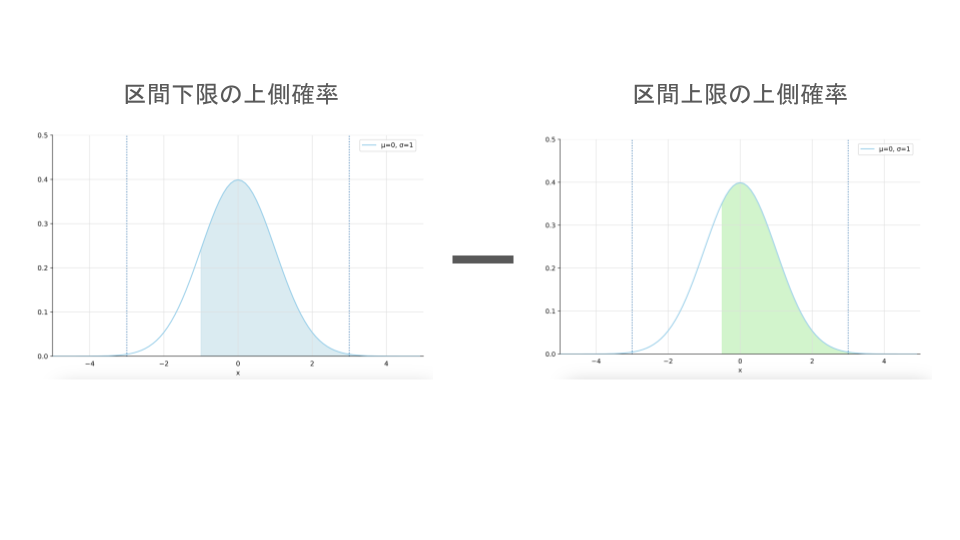
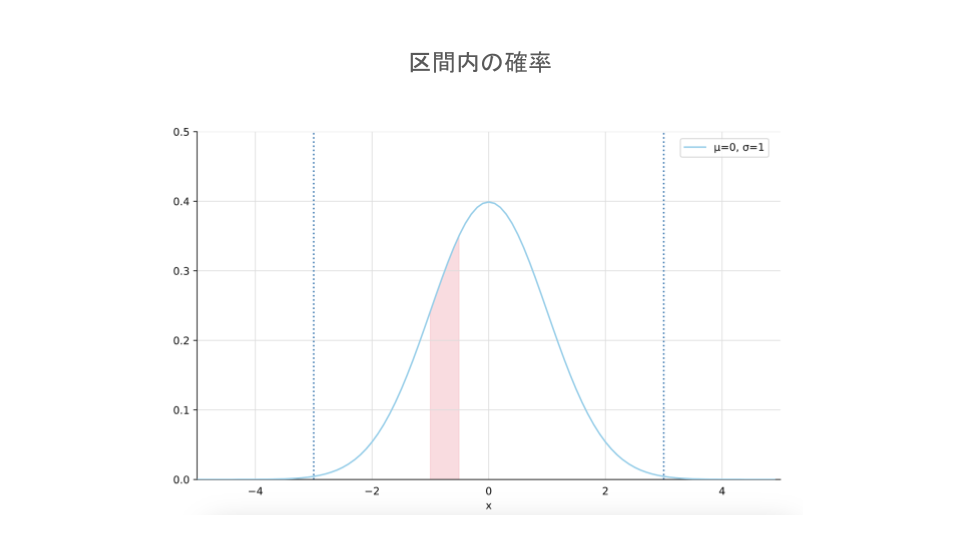
区間内の確率を計算する場合は、$(区間の下限の上側確率) – (区間の上限の上側確率)$を行うことによって、区間内の確率を求めます。
if type(num_range) == list:
# 区間の下限
lower = num_range[0]
# 区間の上限
upper = num_range[1]
# 区間の下限の上側確率
lower_prob = norm.sf(x = lower, loc = 0, scale = 1.00)
# 区間の上限の上側確率
upper_prob = norm.sf(x = upper, loc = 0, scale = 1.00)
# (区間の下限の上側確率 - 区間の上限の上側確率) = (区間の下限と上限の間の確率)
prob = lower_prob - upper_probリストから取り出された要素が整数の場合
リストから取り出された要素が整数の場合というのは、区間下限の-3の時か、区間上限の3の時です。
else:
if num_range < 0:
# 下限値-3以下となる確率
upper_prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob = 1 - upper_prob
else:
# 上限値3以上となる確率
prob = norm.sf(x = num_range, loc = 0, scale = 1.00)これらの要素の時は、それぞれ-3以下の標準正規分布の確率と3以上の標準正規分布の確率を全て求めていきます。
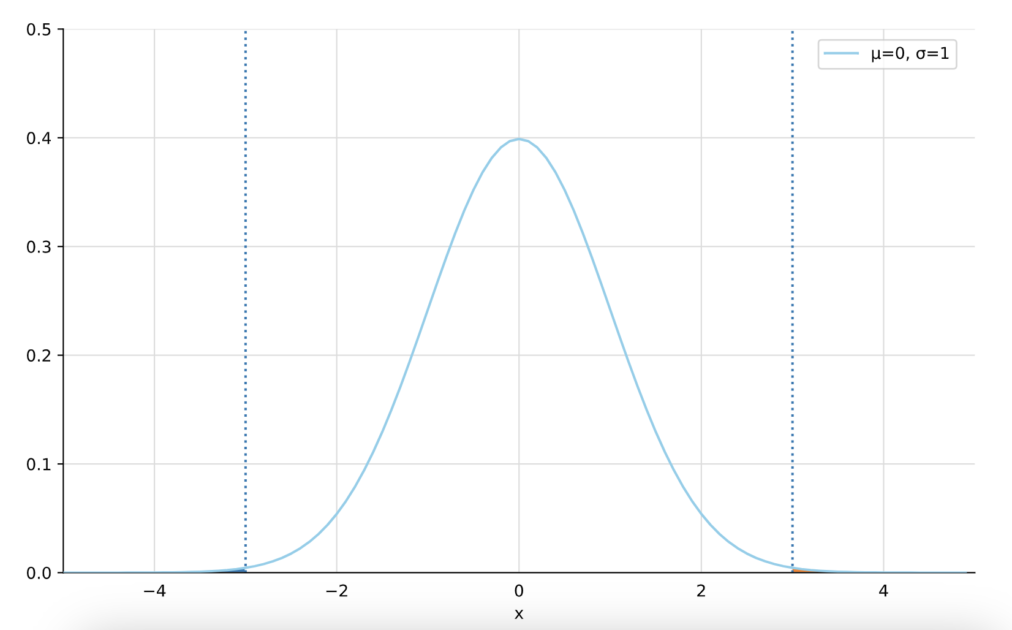
グラフの点線の部分が$x = -3$と$x = 3$なので、点線とグラフに囲まれたわずかな領域の部分の確率を求めていることになります。
上記確率と擬似乱数の総数から期待度数を計算
上記過程で、それぞれの区間における標準正規分布の確率の計算が終了しているので、
擬似乱数の数$\times$確率を計算して、期待度数を求めます。
df['確率'] = prob_arr
df['期待度数'] = df['確率'] * N
display(df)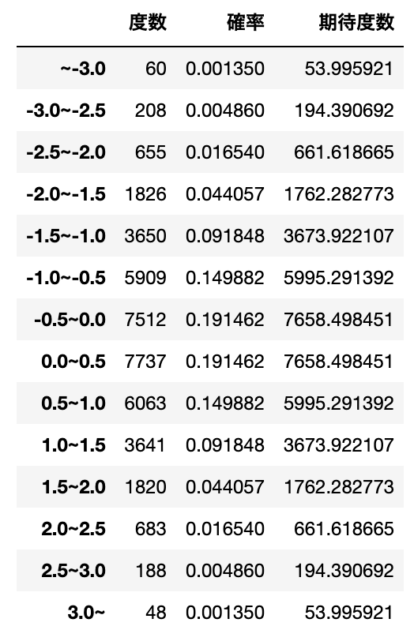
$\chi^2$値を計算
擬似標準正規乱数の度数と先ほど計算した期待度を使って、$\chi^2$値を計算します。
$\chi^2$値の計算式は以下の通りです。
ここで、$n$というのは区間の数を表し、今回でいえば「~-3.0」から「3.0~」までの14個を指します。
$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()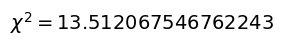
有意水準5%の$\chi^2$値の理論値を計算し、上記$\chi^2$値と比較する
今回のデータにおける$\chi^2$値の計算は終了したので、続いて$\chi^2$分布における有意水準5%の時の値を計算しましょう。
$\chi^2$値の自由度は以下のような式で求めることができます。
$$ 自由度\nu = (度数の数-1) – (あてはめたモデルの母数の個数)$$
なお、ここでいう「当てはめたモデルの母数の個数」というのは、「このデータはこのモデルに合うだろうな〜」という確率分布の積(多項分布)から最尤推定量を求めた時の母数の数のことを指しています。
要は、色々ガチャガチャと計算した時に導出される母数(分布を表すための大事なパラメータ、平均や標準偏差など)のことを指すわけです。
今回モデルとして当てはめた標準正規分布はガチャガチャと最尤推定量を求めるための計算などせず、標準正規分布の元々のパラメータ(平均0、標準偏差1)を使用しているので、「当てはめたモデルの母数の個数」は0になります。
よって、今回の$\chi^2$値を求める時の自由度$\nu$は度数の数が 14個なので、
$$ 自由度\nu = 14 -1 = 13$$
となります。
よって、scipyライブラリのscipy.stats.chi2のppfメソッドを使用して自由度13、有意水準5%の時の$\chi^2$値を調べると$\chi^2=$約22.36とわかり、
$擬似標準正規乱数における\chi^2 < \chi^2_{0.05}(13) = 22.36$であることが示されました。
これによって、擬似標準正規乱数と標準正規分布の期待度数には有意水準5%で統計的に有意な差はない、つまり大きくかけ離れてはいないのでモデルとしてはよく適合しているということが示せました。

まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第5章「適合度検定」の演習問題2「疑似乱数の適合度検定」における疑似標準正規乱数と標準正規分布の理論値の$chi^2$適合度検定のPythonでの実装について紹介しました!
データに対して何らかのモデルを当てはめてみることは、新たなデータや区間に対して外挿する際に重要ですが、「そのモデルはちゃんと適合しているのか」を調べることも同じくらい、それ以上に重要ですので、ぜひ今回紹介した適合度検定を必要に応じて実施してみてください!




コメント