
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題5「中心極限定理の実験的検証」をPythonで実装していきたいと思います。
乗算型合同法(またはM系列)による一様乱数の生成、一様乱数からの標準正規乱数の生成、正規分布の適合度検定など、自然科学の統計学で学習した内容の総まとめ的な演習問題となっているので、ぜひ問題としてチャレンジしていただけると幸いです!
問題文
<中心極限定理の実験的検証>
演習問題11.2または11.3で作成した一様乱数発生プログラムを使い、(11.10)により$X$を1,000個発生させよ
これが標準正規分布からのランダムサンプルとみなせるかどうか検定せよ
※(11.10)
$$X = \frac{U_1 + U_2 + \cdots + U_n – (n/2)}{\sqrt{n/12}}$$
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第11章 P332
演習問題11.2と演習問題11.3については以下記事にて解説をしています
実装コード
本問題を解くための実装コードは以下です。
import math
import numpy as np
import pandas as pd
import itertools
from scipy.stats import norm
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
#from matplotlib import rcParams
#rcParams['text.usetex'] = True
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
# 乗数
a = 7 ** 5
# 最大値
M = 2 ** 31 - 1
# サンプルサイズ
sample_size = 10000
# 標準正規分布のサンプルサイズ
n_sample = 1000
# 標準正規分布を作成する際の一様分布の抽出数
N = int(sample_size / n_sample)
# 適合度検定を行う際のbinの幅
bin_ = 0.5
Xs = []
XMs = []
for n in range(sample_size):
if n != 0:
Xn1 = Xs[n-1]
# X_0 = 1
else:
Xn1 = 1
X = a * Xn1
# mod
X %= M
XM = X/M
Xs.append(X)
XMs.append(XM)
## 標準正規分布の標本の作成
n_XMs = np.array([])
XMs = np.array(XMs)
for i in range(n_sample):
n_XM = (XMs[i * N : (i + 1) * N].sum() - (N / 2))/ math.sqrt(N / 12)
n_XMs = np.append(n_XMs, n_XM)
range_arr = np.arange(-3.5, 3.5, bin_)
print(f'range_arr: {range_arr}')
df = pd.DataFrame(columns = ['p', '度数', '期待度数'])
df['p'] = range_arr
for i, f in enumerate(range_arr):
print(f)
if np.abs(3.5 + f) < 0.01:
count = np.sum(n_XMs < f)
df.at[i, '度数'] = count
df.at[i, 'p'] = f'~ -3.5'
elif np.abs(3.5 - f) < 0.01:
count = np.sum(n_XMs > f)
df.at[i, '度数'] = count
df.at[i, 'p'] = f'3.5 ~ '
else:
count = np.sum((f <= n_XMs) & (n_XMs < f + bin_))
df.at[i, '度数'] = count
df.at[i, 'p'] = f'{str(round(f,3))} ~ {str(round(f + bin_, 3))}'
display(df)
# 標準正規分布を生成するための区間の配列を作成
base_arr = np.arange(-3,3.5, 0.5)
N = 1000
num_arr = [
[-3],
[ [base_arr[i], base_arr[i + 1]] for i in range(len(base_arr) - 1)],
[3]
]
num_arr =list( itertools.chain.from_iterable(num_arr))
# 確率を格納するための配列
prob_arr = []
for num_range in num_arr:
if type(num_range) == list:
# 区間の下限
lower = num_range[0]
# 区間の上限
upper = num_range[1]
# 区間の下限の上側確率
lower_prob = norm.sf(x = lower, loc = 0, scale = 1.00)
# 区間の上限の上側確率
upper_prob = norm.sf(x = upper, loc = 0, scale = 1.00)
# (区間の下限の上側確率 - 区間の上限の上側確率) = (区間の下限と上限の間の確率)
prob = lower_prob - upper_prob
else:
if num_range < 0:
# 下限値-3以下となる確率
upper_prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob = 1 - upper_prob
else:
# 上限値3以上となる確率
prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob_arr.append(prob)
df['確率'] = prob_arr
df['期待度数'] = df['確率'] * N
# カイ二乗値を計算する関数
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
display(df)
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
# 自由度と有意水準からカイ分布の値を計算
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('生成された乱数が標準正規分布に従うという仮定は有意水準5%で適合しない')
else:
print('生成された乱数が標準正規分布に従うという仮定は有意水準5%で適合する')
print()
print()解説
上記コードは以下4ステップによって解かれています。
- 乗算型合同法によって一様乱数を生成する
- 一様乱数から標準正規分布に従う乱数を生成する
- 生成した乱数から度数を作成する
- 標準正規分布の期待度数を算出する
- 度数と期待度数から$\chi^2$値を算出し、適合度検定する
順を追って解説していきます
乗算型合同法によって乱数を生成する
import math
import numpy as np
import pandas as pd
import itertools
from scipy.stats import norm
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
#from matplotlib import rcParams
#rcParams['text.usetex'] = True
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
# 乗数
a = 7 ** 5
# 最大値
M = 2 ** 31 - 1
# サンプルサイズ
sample_size = 10000
# 標準正規分布のサンプルサイズ
n_sample = 1000
# 標準正規分布を作成する際の一様分布の抽出数
N = int(sample_size / n_sample)
# 適合度検定を行う際のbinの幅
bin_ = 0.5
Xs = []
XMs = []
for n in range(sample_size):
if n != 0:
Xn1 = Xs[n-1]
# X_0 = 1
else:
Xn1 = 1
X = a * Xn1
# mod
X %= M
XM = X/M
Xs.append(X)
XMs.append(XM)乗算型合同法によって、[0,1)区間の一様乱数列XMsを作成しています。
乗算型合同法による一様乱数生成コードの解説については以下記事を参考にしていただけると幸いです。
一様乱数から標準正規分布に従う乱数を生成する
## 標準正規分布の標本の作成
n_XMs = np.array([])
XMs = np.array(XMs)
for i in range(n_sample):
n_XM = (XMs[i * N : (i + 1) * N].sum() - (N / 2))/ math.sqrt(N / 12)
n_XMs = np.append(n_XMs, n_XM)一様乱数から標準正規分布に従う乱数を生成する式
$$X = \frac{U_1 + U_2 + \cdots + U_n – (n/2)}{\sqrt{n/12}}$$
を利用して乱数を生成しています
生成した乱数から度数を作成する
range_arr = np.arange(-3.5, 3.5, bin_)
print(f'range_arr: {range_arr}')
df = pd.DataFrame(columns = ['p', '度数', '期待度数'])
df['p'] = range_arr
for i, f in enumerate(range_arr):
print(f)
if np.abs(3.5 + f) < 0.01:
count = np.sum(n_XMs < f)
df.at[i, '度数'] = count
df.at[i, 'p'] = f'~ -3.5'
elif np.abs(3.5 - f) < 0.01:
count = np.sum(n_XMs > f)
df.at[i, '度数'] = count
df.at[i, 'p'] = f'3.5 ~ '
else:
count = np.sum((f <= n_XMs) & (n_XMs < f + bin_))
df.at[i, '度数'] = count
df.at[i, 'p'] = f'{str(round(f,3))} ~ {str(round(f + bin_, 3))}'生成した標準正規分布に従う乱数から度数を作成しています。
なお、度数の区間としては、$-3.5$未満の区間と3.5より大きい区間についてはひとまとめにして計算しています。
標準正規分布の期待度数を算出する
# 標準正規分布を生成するための区間の配列を作成
base_arr = np.arange(-3,3.5, 0.5)
N = 1000
num_arr = [
[-3],
[ [base_arr[i], base_arr[i + 1]] for i in range(len(base_arr) - 1)],
[3]
]
num_arr =list( itertools.chain.from_iterable(num_arr))
# 確率を格納するための配列
prob_arr = []
for num_range in num_arr:
if type(num_range) == list:
# 区間の下限
lower = num_range[0]
# 区間の上限
upper = num_range[1]
# 区間の下限の上側確率
lower_prob = norm.sf(x = lower, loc = 0, scale = 1.00)
# 区間の上限の上側確率
upper_prob = norm.sf(x = upper, loc = 0, scale = 1.00)
# (区間の下限の上側確率 - 区間の上限の上側確率) = (区間の下限と上限の間の確率)
prob = lower_prob - upper_prob
else:
if num_range < 0:
# 下限値-3以下となる確率
upper_prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob = 1 - upper_prob
else:
# 上限値3以上となる確率
prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob_arr.append(prob)
df['確率'] = prob_arr
df['期待度数'] = df['確率'] * N次に、標準正規分布における確率と、その確率にサンプル全数をかけ算した期待度数を算出します。
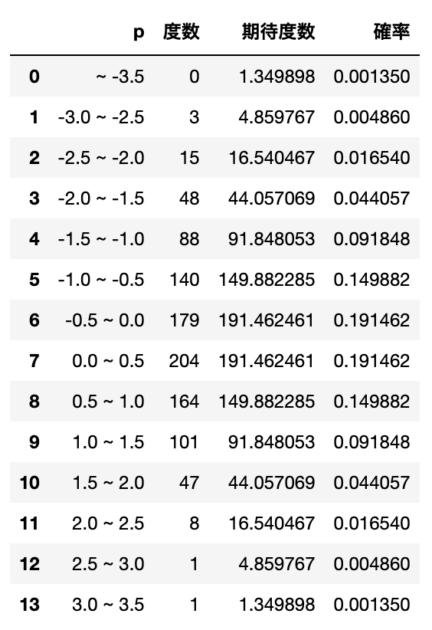
標準正規分布に関する適合度検定については以下記事を参考にしていただけると幸いです。
度数と期待度数から$\chi^2$値を算出し、適合度検定する
# カイ二乗値を計算する関数
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
display(df)
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
# 自由度と有意水準からカイ分布の値を計算
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('生成された乱数が標準正規分布に従うという仮定は有意水準5%で適合しない')
else:
print('生成された乱数が標準正規分布に従うという仮定は有意水準5%で適合する')
print()
print()最後に、ここまでで算出された度数と期待度数から$\chi^2$値を算出し、有意水準5%で適合度検定を行います。
なお、$\chi^2$値は以下の式で計算されます。
$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$
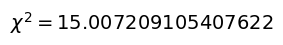

適合度検定に結果より、生成された乱数は標準正規分布に従うという仮定が適合することがわかりました。
M系列に基づく標準正規分布のランダムサンプリング
先ほどの例では乗算型合同法によって標準正規分布のランダムサンプリングを行いましたが、以下コードではM系列に基づく一様乱数から標準正規分布のランダムサンプリングを行っています
import math
import numpy as np
import pandas as pd
import itertools
import random
from scipy.stats import norm
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
#from matplotlib import rcParams
#rcParams['text.usetex'] = True
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
# 設定値
p = 127
q = 63
digits = 2 ** 3
N_uniform = 10000
bin_ = 0.1
# サンプルサイズ
sample_size = 10000
# 標準正規分布のサンプルサイズ
n_sample = 1000
# 標準正規分布を作成する際の一様分布の抽出数
N = int(sample_size / n_sample)
# 適合度検定を行う際のbinの幅
bin_ = 0.5
ans = random.choices([0,1], k = p)
for n in range(p, p * digits):
an = ans[n - p] + ans[n - q]
if an == 2:
an = 0
ans.append(an)
def bitwise_addition_no_carry(bin1, bin2):
# 長さを合わせるためにゼロ埋めする
max_len = max(len(bin1), len(bin2))
bin1 = bin1.zfill(max_len)
bin2 = bin2.zfill(max_len)
# 結果を保存するためのリスト
result = []
# 各ビットごとにXORを計算する
for b1, b2 in zip(bin1, bin2):
sum_bit = int(b1) ^ int(b2) # XORを計算
result.append(str(sum_bit))
# 結果のリストを文字列に変換する
return ''.join(result)
Xns_binary = []
Xns_decimal = []
pns = []
for i in range(p):
Xn = ans[i * digits: (i + 1) * digits]
Xn = ''.join(map(str, Xn))
Xns_binary.append(Xn)
Xn_decimal = int(Xn, 2)
pn = Xn_decimal / (2**8)
pns.append(pn)
Xns_decimal.append(Xn_decimal)
for i in range(p, N_uniform):
Xn =bitwise_addition_no_carry(Xns_binary[i - p], Xns_binary[i - q])
Xns_binary.append(Xn)
Xn_decimal = int(Xn, 2)
pn = Xn_decimal / (2 ** 8)
pns.append(pn)
Xns_decimal.append(Xn_decimal)
## 標準正規分布の標本の作成
n_XMs = np.array([])
XMs = np.array(pns)
for i in range(n_sample):
n_XM = (XMs[i * N : (i + 1) * N].sum() - (N / 2))/ math.sqrt(N / 12)
n_XMs = np.append(n_XMs, n_XM)
range_arr = np.arange(-3.5, 3.5, bin_)
print(f'range_arr: {range_arr}')
df = pd.DataFrame(columns = ['p', '度数', '期待度数'])
df['p'] = range_arr
for i, f in enumerate(range_arr):
print(f)
if np.abs(3.5 + f) < 0.01:
count = np.sum(n_XMs < f)
df.at[i, '度数'] = count
df.at[i, 'p'] = f'~ -3.5'
elif np.abs(3.5 - f) < 0.01:
count = np.sum(n_XMs > f)
df.at[i, '度数'] = count
df.at[i, 'p'] = f'3.5 ~ '
else:
count = np.sum((f <= n_XMs) & (n_XMs < f + bin_))
df.at[i, '度数'] = count
df.at[i, 'p'] = f'{str(round(f,3))} ~ {str(round(f + bin_, 3))}'
display(df)
# 標準正規分布を生成するための区間の配列を作成
base_arr = np.arange(-3,3.5, 0.5)
N = 1000
num_arr = [
[-3],
[ [base_arr[i], base_arr[i + 1]] for i in range(len(base_arr) - 1)],
[3]
]
num_arr =list( itertools.chain.from_iterable(num_arr))
# 確率を格納するための配列
prob_arr = []
for num_range in num_arr:
if type(num_range) == list:
# 区間の下限
lower = num_range[0]
# 区間の上限
upper = num_range[1]
# 区間の下限の上側確率
lower_prob = norm.sf(x = lower, loc = 0, scale = 1.00)
# 区間の上限の上側確率
upper_prob = norm.sf(x = upper, loc = 0, scale = 1.00)
# (区間の下限の上側確率 - 区間の上限の上側確率) = (区間の下限と上限の間の確率)
prob = lower_prob - upper_prob
else:
if num_range < 0:
# 下限値-3以下となる確率
upper_prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob = 1 - upper_prob
else:
# 上限値3以上となる確率
prob = norm.sf(x = num_range, loc = 0, scale = 1.00)
prob_arr.append(prob)
df['確率'] = prob_arr
df['期待度数'] = df['確率'] * N
# カイ二乗値を計算する関数
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
display(df)
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
# 自由度と有意水準からカイ分布の値を計算
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('生成された乱数が標準正規分布に従うという仮定は有意水準5%で適合しない')
else:
print('生成された乱数が標準正規分布に従うという仮定は有意水準5%で適合する')
print()
print()
M系列によって生成した標準正規分布に従う乱数の方が、乗算型合同法によって生成された標準正規分布に従う乱数よりも期待度数との差が小さいことが
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題5「中心極限定理の実験的検証」をPythonで実装していき、それぞれのコードでどのようなことを実行しているのかを解説させていただいました。
今回の記事が皆さんの独学のお役に立てれば幸いです!






コメント