
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題2「乗算型合同法による一様乱数発生プログラムの作成」をPythonで実装していきたいと思います。
乗算型合同法を知らない方にもわかるように解説させていただきますので、ご参考にしていただけると幸いです.
問題文
<乗算型合同法による一様乱数発生プログラムの作成>
適当なプログラム言語を使って、例11.2で示したパラメータを用いる乗算型合同法による乱数発生のプログラムを作成せよ。
これを用いて発生させた乱数列が表11.2のようになることを確かめよ
※例11.2において、$a, M$は以下のように設定される.
$$a = 16807(= 7^5),~M = 2^{31} – 1$$
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第11章 P331
乗算型合同法とは?
乗算型合同法とは、適当な$a, M$に対して、
$$X_n = aX_{n-1}~~(mod~M),~ n \geqq 1$$
を順次適用することによって、乱数列を得る方法です。
上式を日本語で表現すると、「$aX_{n-1}$を$M$で割った余りを$X_n$とする」ということを意味します。
乗算型合同法は線形合同法
$$X_n = aX_{n-1}+c~~(mod~M),~ n \geqq 1$$
の$c=0$のバージョンになります.
実装コード
$a = 16807, M = 2^{31} -1$であるような乗算型合同法は以下のようにPythonで実装されます。
import math
import numpy as np
import pandas as pd
# 乗数
a = 7 ** 5
# 最大値
M = 2 ** 31 - 1
# サンプルサイズ
sample_size = 30
Xs = []
XMs = []
for n in range(sample_size):
if n != 0:
Xn1 = Xs[n-1]
# X_0 = 1
else:
Xn1 = 1
X = a * Xn1
# mod
X %= M
XM = X/M
Xs.append(X)
XMs.append(XM)
df = pd.DataFrame()
df['X_i'] = Xs
df['X_i/M'] = XMs
display(df)解説
上の乗算型合同法のコードは以下のような2ステップで擬似乱数を生成しています
- パラメータ$a, M$を設定する
- $X_0 = 1$からスタートして、順次$mod~M$を計算する
順を追って解説いたします。
パラメータ$a, M$を設定する
# 乗数
a = 7 ** 5
# 最大値
M = 2 ** 31 - 1
# サンプルサイズ
sample_size = 30
Xs = []
XMs = []$X_0 = 1$からスタートして、順次$mod~M$を計算する
Xs = []
XMs = []
for n in range(sample_size):
if n != 0:
Xn1 = Xs[n-1]
# X_0 = 1
else:
Xn1 = 1
X = a * Xn1
# mod
X %= M
XM = X/M
Xs.append(X)
XMs.append(XM)上記コードでは、range(sample_size)で作成される配列の最初の数字は0であることに注意し、$n=0$である時には$X_{n-1}$を参照せずに、$X_0=1$を代入するようにしています。
上記コードでついでに計算されている$X_i / M$は区間$[0,1)$で連続な一様分布から抽出された確率変数の近似値になります。
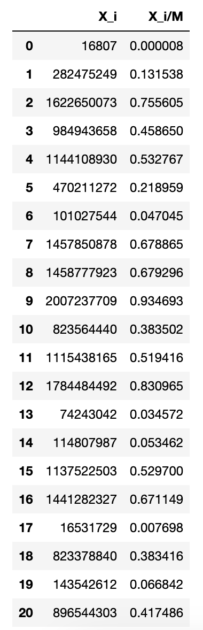
上記コードの出力結果は以下のとおりです。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題2「乗算型合同法による一様乱数発生プログラムの作成」をPythonで実装して簡単な解説をさせていただきました。
アルゴリズム自体がかなりシンプルですので、解説文は非常に短く、どちらかというとコードからアルゴリズムの挙動を読み取っていただくような記事になっていたかと思います。
上記コードをご参考いただいた皆さんはぜひ線形合同法のアルゴリズムを作成してみてください!



コメント