
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第6章-演習問題3「母平均についての2標本問題: 証明」についてスモールステップで証明をしていこうと思います。
本書だけでなく「統計学入門」からも必要なTipsを引っ張って補足いたしますので、当該問題の模範解答の証明がわかりづらかった方は参考にしていただけると幸いです!
問題文
<母平均についての2標本問題: 証明>
正規分布の母平均に関する2標本問題において、(6.15)の検定の検出方法(6.16)で与えられることを示せ。
(6.15) $$Z = \sqrt{\frac{mn}{m + n}}\cdot\frac{\bar{X} – \bar{Y}}{\sigma_0}$$
(6.16)
$$\beta_{\sigma}(\mu_1, \mu_2) = 1 – \Phi(z_{\alpha} – \tau)$$
$$\beta_{\sigma}(\mu_1, \mu_2) = 1 – \Phi(z_{\alpha/2} – \tau) + \Phi( – z_{\alpha/2} – \tau)$$
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第6章 演習問題 P199
前提知識
証明に入る前に、本問題を解くために必要な知識を2つほど仕入れておきましょう。
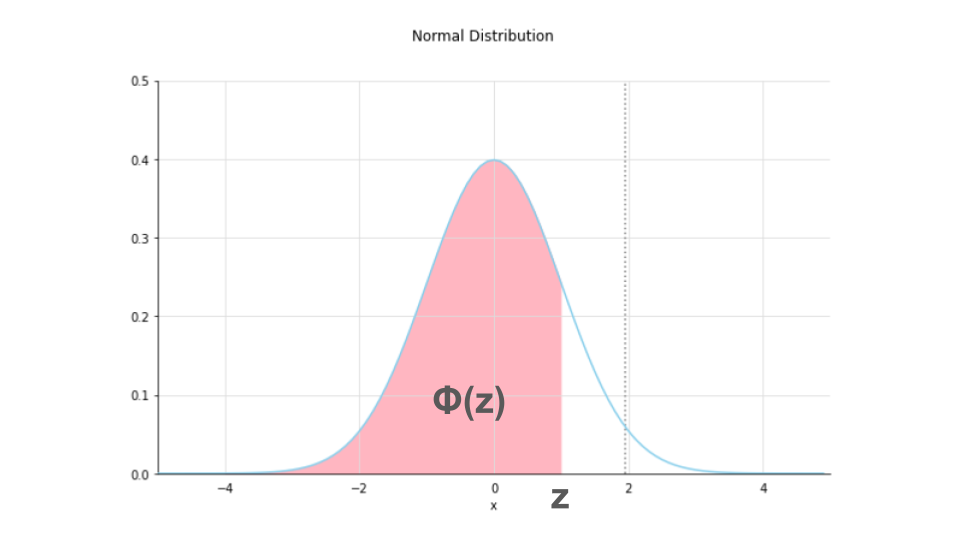
$\Phi(z)$の表すもの
問題文に登場する$\Phi(z)$は標準正規分布における点$z$までの累積分布を表します。
分散が等しい正規分布の標本平均の差の標本分布
今回の演習問題の前提となる2つの正規分布は以下のような仮定をおいています。
$X_1, \cdots, X_m$を$N(\mu_1, \sigma^2)$に従う互いに互いに独立な確率変数とし、$Y_1, \cdots, Y_n$を$N(\mu_2, \sigma^2)$に従う互いに独立な確率変数とする。
ここで、$\sigma^2 = \sigma_0^2$は既知で、また2つの母集団に共通であるとする。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第6章 P188
つまり、今回の問題において分散が等しい2つの正規分布の標本平均の差について考えることになりますが、分散が等しい2つの正規分布の標本平均を標準化した式は
$$ Z = \frac{(\bar{X} – \bar{Y}) – (\mu_1 – \mu_2)}{\sqrt{\left(\frac1m + \frac1n\right)\sigma^2}}$$
と表され、$Z$の分布は標準正規分布$N(0,1)$です。
有意水準$\alpha$の検定
有意水準が$\alpha$であるとき、検定統計量$Z$に対する片側検定・両側検定の式は以下で表されます。
- 片側検定: $Z > z_{\alpha}$
- 両側検定: $|Z| > z_{\alpha/2}$
証明
上記前提知識を利用して、今回の問題を証明していきましょう。
証明
$$\beta_{\sigma}(\mu_1, \mu_2) = P_{\mu_1, \mu_2}(Z > z_{\alpha}) = 1 – P_{\mu_1, \mu_2}\left(\sqrt{\frac{mn}{m + n}}\frac{\bar{X} – \bar{Y}}{\sigma_0}> z_{\alpha}\right) $$
ここで、$P_{\mu_1, \mu_2}$内の両辺から$\sqrt{\frac{mn}{m + n}}\left(\frac{\mu_1 – \mu_2}{\sigma_0}\right)$を引くと
$$1 – P_{\mu_1, \mu_2}\left(\sqrt{\frac{mn}{m + n}}\left(\frac{(\bar{X} – \bar{Y}) – (\mu_1 – \mu_2)}{\sigma_0}\right) > z_{\alpha} – \sqrt{\frac{mn}{m+n}}\frac{\mu_1 – \mu_2}{\sigma_0}\right)$$
ここで、$\sqrt{\frac{mn}{m + n}}\left(\frac{(\bar{X} – \bar{Y}) – (\mu_1 – \mu_2)}{\sigma_0}\right)$は分散が等しい正規分布の標本平均を標準化した式であり、標準正規分布に従う。
よって、標準正規分布の累積分布$\Phi(z)$を使うことができる。
分散が等しい正規分布の標本平均の標準化した式の変形
$$\frac{(\bar{X} – \bar{Y}) – (\mu_1 – \mu_2)}{\sqrt{\left(\frac1m+\frac1n\right)\sigma^2}} = \frac{(\bar{X} – \bar{Y}) – (\mu_1 – \mu_2)}{\sqrt{\frac{m+n}{mn}}\sigma} = \sqrt{\frac{mn}{m+n}}\frac{\mu_1 – \mu_2}{\sigma}$$
$\tau = \sqrt{\frac{mn}{m+n}}\frac{\mu_1 – \mu_2}{\sigma_0}$とおくと、求める$\beta_{\sigma}(\mu_1, \mu_2)$は
$$\beta_{\sigma}(\mu_1, \mu_2) = 1 – \Phi(z_{\alpha} – \tau)$$
両側検定の場合も同様にして、
$$\beta_{\sigma}(\mu_1, \mu_2) =$$
$$1 – P_{\mu_1, \mu_2}\left(-z_{\alpha/2} – \sqrt{\frac{mn}{m+n}}\frac{\mu_1 – \mu_2}{\sigma_0}
< \sqrt{\frac{mn}{m + n}}\left(\frac{(\bar{X} – \bar{Y}) – (\mu_1 – \mu_2)}{\sigma_0}\right) < z_{\alpha} – \sqrt{\frac{mn}{m+n}}\frac{\mu_1 – \mu_2}{\sigma_0}\right)$$
$$ = 1 – \Phi(z_{\alpha} – \tau) + \Phi(-z_{\alpha} – \tau)$$
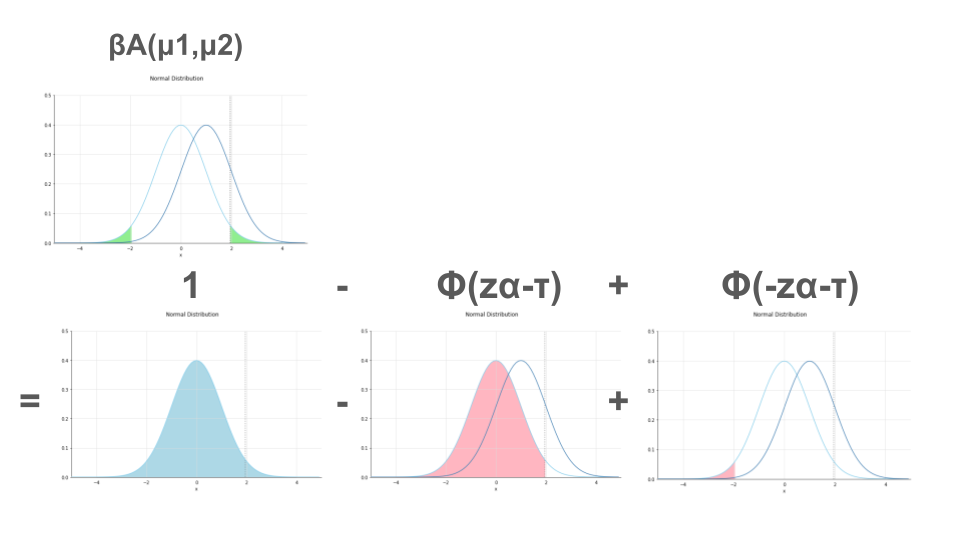
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第6章-演習問題3「母平均についての2標本問題: 証明」について、最初に証明に必要な前提知識を共有しながら解説をしていきました。
今回の問題におけるTipsとして、分散が等しい正規分布の標本平均の差の標本分布の式を覚えていただけると幸いです。



コメント