
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、以下のPython公式ドキュメントの「to_bytes」の記事に記載されている「(x.bit_length() + 7 ) // 8」が何を意味しているのか、私なりに噛み砕いて解説してみました!
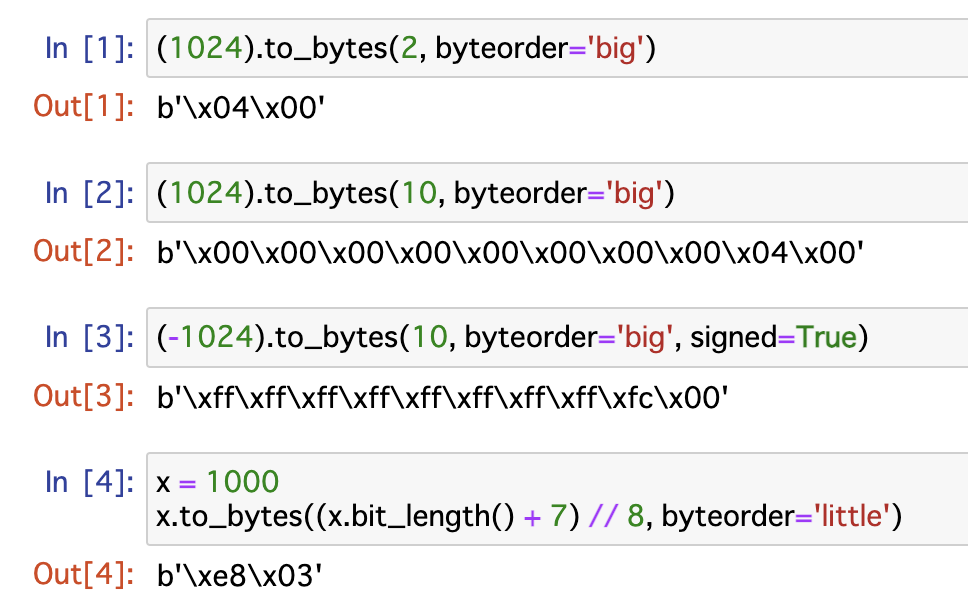
私が初見で見た時には何が書いてあるか理解できなかったので、同じように困っている人の助けになることができれば幸いです!
時間がない人のための3行要約
そもそもto_bytes()ってどんな関数?
to_bytes()関数は、ある数字を16進数のバイト列で表現してくれる関数です。
バイト列とは?
バイト列を理解するためには、そもそも「バイトってなに?」というところから理解する必要があります。
そして、バイトを理解するためには「ビット」について理解する必要があります。
そしてそして、ビットを理解するために必要なものは、「バイナリ」です。
バイナリとは大ざっぱにいうと2進数のことを表します。
そして、ビットとはバイナリ(2進数)で表すときに必要な桁数のことです。
例えば、10という数字は2進数では1010と表されるので、4ビット必要であることがわかります。
17という数字も2進数では10001と表されるので5ビット必要であることがわかります。
そして、バイトとビットの間には1バイト=8ビットという関係が成り立っています。
つまり、バイト列とは1バイトで8ビット分表すことができる情報のことを言います。
8ビット分の情報とは具体的には2進数でいうと、最大11111111、つまり10進数でいうところの255までの数字分の情報量を表すことができます。
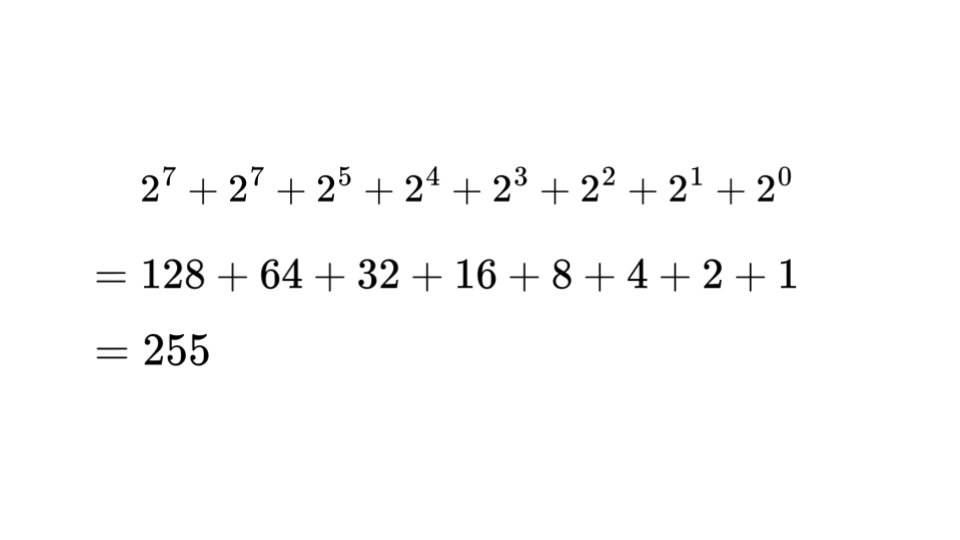
ここで、 10進数の255を16進数で表すとffと表されるので、このffまでが1バイト分の情報量に当たります。
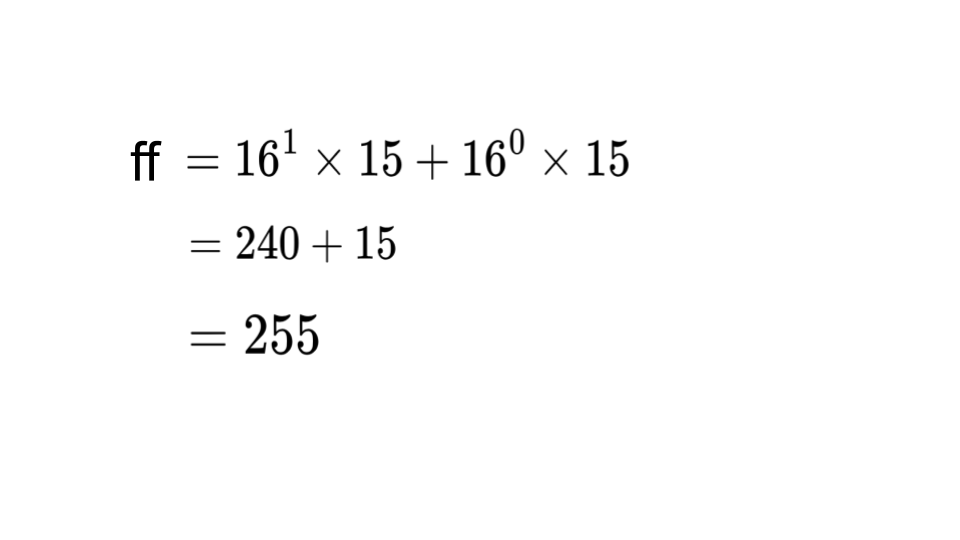
16進数とは?
16進数とは、1桁が0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,Fで表される数字の表記方法です。
2進数が0,1の2つの数字、10進数が0,1,2,3,4,5,6,7,8,9の10つの数字で表されるように、
16進数はアルファベットのA~Fを含めた16個の数字とアルファベットで表されます。
16進数を10進数に直す時にはA=10, B=11, C=12, D=13, E=14, F=15と考え、各桁の16の○乗と各桁の数字またはアルファベットを掛け算して、最終的に全ての数字を足すと10進数に直すことができます。


ここで、第1引数にはバイト列の長さを指定することができます。
この場合のバイト列とは16進数バイト列のことです。
なお16進数バイト列では、1バイトを使って10進数の0( = b”)から255(= b’\xff’)までを表すことができます。
例えば、以下のように1024という10進数の数字をto_bytes()を使って、2バイト列を返すように指定すると、1024を16進数(\xつき)で表現したb’\x04\00’が返ってきます。

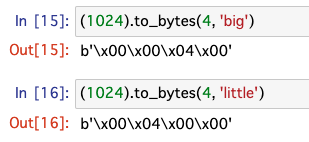
第2引数のbyteorderはbigを指定すればバイト列は左から大きい順に、littleを指定すればバイト列は左から小さい順に記載されます。
10進数で言うと、「115」という数字がbigと指定すると「115」と記述されて、littleと記述すると「511」と記述されるイメージですね。
参考リンク:組み込み型(to_bytes) / 組み込み型(bit_len
bit_length()関数とは?
bit_length()関数は、ある数字を2進数で表したときに、何ビットの2進数で表されるのかを教えてくれる関数です。
例えば、10進数の12であれば2進数では1100と表されますので、bit_length()関数は4(ビット)と返してくれるわけです。
Pythonの公式ドキュメントのto_bytesの項目を見てみる
ここまでの知識を踏まえて、今回取り上げている「Python公式ドキュメントのto_bytes」のところに記載してあるコードをもう一度見てみましょう。

ここまでの解説を踏まえれば、In[1]のコードは「1024を2バイトの16進数に変換している」と理解いただけるかと思います。
In[2]のコードについても同様に「1024を10バイトの16進数に変換している」と理解いただけるかと思います。
元々1024は2バイトの16進数で表されますので、上位8バイトにはひたすら\x00が記載してあるのが終わりいただけるかと思います。
ln[3]のsignedは初耳かと思いますが、signedはマイナスの値を表す時に使います。
16進数の世界では1024の10バイトの16進数表記、b’\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00’に対応するb’\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00’のことを補数と呼んでおり、10進数では-1024を意味します。
ある数の補数とは、ある数(1024)とある数の補数(-1024)を足して0になる数字を覚えておいてください。
実際に2つの16進数を足し算するとb’\x01\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00’となりますが、この16進数は11バイトと元々の11バイトをオーバーしてしまっているため、オーバーしているバイトは削除され、b’\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00’、つまり10進数でいう0になってしまいます。
さて、ここで問題になってくるのはIn[4]です。
byteorder=’little’は左から大きい順にバイト列を記述するルールでしたが、少しめんどくさいのでIn[5]でbyteorder=’big’に書き換えてしまいましょう。

すると、\x03\xe8は1000を16進数で表記したものであることが分かります。

そして、\x03\xe8というのは2バイトの16進数で記述されていることが分かります。
つまり、to_bytes()関数の第1引数に入っている「( x.bit_length() + 7 ) // 8 = 2」ということが分かります。
それでは、この「( x.bit_length() + 7 ) // 8」という処理は、どのようなことを行なっているのでしょうか。
ここから先は段階を追って考えていきましょう。
bit_length()とは何か?
bit_length()は整数を二進数で表すために必要なビットの数を表します。
例えば、10進数の2は2進数で11と表されるので、(2).bit_length()は2です。
10進数の4は2進数で100と表されるので、(4).bit_length()は3です。

16進数1バイトは2進数何バイト分まで表すことができるのか?
ここでbit_length() + 7 について考える前に、 16進数1バイトが2進数何バイト分まで表すことができるのかを考えてみましょう。
16進数1バイトで\x00から\xffまで表すことができます。
そして\x00は当然のことながら10進数でいう0を、\xffはf=15ですので、10進数で[mathjax]\(15 \times 16 + 15 = 255\)まで表すことができます。
ここで、2進数のことを考えてみると、1バイト=8ビットで00000000〜11111111まで表すことができます。
2進数の00000000は10進数で0、2進数の11111111は10進数で255を表します。
ここで、つまり10進数で0〜255までは2進数でも16進数でも1バイトで表すことができることがわかります。
ここで、考えなければならないのは、2進数9ビット、つまり1バイトよりも少し大きな2進数は16進数何バイトで表すことができるのでしょうか。
正解は2進数9ビットは16進数2バイトで表すことができます。
例えば、10進数でいう256は2進数では100000000(9ビット)で表されますが、16進数では\x01\x00、つまり2バイトで表されます。
同様に、2バイトより1ビット大きな2進数17ビットは、16進数3バイトで表されます。
つまり、[mathjax]\(8 \times x\)ビットより小さいビット数で表される場合は[mathjax]\(x\)バイトの16進数で表されるということです。
bit_length() + 7 は何を表しているのか?
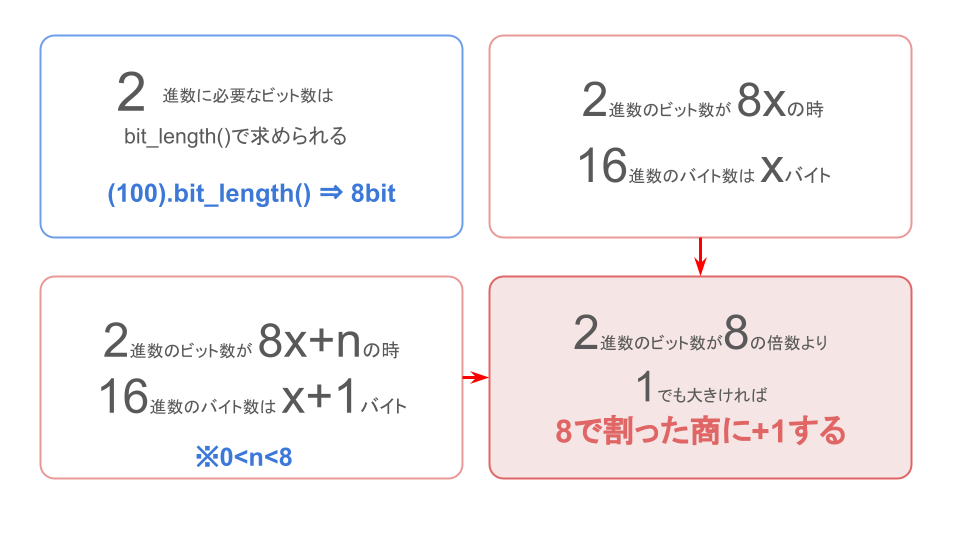
先ほどの話を整理すると、2進数のビット数と16進数のバイト数には以下のようなルールが成り立っています。
- ある10進数を2進数で表す時に必要なビット数はbit_lengthで求めることができる
- 2進数のビット数が8の倍数の時、つまり[mathjax]\(8x\)の時は、[mathjax]\(x\)バイトの16進数で表すことができる。
- 2進数のビット数が8の倍数でない時は、つまり[mathjax]\(8x + 1\)の時は、[mathjax]\(x + 1\)バイトの16進数で表すことができる。
- 2進数のビット数が8の倍数かどうかは、8で割った時に余りがあるかどうかで判断することができる
それでは、わざわざbit_lengthに7を足す意味はなんでしょうか。
その理由は、ルール3の「8の倍数でない時は[mathjax]\(x + 1\)バイトの16進数で表すことができる」という部分が少しわかりずらいことにあります。
8の倍数かどうかを判断するためには2進数のビット数を8で割る必要があり、8で割り切れなかった場合は8で割った時の商に1を足す必要があります。
実は、(x.bit_length() + 7 ) // 8 を考えた人は、この「1を足す」という動作を面倒くさがったのです。
それでは、bit_lengthに7を足すことのどのような点が良いのでしょうか。
それは、「余りを気にせずに8で割った時の商がそのまま16進数のバイト数になる」という点です。
( bit_length() + 7 ) // 8 の表すものとは?
具体的な計算をして、( bit_length() + 7 ) // 8 が16進数で表す時のバイト数を表現していることを確認していきましょう。
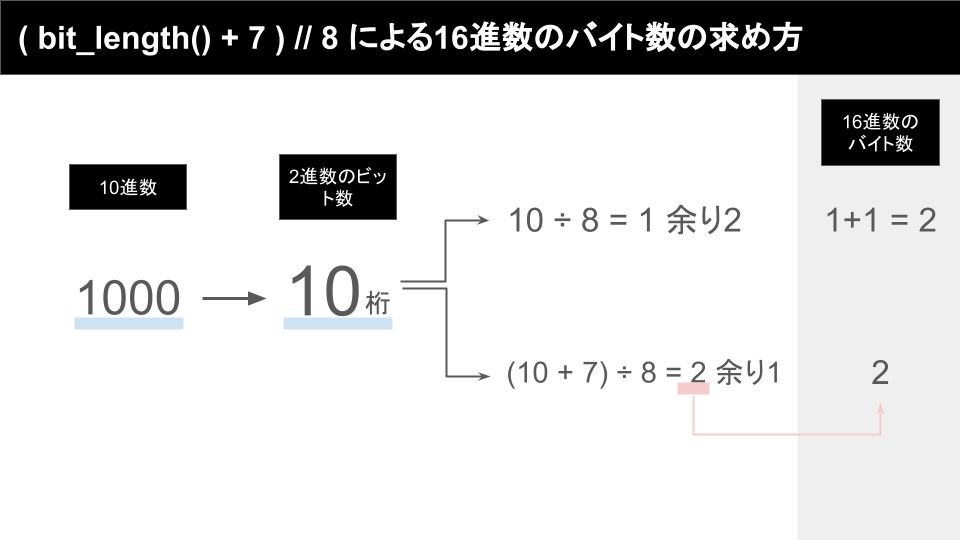
例えば、1000という数字について考えてみることにします。
bit_length()を使うと1000という数字は2進数では10ビットで表されることが分かります。
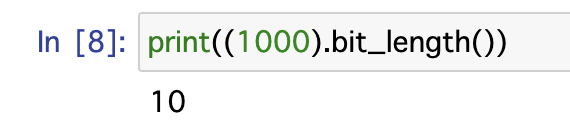
さて、10進数の1000は2進数では10ビットで表されるということは、8で割ると1余り2になるので、16進数で表す際には2バイト必要になることがわかります。
ここで、「2進数では10ビット」の10ビットに7を足すと18ビットになります。
そしてこれを8で割ると2余り1です。
つまり、7を足してから8で割った時の商2がそのまま16進数のバイト数になってくれるのです。
これが今回の( bit_length() + 7 ) // 8のカラクリです。
つまり、
「8で割った時、余りが出なかったら商がそのまま16進数のバイト数に、余りが出たら商+1が16進数のバイト数になる」
という求め方だったのが、2進数のビット数に7を足すことによって
「8で割った時の商がそのまま16進数のバイト数になる」と求め方が非常にすっきりするのです。
まとめ
本記事ではPython公式ドキュメントのto_bytesに記載のある「( x.bit_length() + 7)//8」とはどういう意味なのかについて、私なりに噛み砕いて説明してみました。
分かりにくい部分があれば随時追加の解説を入れますので、コメント欄でご指摘してください!



コメント