
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題3「両モデルの推定値比較」をPythonで実装して解いてみたので、その手順について解説いたします!
演習問題の主題としては、両モデルの推定量は前提としているモデルの違いから比が$\frac{\pi}{\sqrt{3}}$倍になるということなので、それを検証しに行く問題です!
皆さんもプロビットモデルとロジットモデルの推定量の違いを実際に推定値から実感してみてください!
問題文
<両モデルの推定値比較>
プロビット・モデルとロジット・モデルによる$\beta_1,~\beta_2$の推定値を比較して、対応する値の比が$\pi/\sqrt{3}$程度になることを、本章のいろいろなデータの分析結果から確認せよ。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第8章 演習問題 P249
プロビットモデル・ロジットモデルとは?
プロビットモデルとは、1/0のような二値$Y_i$を予測するような回帰問題において、説明変数が$X_i$であるとすると、条件付き確率
$$P(Y_i|X_i) = F^*(X_i)$$
の$F^*(X_i)$に標準正規分布を仮定する時の予測モデルのことを言います。
$$標準正規分布の累積分布関数~~~F^*(X_i) = \Phi(\beta_0 + \beta_1 X_i) = \int_{-\infty}^{\beta_0 + \beta_1 X_i} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$$
一方で、$F^*(X_i)$にロジスティック分布を仮定するとき、そのモデルをロジットモデルと呼びます。
$$ロジスティック分布の累積分布関数~~~F^*(X_i) = \Lambda(\beta_0 + \beta_1 X_i) = \frac{e^{\beta_0 + \beta_1 X_i}}{1 + e^{\beta_0 + \beta_1 X_i}}$$
この2つの関数が条件付き確率の分布の仮定に使用されている大きな理由は、累積分布関数が0~1に収まるという性質が、「確率は0%~100%に収まっていて欲しいよね」という点とマッチするからです。
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
実装コード
今回の問題を解くための実装コードは以下のとおりです。
import numpy as np
import pandas as pd
from statsmodels.formula.api import ols, logit, probit
import math
print(f'π/√3 = {math.pi / math.sqrt(3)}')
# 推定値の比を計算する関数
def calc_ratio(formula, df):
# プロビットモデルの作成
res_probit = probit(formula, data = df).fit()
print(res_probit.summary())
# ロジットモデルの作成
res_logit = logit(formula, data = df).fit()
print(res_logit.summary())
# 推定値の抽出・比の導出
for i, (pb, lb) in enumerate(zip(res_probit.params, res_logit.params)):
print(f'lb{i} / pb{i} = {lb / pb}')
# 薬物投与による死亡率のデータ
df = pd.read_csv('Log_Concentration_by_Individual_Case_Death_Survival.csv')
formula = 'Yi ~ Xi'
calc_ratio(formula, df)
# コース選択のデータ
df = pd.read_csv('Students_choice_of_two_courses_A_and_B.csv', index_col = 0)
formula = 'コース選択 ~ 性別 + 前期試験成績 + 専攻'
calc_ratio(formula, df)
# 車購入のデータ
df = pd.read_csv('market_research.csv', index_col = 0)
formula = '車購入の有無 ~ 収入 + 性別 + 居住地域'
calc_ratio(formula, df)解説
今回の問題では、以下の3ステップで推定値の比を求めています。
- $\frac{\pi}{\sqrt{3}}$の値を求める
- プロビットモデルとロジットモデルを作成し、推定値の比を求める関数を作る
- データフレームを読み込み、回帰式を作成して関数に適用する
順を追って解説していきます。
$\frac{\pi}{\sqrt{3}}$の値を求める
print(f'π/√3 = {math.pi / math.sqrt(3)}')まずは、$\frac{\pi}{\sqrt{3}}$が具体的にどのような値になるのかを算出します。
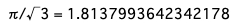
計算結果から、約1.81になることがわかりました。
プロビットモデルとロジットモデルを作成し、推定値の比を求める関数を作る
import numpy as np
import pandas as pd
from statsmodels.formula.api import ols, logit, probit
import math
# 推定値の比を計算する関数
def calc_ratio(formula, df):
# プロビットモデルの作成
res_probit = probit(formula, data = df).fit()
print(res_probit.summary())
# ロジットモデルの作成
res_logit = logit(formula, data = df).fit()
print(res_logit.summary())
# 推定値の抽出・比の導出
for i, (pb, lb) in enumerate(zip(res_probit.params, res_logit.params)):
print(f'lb{i} / pb{i} = {lb / pb}')各データに対して、繰り返しモデル作成と比の計算を繰り返すので、先に関数化しておきます。
各モデルのparamsには、推定値が配列として格納されているので、for文で順番に取り出し、推定値の比を計算していきます。
データフレームを読み込み、回帰式を作成して関数に適用する
# 薬物投与による死亡率のデータ
df = pd.read_csv('Log_Concentration_by_Individual_Case_Death_Survival.csv')
formula = 'Yi ~ Xi'
calc_ratio(formula, df)
# コース選択のデータ
df = pd.read_csv('Students_choice_of_two_courses_A_and_B.csv', index_col = 0)
formula = 'コース選択 ~ 性別 + 前期試験成績 + 専攻'
calc_ratio(formula, df)
# 車購入のデータ
df = pd.read_csv('market_research.csv', index_col = 0)
formula = '車購入の有無 ~ 収入 + 性別 + 居住地域'
calc_ratio(formula, df)本書の中にあるデータを使用して、推定値の比の算出を行っていきます。
今回のコードでは以下3つのデータを使用しました。
- 薬物濃度と生物の死亡数(P232)
- 学生のA,Bの2コースの選択(P245)
- 車の購入に関するアンケート(P250)
順に結果を見ていきましょう。
薬物濃度と生物の死亡数(P232)
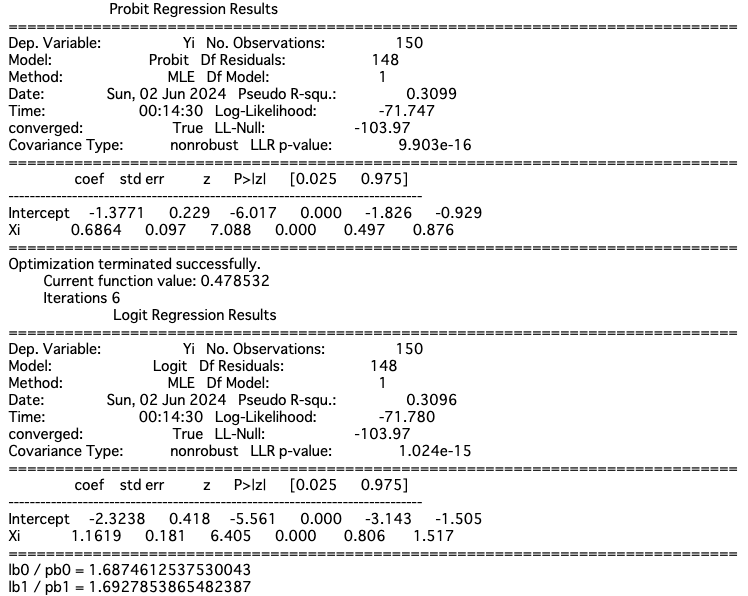
2つの推定値の比は約1.68~1.69と、1.81から遠からぬ数値が算出されています。
学生のA,Bの2コースの選択(P245)
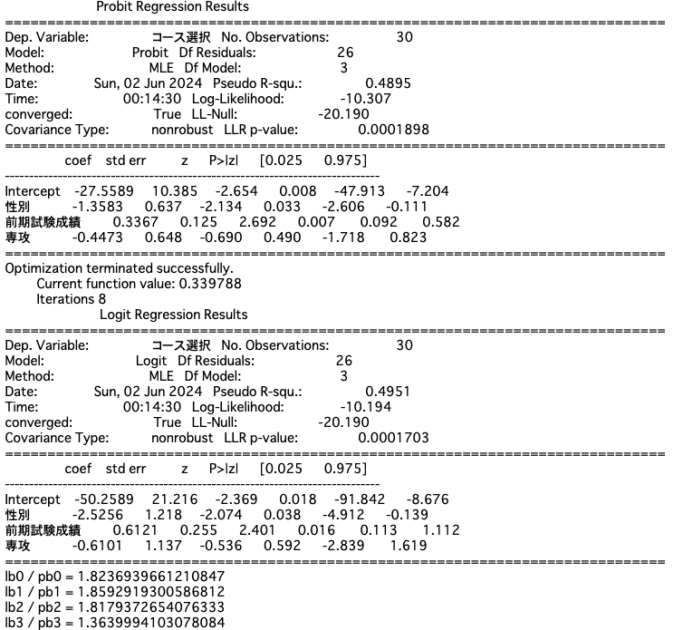
切片、性別、前期試験成績については1.81にかなり近しい比が算出されていることがわかります。
車の購入に関するアンケート(P250)
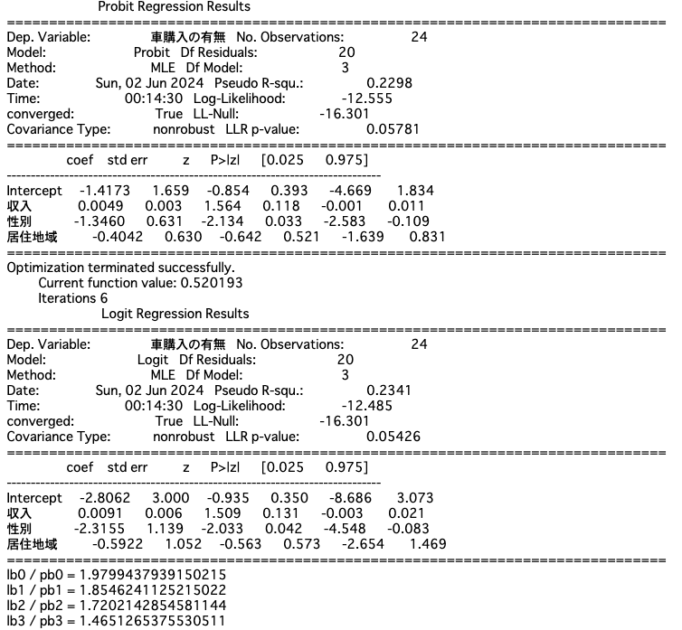
このデータについては、切片、収入、性別についてはそれなりに1.81に近しい数字になっていますが、居住地域は大きく外れた値となっています。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題3「両モデルの推定値比較」をPythonで実装して解いてみたので、その手順について解説いたしました。
結果として、コース選択のデータの推定値の比が1.81に近いという結果になりました。
3つのデータの擬似$R^2$(Pseudo R-squ)を見てみると、コース選択のデータが最も擬似$R^2$が高いので、モデルに対する当てはまりがいいほど、推定値の比が1.81に近づくのかもしれませんね。




コメント