
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題5「市場調査」におけるプロビットモデル・ロジットモデルをPythonで実装し、問題を解いてみたのでその解法について解説していきます!
本解説のプロビットモデル・ロジットモデルはformula内の目的変数・説明変数を書き換えれば、そのまま活用することができますので、ぜひご活用ください!
問題文
<市場調査>
消費者24名を対象に、車を購入したかどうかのアンケートを実施したところ、次のような結果を得た。
※車購入の有無 → 0: 購入せず, 1: 購入
※性別 → 0: 男性, 1: 女性
※居住地域 → 0: 都市に居住, 1: 農村に居住
i ) 車購入を予測するプロビット、ロジット・モデルを作り、それを推定せよ
ii ) 適当な帰無仮説(および対立仮説)を設定し検定せよ
a ) 収入は車の購入に影響するか
b ) 性別と居住地域は(同時に)車の購入に影響するか
iii ) 収入500万円の都市に居住する男性が車を購入する確率を求めよ。また、その確率の95%信頼区間を求めよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章 演習問題 P229
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
プロビットモデル・ロジットモデルとは?
プロビットモデルとは、1/0のような二値$Y_i$を予測するような回帰問題において、説明変数が$X_i$であるとすると、条件付き確率
$$P(Y_i|X_i) = F^*(X_i)$$
の$F^*(X_i)$に標準正規分布を仮定する時の予測モデルのことを言います。
$$標準正規分布の累積分布関数~~~F^*(X_i) = \Phi(\beta_0 + \beta_1 X_i) = \int_{-\infty}^{\beta_0 + \beta_1 X_i} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$$
一方で、$F^*(X_i)$にロジスティック分布を仮定するとき、そのモデルをロジットモデルと呼びます。
$$ロジスティック分布の累積分布関数~~~F^*(X_i) = \Lambda(\beta_0 + \beta_1 X_i) = \frac{e^{\beta_0 + \beta_1 X_i}}{1 + e^{\beta_0 + \beta_1 X_i}}$$
この2つの関数が条件付き確率の分布の仮定に使用されている大きな理由は、累積分布関数が0~1に収まるという性質が、「確率は0%~100%に収まっていて欲しいよね」という点とマッチするからです。
実装コード
本問題を解くコードは以下のとおりです。
なお、ブログ主の力不足で、(iii)のみ完答とはなっていないことをご了承ください.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import py4macro
import wooldridge
from py4etrics.hetero_test import *
from scipy.stats import logistic, norm, chi2
from statsmodels.formula.api import ols, logit, probit
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
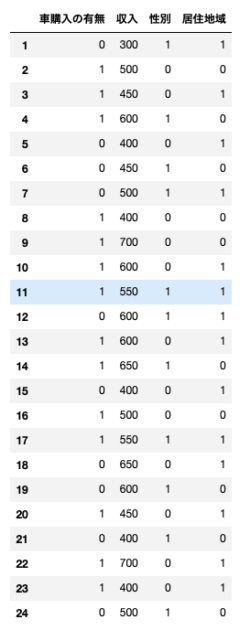
df = pd.read_csv('market_research.csv', index_col = 0)
display(df)
### (i)
# 回帰式の立式
formula = '車購入の有無 ~ 収入 + 性別 + 居住地域'
# プロビットモデルの導出
res_probit = probit(formula, data =df).fit()
print(res_probit.summary())
print()
print()
# ロジットモデルの導出
res_logit = logit(formula, data = df).fit()
print(res_logit.summary())
### (iii)
# プロビットモデルの係数を使って、回帰式を作成する
def probit_formula(income, sex, region):
y = 0.004885 * income -1.3460 * sex -0.4042 * region -1.4173
return y
# ロジットモデルの係数を使って、回帰式を作成する
def logit_formula(income, sex, region):
y = 0.009059 * income -2.3155 * sex -0.5922 * region -2.8062
return y
# 具体的な値を代入
probit = probit_formula(500, 0, 0)
# 標準正規分布の累積分布関数に代入する
pi = norm.cdf(probit)
print(f'プロビットモデルでのPi: {pi}')
### 分散を求める式が間違いの可能性あり
sigma = pi * (1 - pi)/2
print(f'プロビットモデルでの分散: {sigma}')
# 信頼区間の導出
lower = pi - 1.96 * np.sqrt(sigma)
upper = pi + 1.96 * np.sqrt(sigma)
if lower <0:
lower = 0
if upper > 1:
upper = 1
print(f'プロビットモデルによる信頼区間: [{lower}, {upper}]')
print()
# 具体的な値を代入
logit = logit_formula(500, 0, 0)
# ロジスティック分布の累積分布関数に代入する
pi = logistic.cdf(logit)
print(f'ロジットモデルでのPi: {pi}')
### 分散を求める式が間違いの可能性あり
sigma = pi * (1 - pi)/2
print(f'ロジットモデルでの分散: {sigma}')
# 信頼区間の導出
lower = pi - 1.96 * np.sqrt(sigma)
upper = pi + 1.96 * np.sqrt(sigma)
if lower <0:
lower = 0
if upper > 1:
upper = 1
print(f'ロジットモデルによる信頼区間: [{lower}, {upper}]')(i)の解説
(i)は以下2ステップによって、プロビットモデル・ロジットモデルを作成しています。
- 回帰式を作成する
- scipyライブラリやstatsmodelsライブラリを利用して、プロビットモデル・ロジットモデルによってモデルの推定を行う
順を追って解説していきます.
回帰式を作成する
df = pd.read_csv('market_research.csv', index_col = 0)
display(df)
### (i)
# 回帰式の立式
formula = '車購入の有無 ~ 収入 + 性別 + 居住地域'本問題においては、車購入の有無を目的変数とし、収入・性別・居住地域を説明変数とするため、formulaに目的変数と説明変数を書き込みます。
なお、今回のモデルにおいては交互作用は考慮しません。
scipyライブラリやstatsmodelsライブラリを利用して、プロビットモデル・ロジットモデルによってモデルの推定を行う
# プロビットモデルの導出
res_probit = probit(formula, data =df).fit()
print(res_probit.summary())
print()
print()
# ロジットモデルの導出
res_logit = logit(formula, data = df).fit()
print(res_logit.summary())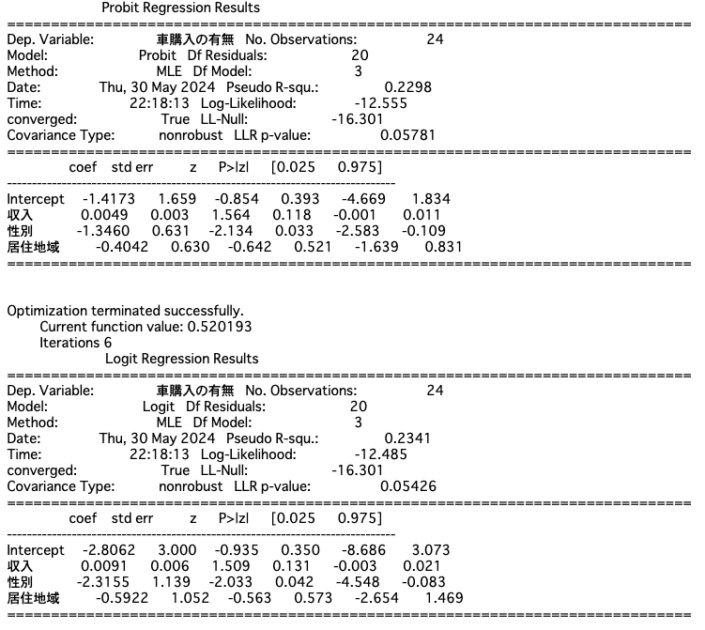
scipyライブラリとstatsmodelsライブラリを使えば、プロビットモデルもロジットモデルも最も簡単に実装することができます。
||| プロビットモデル
$$Y_i = -1.4173 + 0.0049 \times X_1 -1.3460 \times X_2 – 0.4042 \times X_3$$
||| ロジットモデル
$$Y_i = -2.8062 + 0.0091 \times X_1 -2.3155 \times X_2 – 0.5922 \times X_3$$
なお、モデルの当てはまりの良さを表す擬似$R^2$(= Pseudo R-squ)や対数尤度(=Log-Likelihood)を見ると、ロジットモデルの方が少し当てはまりがいいようです。
(ii)の解説
本書にある帰無仮説に対して、プロビットモデル・ロジットモデルの結果から検定を行っていきましょう。
収入は車の購入に影響するか
収入に関する信頼区間を見ると、プロビットモデルにおいては$[-0.001,~0.011]$、ロジットモデルにおいては$[-0.003,~0.021]$と、「影響がない」ことを意味する0を信頼区間の中に含んでいます。
よって、帰無仮説「収入は車の購入に影響しない」は有意水準5%で棄却されないこととなります。


性別と居住地域は(同時に)車の購入に影響するか
性別と居住地域の両方が同時に車の購入に影響しないという帰無仮説の検定は、2つの説明変数を含まないモデルの対数尤度$L_0$と、2つの説明変数を含むモデルの対数尤度$L_1$から以下のような値Tを求めることによって実施します。
$$ T = -2(\log L_0 – \log L_1)$$
検証する説明変数の数を$q$とすると、帰無仮説が正しい場合は$T$が自由度$q$ の$\chi^2$分布$\chi^2(q)$に従うことが知られているので、これを利用して検定を行います。
説明変数を性別と居住地域、目的変数を車の購入としたプロビットモデル・ロジットモデルを再度構築すると、結果は以下のようになります。
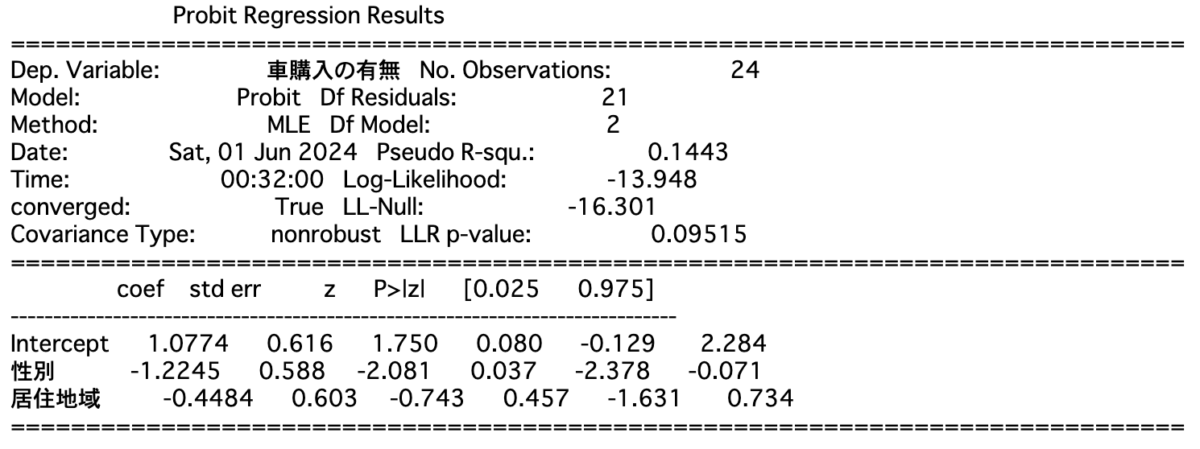
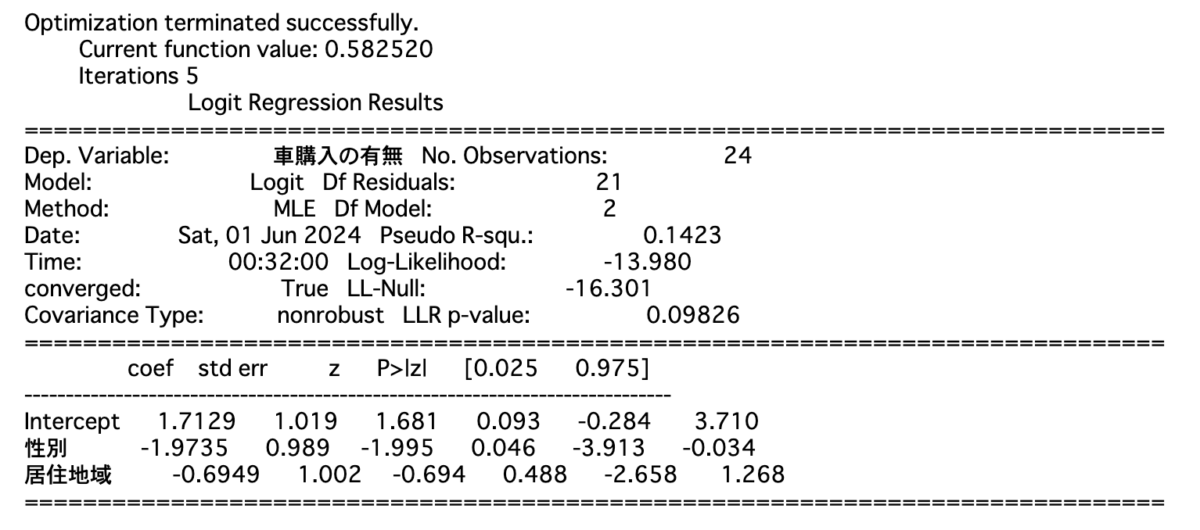
||| プロビットモデル
$$ T = -2 ( -16.301 + 13.948) = -2 \times ( – 2.353) = 4.706$$
||| ロジットモデル
$$ T = -2 ( -16.301 + 13.980) = -2 \times ( – 2.321) = 4.642$$
有意水準を5%とすると自由度$2$の$\chi^2$分布の値は$\chi^2(2) = 5.9915$であるので、プロビットモデルからもロジットモデルからも帰無仮説は棄却できないという結論が導かれます。
(iii)の解説
### (iii)
# プロビットモデルの係数を使って、回帰式を作成する
def probit_formula(income, sex, region):
y = 0.004885 * income -1.3460 * sex -0.4042 * region -1.4173
return y
# ロジットモデルの係数を使って、回帰式を作成する
def logit_formula(income, sex, region):
y = 0.009059 * income -2.3155 * sex -0.5922 * region -2.8062
return y
# 具体的な値を代入
probit = probit_formula(500, 0, 0)
# 標準正規分布の累積分布関数に代入する
pi = norm.cdf(probit)
print(f'プロビットモデルでのPi: {pi}')
### 分散を求める式が間違いの可能性あり
sigma = pi * (1 - pi)/2
print(f'プロビットモデルでの分散: {sigma}')
# 信頼区間の導出
lower = pi - 1.96 * np.sqrt(sigma)
upper = pi + 1.96 * np.sqrt(sigma)
if lower <0:
lower = 0
if upper > 1:
upper = 1
print(f'プロビットモデルによる信頼区間: [{lower}, {upper}]')
print()
# 具体的な値を代入
logit = logit_formula(500, 0, 0)
# ロジスティック分布の累積分布関数に代入する
pi = logistic.cdf(logit)
print(f'ロジットモデルでのPi: {pi}')
### 分散を求める式が間違いの可能性あり
sigma = pi * (1 - pi)/2
print(f'ロジットモデルでの分散: {sigma}')
# 信頼区間の導出
lower = pi - 1.96 * np.sqrt(sigma)
upper = pi + 1.96 * np.sqrt(sigma)
if lower <0:
lower = 0
if upper > 1:
upper = 1
print(f'ロジットモデルによる信頼区間: [{lower}, {upper}]')上記コードにおいて、漸近分布の分散を求める式が模範解答と食い違っているため、間違った解説である可能性があります。
そのため、本記事においては、問題文中の条件における確率の導出までが解説範囲とさせていただきますことをご了承いただきたいと思います。
上記コードにおいて、求めたい購入確率は以下の2ステップで求めることができます。
- それぞれのモデルで求めた係数を使って回帰式の関数を作成します
- それぞれのモデルの回帰式に具体的な値を代入する
- 回帰式の結果をそれぞれの累積分布関数に代入し、購入確率を求める
順を追って解説していきます。
それぞれのモデルで求めた係数を使って回帰式の関数を作成します
### (iii)
# プロビットモデルの係数を使って、回帰式を作成する
def probit_formula(income, sex, region):
y = 0.004885 * income -1.3460 * sex -0.4042 * region -1.4173
return y
# ロジットモデルの係数を使って、回帰式を作成する
def logit_formula(income, sex, region):
y = 0.009059 * income -2.3155 * sex -0.5922 * region -2.8062
return y先ほどデータから作成した各モデルの係数を使って、それぞれのモデルの回帰式を作成しています。
なお、値が出力結果と少し異なるのは先ほどの出力結果と本書の解答との間に有効桁数による差異があるため、上記関数の実装には本書の解答の数字を使用しているためです。
それぞれのモデルの回帰式に具体的な値を代入する
# 具体的な値を代入
probit = probit_formula(500, 0, 0)
...
# 具体的な値を代入
logit = logit_formula(500, 0, 0)各回帰式に「年収500万」「男性(=0)」「都市住み(=0)」を表す値を代入します。
回帰式の結果をそれぞれの累積分布関数に代入し、購入確率を求める
# 標準正規分布の累積分布関数に代入する
pi = norm.cdf(probit)
print(f'プロビットモデルでのPi: {pi}')
...
# ロジスティック分布の累積分布関数に代入する
pi = logistic.cdf(logit)
print(f'ロジットモデルでのPi: {pi}')回帰式のそれぞれの結果を、標準正規分布の累積分布関数
$$\Phi(\beta_0 + \beta_1 X_i) = \int_{-\infty}^{\beta_0 + \beta_1 X_i} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$$
と、ロジスティック分布の累積分布関数
$$\Lambda(\beta_0 + \beta_1 X_i) = \frac{e^{\beta_0 + \beta_1 X_i}}{1 + e^{\beta_0 + \beta_1 X_i}}$$
に代入することによって、車の購入確率を求めます。

上記計算により「年収500万円の都市住みの男性」が車を購入する確率は約84%であることがプロビットモデル・ロジットモデルから推定できました。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題5「市場調査」におけるプロビットモデル・ロジットモデルをPythonで実装し、その解き方の手順について解説いたしました!
一部ブログ主の力不足で解答が完璧ではない部分が存在いたしますが、データからプロビットモデル・ロジットモデルを構築する基礎の部分と、具体的な確率予測をする肝の部分については解説できたと認識しております。
皆さんもプロビットモデル・ロジットモデルに基づいた二値・多値予測を行う場合には本記事記載のコードをぜひ活用してみてください!




コメント