
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、ベイズ統計学がある程度学習した方がマルコフ連鎖モンテカルロ法(MCMC)の仕組みを復習するのにぴったりの書籍『モンテカルロ統計計算』から、私が得た学びを3選紹介していきたいと思います!
本書はMCMCの理論的な話がありつつ、モンテカルロ法の積分計算など、他の書籍では扱っていないトピックがありつつ、Rを実装しながら学べる、というベイズ好きにはたまらない1冊になっているので、本書の購入を考えている方はぜひ参考にしていただけると幸いです!
本書の概要
本書では、現代に至るまでベイズ統計学の中心技術であり続ける、マルコフ連鎖モンテカルロ法の実践と理解を目標とし、そのための必要な内容に絞った、いわば幹の部分の書物である.
鎌谷研吾『モンテカルロ統計計算』(講談社/2020)P vii
本書は、マルコフ連鎖モンテカルロ法(以下MCMC)について、Rの実装と理論的説明で理解していこうという書籍であり、MCMCを実装して学習する書籍の中では格段に分かりやすい1冊となっています。
以下ブログなどでは、『標準ベイズ統計学』(結構難しい)の後に位置付けられており、どんな恐ろしい書籍が来るかと戦々恐々としていたのですが、ここまで他書籍でベイズを学習してきた甲斐あってか、思いの外わかりやすい内容の書籍であることに安心したブログ主でございます。
と、いう具合に、ある程度ベイズ統計学を学んだ方であれば、既出の手法をRで実装するパターンで再学習することができるので、MCMCを深く理解するのに非常にリーズナブルな1冊となっています。
本書の構成は以下のとおりです。
- 1章 序論
- 2章 乱数
- 3章 積分法
- 4章 マルコフ連鎖
- 5章 ギフスサンプリング
- 6章 メトロポリス・ヘイスティングス法
本書から得た学び
本書から得た学びは以下の3つです
- 棄却法による乱数生成
- 不偏確率分布の一意性の議論に特異性を用いる
- マルコフ連鎖における対称性
順を追って解説していきます
棄却法による乱数生成
(擬似)乱数生成法には様々あり、書籍『自然科学の統計学』では以下のような乱数生成法が記載されています.
- M系列による線形合同法
- 乗算合同法
- 極座標法(ボックス・ミュラー法)
- 逆関数法
- 別名法
本書においては、「逆変換法」として『自然科学の統計学』の逆関数法と同様の手法が紹介されており、逆関数の計算コストが高い場合においては「近似累積分布関数による乱数生成」や逆変換法と広義な手法として「変数変換法」も紹介されています。
一方で、本書に掲載されている「棄却法」は他の書籍では乱数生成法としてはあまり見られませんが、メトロポリス・ヘイスティング法(以下MH法)のアルゴリズムと同様の乱数生成法になります。
「棄却法」は本書序盤で登場するので、モンテカルロ法における乱数生成法の1つとして頭に入れつつも、序盤で棄却法のお作法を知っておくことによって、MH法において棄却の考え方が出てきたとしてもビビらない、という作用があります。
なお、棄却法による乱数生成方法は以下のような手順です。
- 興味のある分布$P(x)$と同じ状態空間に定義された提案分布$Q(x)$を用意します
- それぞれの分布の確率分布関数$p(x), q(x)$において、以下式における$R \geqq 0 $が存在するものとします
$$r(x) = \frac{p(x)}{q(x)} \leqq R$$ - $Y \sim Q, U \sim \mathcal{U}[0,1]$を独立に生成する
- もし
$$U \leqq R^{-1}r(Y)$$
であれば、$X=Y$として終了する。そうでなければ(1)に戻る
本書はモンテカルロ法を使用した統計計算手法に主眼を置いた書籍でありつつ、すでに統計学における乱数生成法を一通り学習されている方でも、新たな乱数生成法と出会える1冊となっています。

不変確率分布の一意性の議論に特異性を用いる
マルコフ連鎖$X_0, \cdots, X_m$の長期的な振る舞いを見ていった時に、$m$を$\infty$まで飛ばしたとすると、ある一定の分布$\Pi$にたどり着くとします。
すると、その一定の分布を$X_0$(マルコフ連鎖のスタート地点)として改めて置き直すと、$X_0$は分布$\Pi$に従っていると言えます。(なぜならそうなるように置き直したからです)
すると、次のマルコフ連鎖先$X_1$も「一定の分布」になっているはずなので、$X_1$も分布$\Pi$に従っているはずです。
このような、マルコフ連鎖$X_m$が最終的にたどり着くような分布のことを、「極限飛ばすとそこから分布変わんないじゃん」ということで不変確率分布と表します。
この不変確率分布ですが、マルコフ連鎖によっては不変確率分布が複数存在する可能性があります。
例えば、「コインの表裏に賭けて、どちらかの財産がなくなるまで1,000円を取引し合う」という闇のゲームを開催した場合は、「自分が勝負に勝つ確率$p(x)$」の確率分布として以下の2パターンが考えられます。
- 自分が所持金が0になった場合は、その後は自分は必ず負けるので$p(x) = 0$
- 相手の所持金が0になった場合は、その後は自分は必ず勝つので$p(x) = 1$
※前提条件からして、「なぜ闇のゲームが終わっていないんだ、、、?」と不思議かもしれませんが、一旦飲み込んでください
上記のように、不変確率分布は複数存在する可能性がありますが、どういった時に不変確率分布は一意に(これ1つだけだ!)と定まるのでしょうか?
その疑問について、本書では特異性という概念を取り入れて説明をしていきます。
特異性とは?
二つの確率分布$P, Q$に対し、ある集合$A$があって、
$$P(A) = 0, Q(A^C) = 0$$
となる時、$P$と$Q$は互いに特異であるといい、$P\perp Q$と書く。
また互いに特異でないとき$P\not \perp Q$と書く。
上記定義だけではちんぷんかんぷんなのですが、図にすると「赤い領域が存在していると$P$と$Q$は特異じゃないよ」と認識してください。
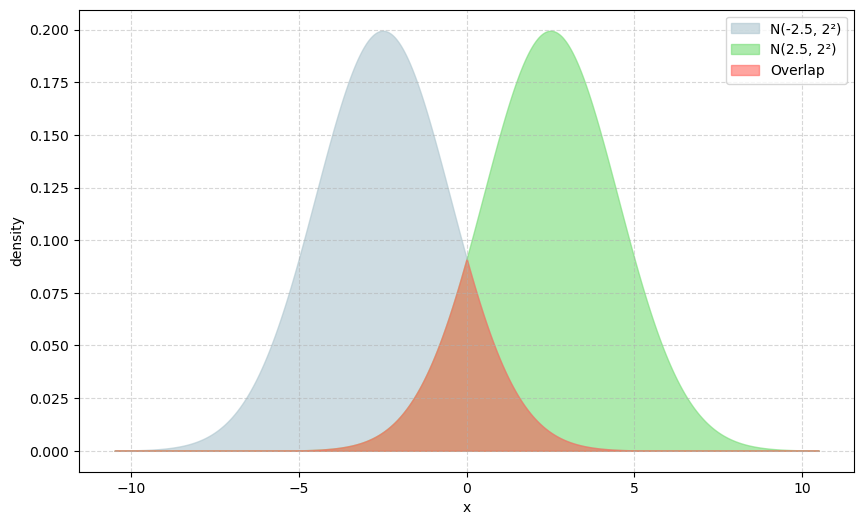
そして、本書のその後の展開としては
- どのような状況であれば、$P$と$Q$は特異でないのか
- スタート地点の少し異なる$P(x, \cdot)$と$P(y, \cdot)$があったとして、それらが特異でないなら、不変確率分布が存在した場合は一意に決まる
のような形で、不変確率分布の一意性を示していきます。
他のベイズ統計学や計量時系列分析の本では、「定常性」「定常分布」については取り上げていたものの、「特異性」については取り上げていなかったので、本書から得た新しい学びでした。
マルコフ連鎖における対称性
先ほどは不変確率分布$\Pi$の話を少ししましたが、実は$\Pi$の不変性を示すのは難易度が高かったりします。
そのため、本書では$\Pi$-不変を簡単にチェックできるケースとして、$\Pi$-対称性について紹介しています。
対称分布とは?
確率分布$\Pi$で、$X_0$が$\Pi$に従うとき、$X_0, X_1$の同時分布と$X_1, X_0$の同時分布が等しいなら、$\Pi$を$P$の対称分布といい、$P$を$\Pi$-対称という。
そして、$\Pi$-対称であれば$\Pi$-不変であることは非常に簡単に証明されます。
本書の記載によれば、
「MCMCでは、よく使われるものは$\Pi$-対称性を持つ」
「$\Pi$-対称ではないMCMCも$\Pi$-対称なマルコフカーネルの組み合わせや拡張によって作られるものが多い」
とのことなので、不変分布を持つようなMCMCを設計したい場合は、$\Pi$-対称性を持つように分布を設定してあればいいことがわかります。
$\Pi$-対称性についても他の書籍では扱われていなかったので、本書で得た学びとして入れさせていただきました。

まとめ
今回の記事では、ベイズ統計学がある程度学習した方がマルコフ連鎖モンテカルロ法(MCMC)の仕組みを復習するのにぴったりの書籍『モンテカルロ統計計算』から、私が得た学びを3選紹介させていただきました!
ベイズ統計学の書籍は数あれど、それぞれの書籍が微妙にカバーしている範囲は異なっているので、複数の書籍を読み進めていくうちに新たな発見があり、非常に楽しいので、本記事を読んで興味の湧いた方はぜひ購入してみてください!




コメント