差分方程式から破産確率の一般項の導出する過程を丁寧に解説してみた

元教師

こんにちは！データサイエンティストの青木和也（https://twitter.com/kaizen_oni）です！

今回の記事では、破産確率の一般項を導出してみたいと思います！

破産確率の導出には差分方程式の解き方が必要になってくるので、差分方程式の解法についても丁寧に解説をしていきたいと思います！

モチベーション
問題設定
解説
まとめ

モチベーション

破産確率の一般項$r(a)$は統計学の青本「自然科学の統計学」の第10章確率過程の基礎に以下のように書かれています。

$$r(a) = \frac{(q/p)^N – (q/p)^a}{(q/p)^N – 1}~~~(p \ne qのとき)$$

$$r(a) = 1 – \frac{a}N ~~~(p = qのとき)$$

ですが、この式を導出するための途中式はなく、ただ一文だけ「差分方程式を解くと」とのみ書かれています。

ちなみに、差分方程式を解くと、以下のような式が出てきます。

$$ x = \frac{1 \pm \sqrt{1 – 4pq}}{2p}$$

…どう考えても、$r(a) = \frac{(q/p)^N – (q/p)^a}{(q/p)^N – 1}~~~(p \ne qのとき)$には収束しなさそうに見えますよね？？

そこで、本記事にて破産確率$r(a)$の導出過程を丁寧に記載し、本書の「差分方程式を解くと」で置いてきぼりにされた読者を救済したいと考えております。

差分方程式とは？

差分方程式とは、数列$\{a_n\}$に対する項間の漸化式

$$a_{n+2} + pa_{n+1} + qa_n = 0, ~~~n = 0, 1, \cdots$$

の一般項$a_n$を求めるとした場合の上式のことを指す。

問題設定

まずは、破産確率$r(a)$を求めるための問題設定を見ていきましょう。

AとBの2人がいて、最初にAが$a$枚、Bが$N-a$枚のチップを持っていたとしよう。（つまり場の合計チップ数は$N$枚で一定）

コインを投げ続け、表が出た時にはAがBから1枚チップをもらい、逆に裏が出た時には、AがBに1枚チップをあげるとする。

コインの表が出る確率を$p$、裏が出る確率を$q(=1-p)$として、Aが破産する確率$r(a)$を求めよう。
参照: 東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第10章 P280

例えば、Aの初期チップ数が$3$枚、Bの初期チップ数が4枚、場には合計7枚のチップがあるような時、コインの表が出る確率が$\frac12$と仮定すると、Aのチップの枚数の推移は以下図のようにシミュレーションすることができます。

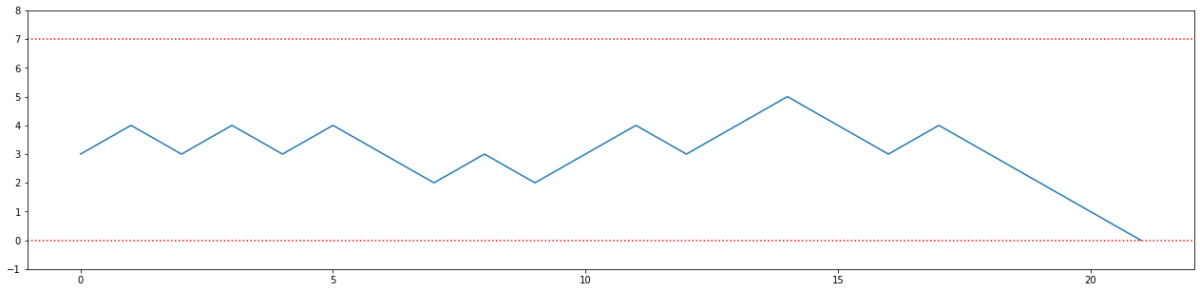
下の赤い点線に触れた場合にはAが0枚、Bが7枚チップを所持した状態なので、Aが破産となります。

逆に上の赤い点線に触れた場合はAが7枚、Bが0枚チップを所持した状態なので、Bが破産となります。

そして、この破産のしやすさはAの初期チップ数$a$と場全体のチップ数$N$によって変動します。

例えば、Aの初期チップ数が5枚で、Bの初期チップ数が15枚の場合には、Bは少なくとも5回勝てばAを破産に追い込むことができますが、Aは少なくとも15回は勝たなければBを破産に追い込むことができないので、Aが非常に不利な状況となっています。

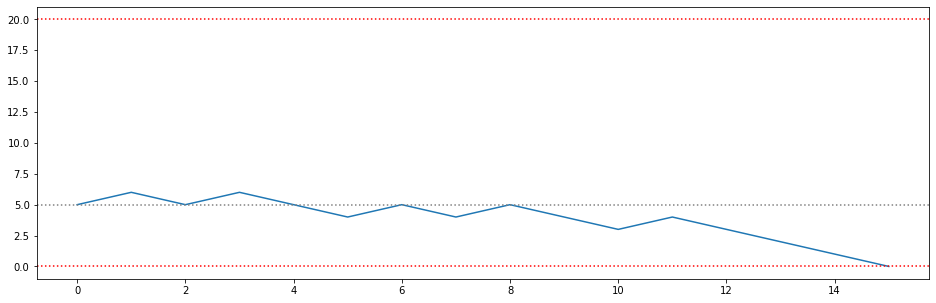
この$a$と$N$に依存する破産確率$r(a)$を求めることが本記事のゴールです。

なお、以下が上記資産推移を導出するコードです。

import numpy as np
import random
import math
import matplotlib.pyplot as plt

a = 5
A = [a]
N = 20
p = 1/2
t = 0
times = [t]

while True:
    number = random.random()
    if number >= p:
        a += 1
        print('表')
    else:
        a -= 1
        print('裏')
    A.append(a)
    t += 1
    times.append(t)
    if a == 0:
        print(f'Aは破産しました')
        break
    elif a == N:
        print(f'Bは破産しました')
        break
        
plt.figure(figsize = (len(A), 5))
plt.plot(times, A)
plt.axhline(N, ls = 'dotted', c = 'red')
plt.axhline(0, ls = 'dotted', c = 'red')
plt.axhline(A[0], ls = 'dotted', c = 'gray')
plt.ylim(-1,N+1)

解説

破産確率$r(a)$を求める問題を以下の3ステップで解いていきましょう

差分方程式（=漸化式）を導出する
境界条件を確認する
差分方程式を特性方程式を使って解く

順を追って解説していきましょう。

特性方程式とは？

特性方程式とは、(2次の)差分方程式$a_{n+2} + pa_{n+1} + qa_n = 0$に対する以下の方程式

$$t^2 + pt + q = 0$$

のことを指す。

特性方程式を解いて得られた解を$\alpha, \beta (\alpha \ne \beta)$とすると、任意の定数$A, B$を用いて、

$$a_n = A\alpha^n + B\beta^n$$

が求めるべき差分方程式の一般項$a_n$となる。

また、特性方程式の解が重解$\alpha$のみとなる場合には、

$$a_n = (A + Bn)\alpha^n$$

が求めるべき差分方程式の一般項$a_n$となる。

なお、定数$A, B$の値は境界条件より求めることができる。

差分方程式（=漸化式）を導出する

まずは、破産確率$r(a)$の差分方程式を導出します.

ここで、事象R, Hを以下のように定めます。

$$R=\{Aがいつか破産する\}, H=\{第１回目にコインの表が出る\}$$

そして、我々が求めたい破産確率は$r(a)$は$P(R)$のはずです。

なお、事象$R$について考えると、第１回目に表が出ても裏が出ても、事象がRが起こる（=Aが破産する）ことはありうる、かつ第１回目に表が出る事象$H$と裏が出る事象$H^C$は排反事象である（=同時に起こることはない）ことから、以下のような式が成り立つはずです。

$$R = (R\cap H) \cup (R \cap H^C), ~~~ (R\cap H) \cup (R \cap H^C) = \Phi$$

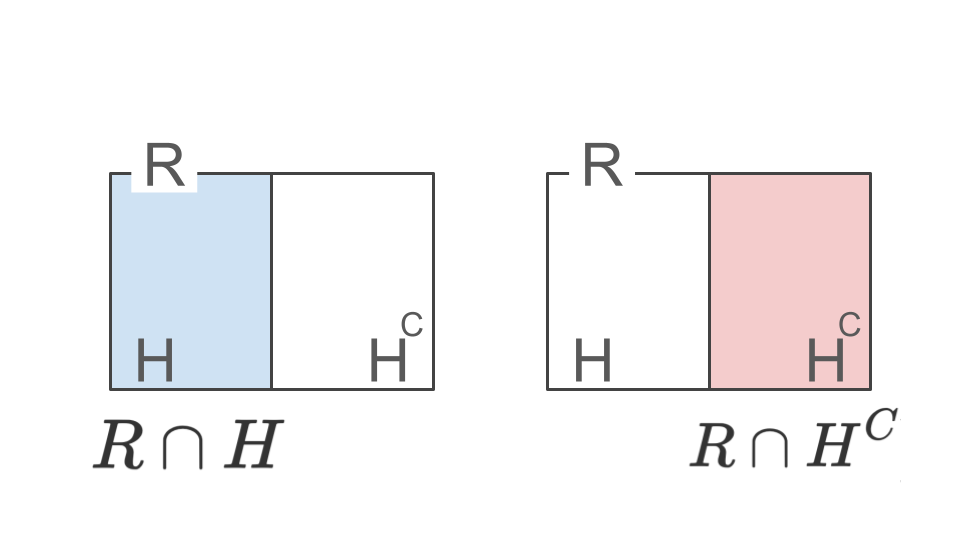
すると、破産確率$P(R)$について、以下のように表現することができます。

$$P(R) = P(R\cap H) + P(R \cap H^C)$$

そして、条件付き確率の式より、$P(R\cap H)$と$P(R\cap H^C)$のそれぞれを次のように変形することができます。

$$P(R\cap H) = P(R|H)P(H)$$

$$P(R\cap H^C) = P(R|H^C)P(H^C)$$

ここで、上式に出てくるそれぞれの確率は以下のように$p, q, r(a)$を使って表現することが可能です。

第１回目に表が出る確率$P(H) = p$
第１回目に裏が出る確率$P(H) = q$
第１回目に表が出た状況において、Aが破産する確率$P(R|H) = r(a+1)$
第１回目に裏が出た状況において、Aが破産する確率$P(R|H^C) = r(a-1)$

$r(a+1)$について詳述すると、第１回目に表が出た場合には、Aのチップは$a$から$a+1$に増加しますが、次の回を再度第１回目とすると、Aはチップ$a+1$枚からのスタートとなります。

すると、考えるべき破産確率はAがチップ$a+1$枚からスタートした時の破産確率になるので、$r(a+1)$と表現できることになります。

先ほど求めた確率$P(H), P(H^C), P(R|H), P(R|H^C)$をそれぞれ$P(R)$を求める式に代入すると

$$P(R) = r(a+1) \times p + r(a-1) \times q = pr(a+1) + qr(a-1)$$

よって、差分方程式

$$r(a) = pr(a+1) + qr(a-1)$$

を得ることができます。

境界条件を確認する

さて、この後差分方程式の特性方程式を使って一般項$r(a)$を求めていくのですが、一般項を求めるためには初期条件（=境界条件）が必要となります。

この時考えるべきは以下の2シチュエーションです。

Aの所持チップ数が0枚になった時の破産確率$r(0)$
Aの所持チップ数が$N$枚になった時の破産確率$r(0)$

まず、$r(0)$について考えると、所持チップ数0枚は明らかに破産しているので、破産確率は$100%$です。

よって、$r(0) = 1$となります。

一方、Aの所持チップ数$N$枚の場合は、Bの所持チップ数が0になっていることと同義なので、Aが破産することは絶対にあり得ません。

よって、$r(N) = 0$となります。

差分方程式を特性方程式を使って解く

さて、すべての準備が整ったところで、差分方程式$r(a) = pr(a+1) + qr(a-1)$から一般項$r(a)$を求めていきましょう。

一般項を求めるためには、次の3ステップの手順を踏みます。

特性方程式の解を求める
$p \ne q$の場合における一般項を求める
$p = q$の場合における一般項を求める

順を追って解説していきます。

特性方程式の解を求める

先ほどの差分方程式を整理すると次のようになります。

$$pr(a+1) – r(a) + qr(a-1) = 0$$

よって、差分方程式から次のような特性方程式が導かれます。

$$px^2 – x + q = 0$$

これを2次方程式の解の公式を使って解くと、$x$の値は次のようになります。

$$x = \frac{1 \pm \sqrt{1 – 4pq}}{2p}$$

ここで、$q = 1-p$を利用すると

$$x = \frac{1 \pm \sqrt{1 – 4p(1-p)}}{2p} = \frac{1 \pm \sqrt{4p^2 – 4p + 1}}{2p}$$

$$ = \frac{1 \pm \sqrt{(2p-1)^2}}{2p} = \frac{1 \pm |2p-1|}{2p}$$

$$ = \frac{1 \pm |p + p -1|}{2p} = \frac{1 \pm |p – (1-p)|}{2p} = \frac{1 \pm |p-q|}{2p}$$

$p \ne q$の場合における一般項を求める

$x = \frac{1 \pm |p-q|}{2p}$について、$p>q$であっても$p<q$であっても、

$$\pm |p-q| = \pm (p-q)$$

であることから、

$$ x = \frac{1 \pm |p-q|}{2p} = \frac{1 \pm (p-q)}{2p} = \frac{1+ p-q}{2p},\frac{1- (p-q)}{2p} $$

$$ = \frac{p + 1-q)}{2p},\frac{1- p + q)}{2p} = \frac{2p}{2p}, \frac{2q}{2p} = 1, \frac{q}p$$

よって、差分方程式の一般解は

$$r(a) = A\cdot 1^a + B\cdot \left(\frac{q}p \right)^a = A + B\left(\frac{q}p \right)^a$$

ここで、境界条件$r(0) = 1, r(N) = 0$を利用すると

$$r(0) = A + B = 1$$

$$r(N) = A + B\left(\frac{q}p \right)^N = 0$$

よって,$r(0)-r(N)$より、

$$B= \frac{1}{1 – \left(\frac{q}p \right)^N}$$

が得られ、$A = -B\left(\frac{q}p \right)^N$より

$$A= \frac{-\left(\frac{q}p \right)^N}{1 – \left(\frac{q}p \right)^N}$$

が得られる。

よって、求める破産確率$r(a)$は

$$r(a) = \frac{- \left(\frac{q}p \right)^N + \left(\frac{q}p \right)^a}{1 – \left(\frac{q}p \right)^N} = \frac{\left(\frac{q}p \right)^N – \left(\frac{q}p \right)^a}{\left(\frac{q}p \right)^N -1}$$

これは、「自然科学の統計学」第10章P280に記載の式と一致する