
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の基本の「き」、相関係数について解説していきたいと思います!
相関係数は身長と体重など、データ間の関係性を読み解くのに非常に重要な指標です。
一方で、世の中では「相関」について誤った認識が出回ってしまっている印象があります。
まずは本記事で相関係数を定義からしっかり叩き込みましょう!
相関とは
まずは相関係数について考える前に、そもそも相関とはなんぞや、という部分について切り込んでいきましょう!
例えば、「身長が高い人ほどモテる」という説について、あなたはどう思うでしょうか。

そりゃ女子はみんな自分より身長が高い人の方が好きに決まってるから、身長が高い人の方がモテるに決まってるじゃん!

いやいや、身長みたいな身体的特徴でモテるのは大学生までで、社会人になったら年収とか他の軸で評価されるから身長とモテとは無関係だよ!

いやいや、身長よりも体脂肪率の方が大事だよ!今は韓国アイドルとかが流行ってる時代だから、体脂肪率の低いスリムの男子がモテるんだって!
以上のようにさまざまな意見があるかもしれません。
それでは、男性Aが主張するように「身長が高いとモテる」という説が正しいと仮定してみましょう。
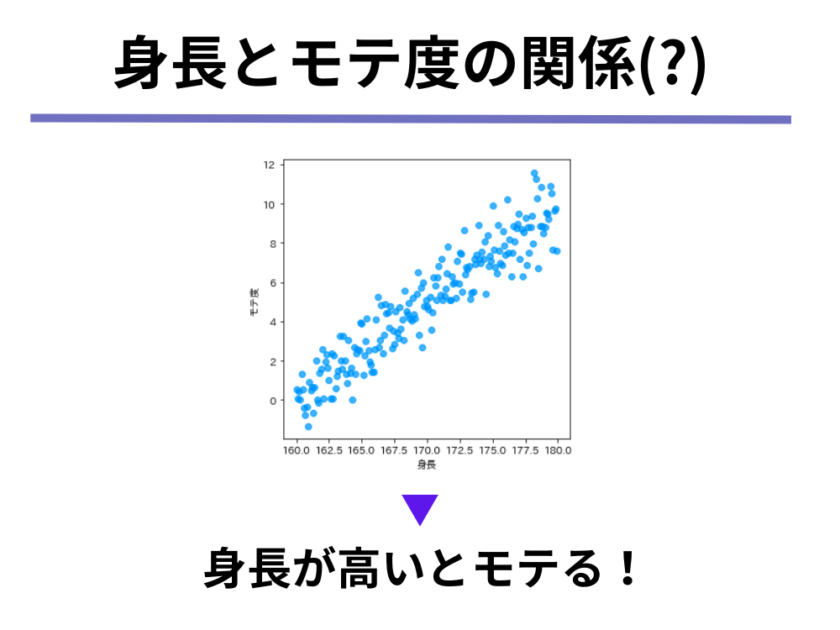
すると、「身長」と「モテ度」なる謎の指標の関係性を可視化すると、以下のような図になるのはイメージがつきますでしょうか。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import random
height = np.arange(160,180,0.1)
love = np.arange(0, 10, 0.05) + [random.normalvariate(mu = 0, sigma = 1) for i in range(200)]
fig = plt.figure(figsize = (5,5))
plt.scatter(height, love, c = '#1E90FF', alpha = 0.7)
plt.xlabel('身長')
plt.ylabel('モテ度')上の図を見ると、多少のばらつきはあるものの「身長が高くなればなるほど、モテ度も上がる」という関係が成り立っています。
上の図のように、「一方が増えればもう一方も増える」ような関係が2つの変数(この場合は身長とモテ度)にある時、2つの変数について正の相関関係があると表現します。
一方で、男性Bの主張「身長とモテ度は無関係」という説が正しいと仮定してみましょう。
すると、「身長」と「モテ度」の図は以下のようになります。
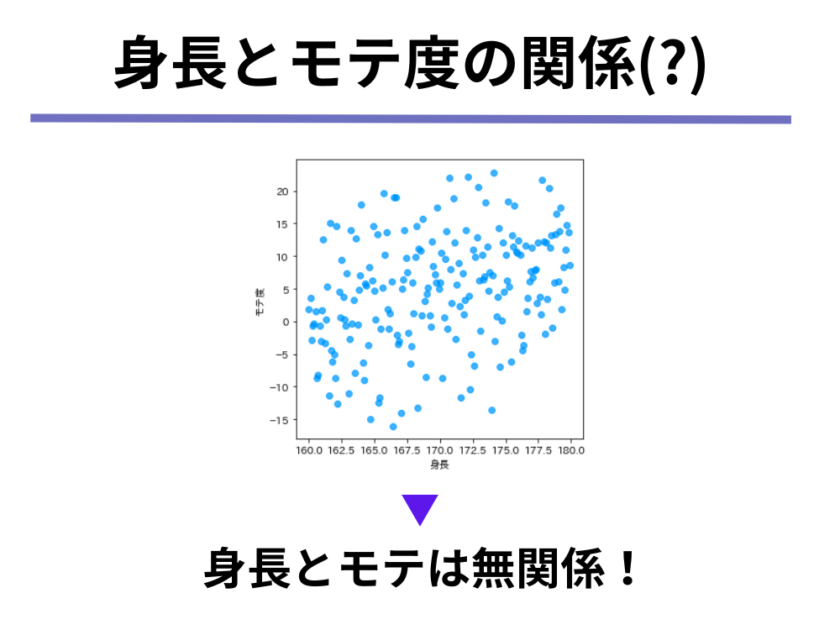
上の図のように、2つの変数の間に「一方が増えればもう一方も増える」「一方が増えればもう一方は減る」のような関係性が見られないとき、相関関係がないと表現します。
最後に、男性Cの主張「体脂肪率が低い方がモテる」という説が正しいと仮定してみましょう。
すると、「体脂肪率」と「モテ度」は以下の図のような関係にあるのがお分かりになりますでしょうか。
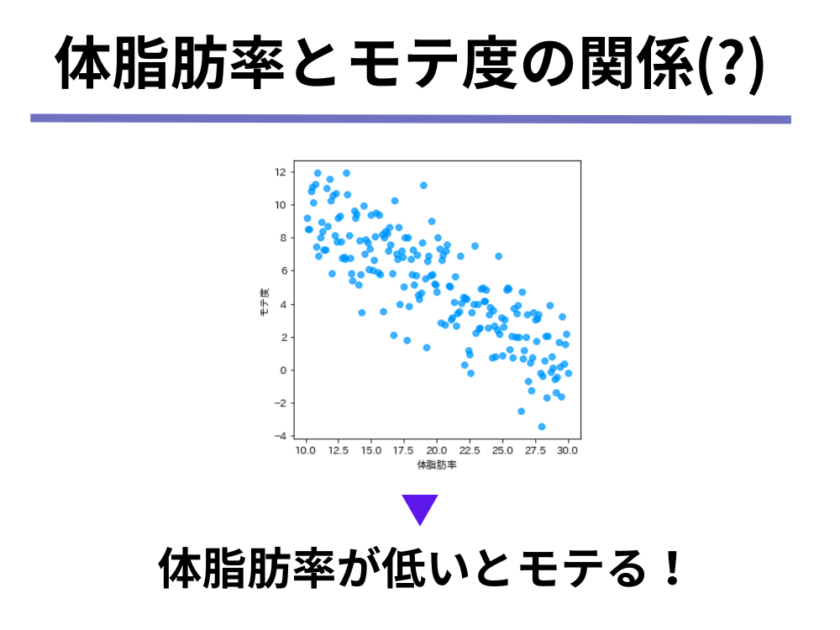
上の図のように、「一方が増えれば、一方は減る」ような関係が2つの変数(今回の場合は「体脂肪率」と「モテ度」)にあるとき、2つの変数について負の相関関係があると表現します。
以上のように、相関関係とは2つの変数がどんな関係にあるのかを表すものだ、ということを覚えておきましょう!
相関係数とは?
ここまでで「相関」についてはなんとなく理解いただけたかと思います。
ここで記事冒頭で出てきた相関関係とは、一体何を表すのでしょう?
ここで、以下の問いについて考えてみてください。
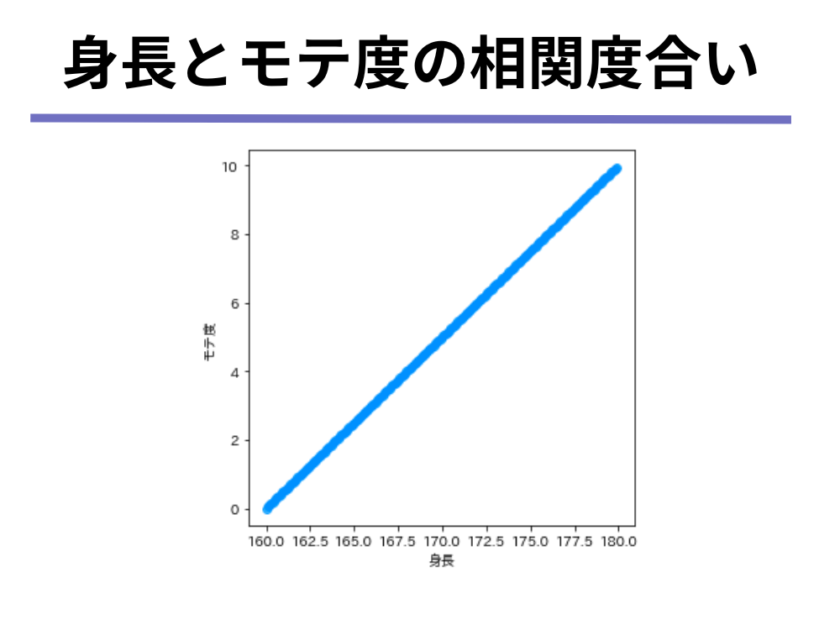
身長とモテ度が以下の図のような関係にあるとき、相関の度合いを%で表すと、あなたは何%相関していると表現しますか?
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import random
height = np.arange(160,180,0.1)
love = np.arange(0, 10, 0.05)
fig = plt.figure(figsize = (5,5))
plt.scatter(height, love, c = '#1E90FF', alpha = 0.7)
plt.xlabel('身長')
plt.ylabel('モテ度')いかがでしょうか。
上の図の相関度合いについては多くの人が「100%相関している」と答えたかと思います。
さて、それではここで上記の図の相関度合いを相関係数を使って表現してみます。
すると、以下のようになります。
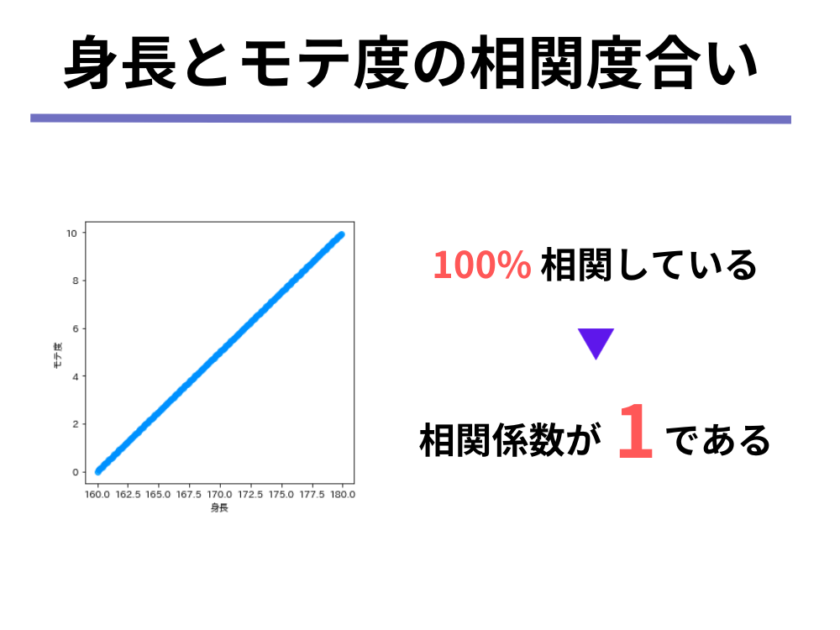
そう、思い出した方もいるかもしれませんが、小学校の頃の算数で、5%のことを0.05と変換したり、110%のことを1.1と変換して計算を行なっているように、相関係数というのは「相関の度合い」を%ではない表現で表したものなのです。
それでは、続いて次の問いにも答えてみましょう。
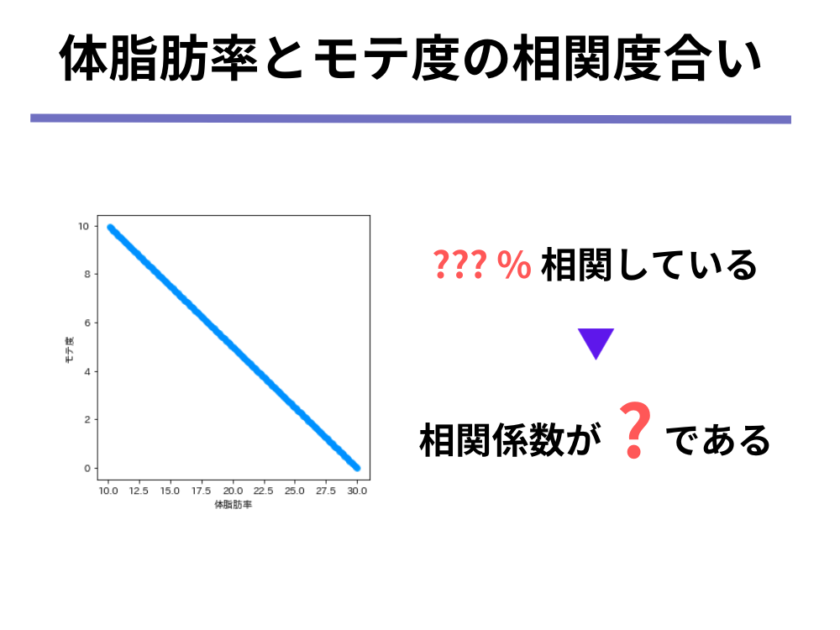
次の(1)身長とモテ度、(2)体脂肪率とモテ度が以下のような関係にある時、あなたなら何%相関していると表現しますか。また、その時の相関係数の値を答えてください。
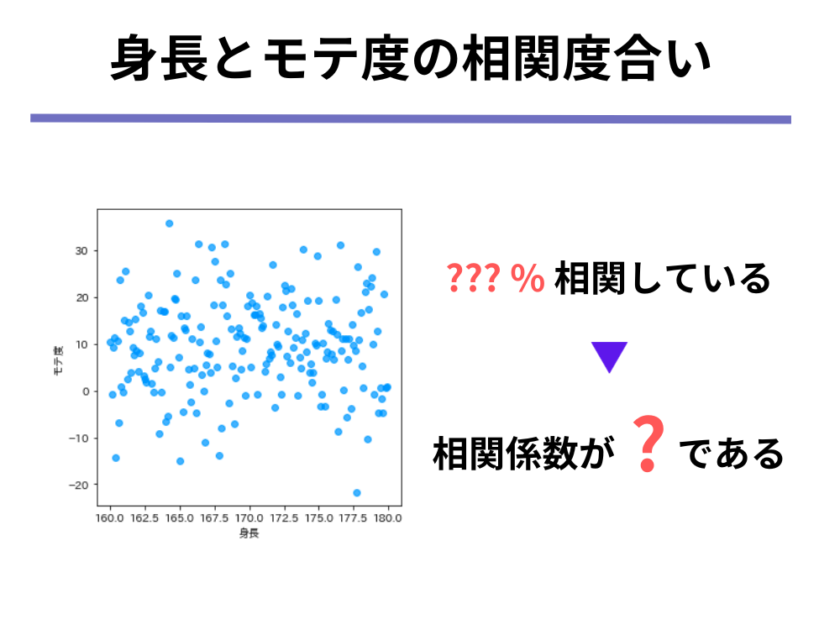
(1)身長とモテ度については、一方が増えればもう一方も増える、または一方が増えれば一方は減る、のような関係性は成り立っていないように思えます。
よって、相関関係がないと言えるので、そのような場合には「0%相関している」(=つまり相関していない)と言えるのではないでしょうか。
すると、0%を%ではない表現で表すと、そのまま0となります。
よって相関係数は0ということができます。
(2)体脂肪率とモテ度については、「体脂肪率が増えるとモテ度は下がる」ということが明らかですね。
そうした場合は「負の相関関係がある」というのでしたね。
さて、それでは負の相関は何%ということができるでしょうか。
すでに感の良い方はお気づきかもしれませんが、「負の相関関係」とあるように、相関の度合い並びに相関係数は負の値を取ることができます。
そう考えると、体脂肪率とモテ度の関係は体脂肪率が増えると必ずモテ度は減少するので、「-100%相関している」ということができるのではないでしょうか。
ここで、「-」をつけているのは「増えたら増える」(=正の相関関係)の時は「+100%」で表現したことと矛盾しないようにするためです。
そして、「-100%相関している」を相関係数に変換すると-1となります。
さて、相関係数についてまとめに入りましょう。
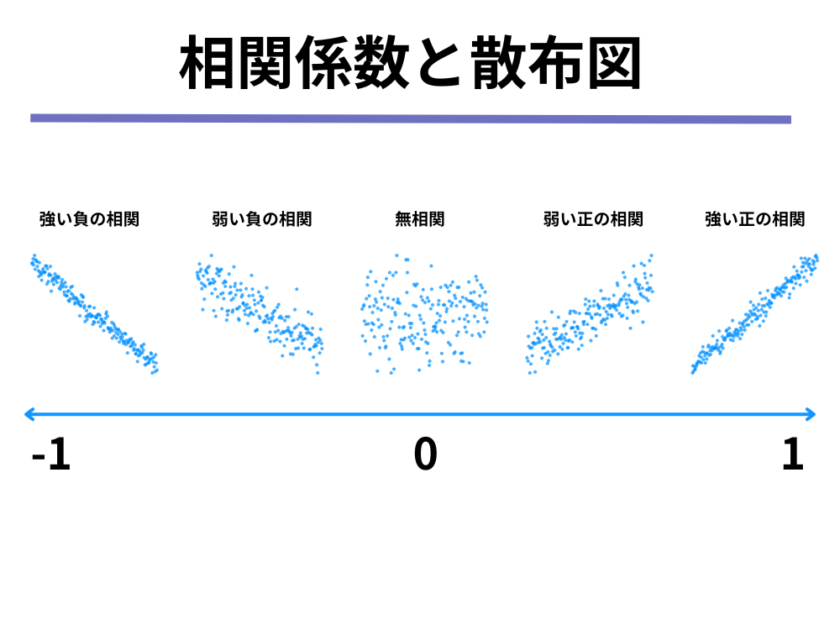
上の例によると相関の度合いは「-100%から100%」で表すことができ、相関係数についても同様に「-1から1」までの数値で表すことができます。
そのことを散布図と一緒にまとめると以下のようになります。
相関係数は2つの変数の相関の度合いを表し、-1〜1の間の値を取ります。
相関係数の定義
それでは、相関係数について直感的に理解していただいたところで、次に相関係数の定義について見ていきましょう。
相関係数は次の式によって求めることができます。
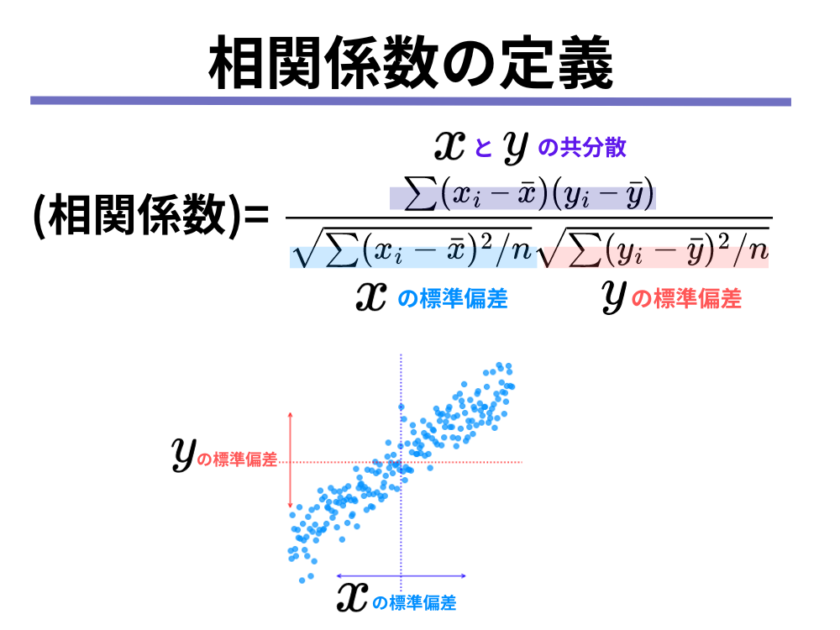
※実は相関係数には様々な定義があり、今回紹介しているのはその中でも最も一般的に用いられるピアソンの積率相関係数を紹介しています。
さて、相関係数の定義式について丁寧に追っていきましょう。
まずは分子を見てみると、「各データ[mathjax]\(x_i\)から平均[mathjax]\(\bar{x}\)を引いたもの」と「各データ[mathjax]\(y_i\)から平均[mathjax]\(\bar{y}\)を引いたもの」のかけ算を足し合わせたものであることが分かります。
これを共分散と言います。
記号[mathjax]\(\sum\)は「後ろのものを全て足す」ということを意味します。
なので今回の場合は、[mathjax]\(\sum\)の後ろにある[mathjax]\((x_i-\bar{x})(y_i-\bar{y})\)を全て足すことにつながるのです。

この共分散は何を表しているのでしょうか。
実はこの共分散はこれまで話してきた相関と同様に「一方が大きくなる時、もう一方は大きくなるのか、小さくなるのか、それとも全然関係ないのか」をダイレクトに表す値です。
それでは、共分散の値について、以下の3つのパターンに分けてみていきましょう。
- 共分散がプラスの値になるパターン
- 共分散がマイナスの値になるパターン
- 共分散が0になるパターン
共分散がプラスになるパターン
共分散がプラスになるのは「[mathjax]\( (x_i – \bar{x})\)と[mathjax](y_i – \bar{y})\)が揃ってプラスまたはマイナスであるような[mathjax]\( x_i, y_i \)の組み合わせが多いとき」です。
[mathjax]\( (x_i – \bar{x})\)と[mathjax](y_i – \bar{y})\)が揃ってプラスまたはマイナスになると、それら2つのかけ算の結果である[mathjax]\( (x_i – \bar{x})\)(y_i – \bar{y})\)はプラスになります。
すると、プラスばかり多く足されるので、共分散[mathjax]\( \sum(x_i – \bar{x})\)(y_i – \bar{y})\)もプラスになるのです。
ここで、[mathjax]\( (x_i – \bar{x})のプラスになる時・マイナスになる時、[mathjax](y_i – \bar{y})\)のプラスになる時・マイナスになる時を図を使いながら個別に考えていきましょう。
まずは、[mathjax]\( (x_i – \bar{x}) \)のプラスになる時・マイナスになる時ですが、[mathjax]\(x_i\)が[mathjax]\(x\)全体の平均[mathjax]\(\bar{x}\)より大きい時がプラス、小さい時がマイナスと考えられるので、以下の図のようになることが分かります。
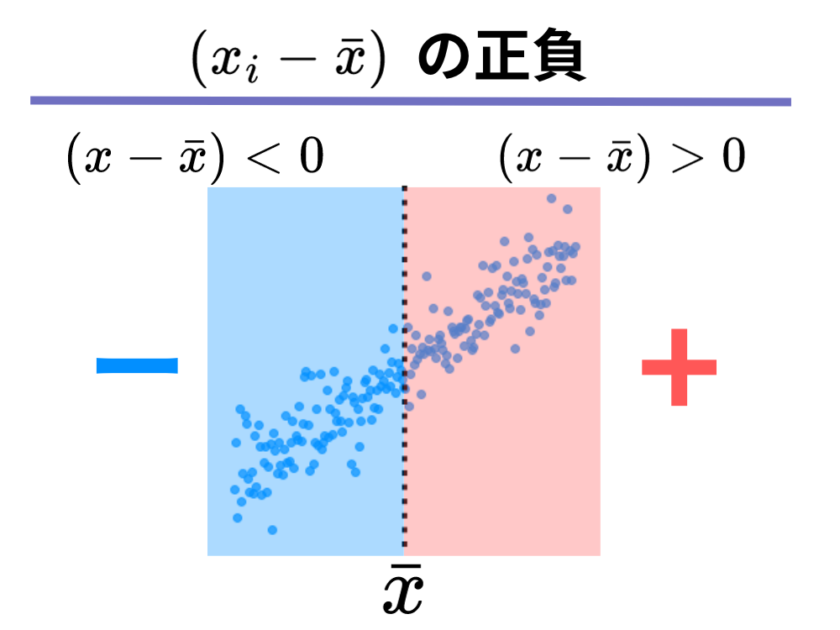
まずは、[mathjax]\( (y_i – \bar{y}) \)のプラスになる時・マイナスになる時ですが、[mathjax]\(x\)の場合と同様に以下の図のようになることが分かります。
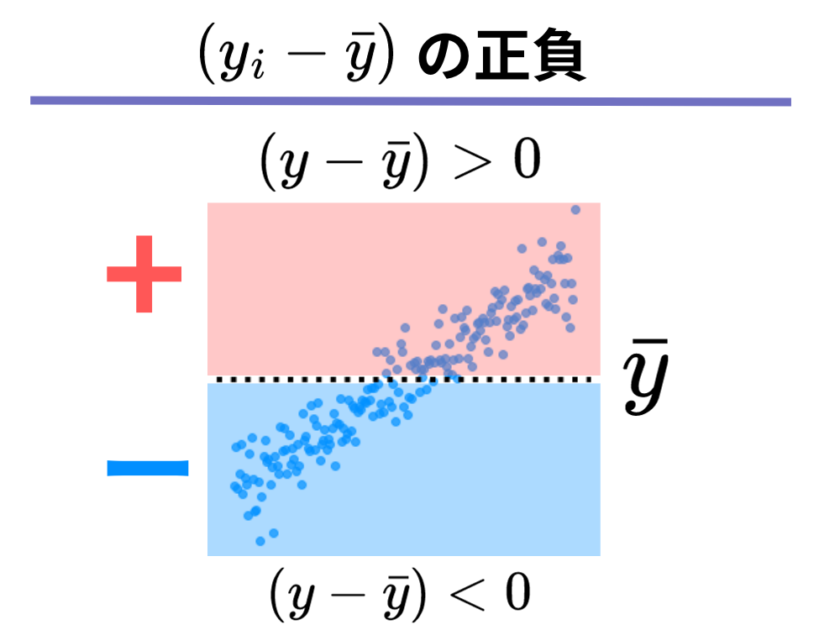
上記の2つの図を踏まえて考えると、「mathjax]\( (x_i – \bar{x})\)と[mathjax](y_i – \bar{y})\)が揃ってプラスまたはマイナスになる時」というのは、どことどこのエリアを指しているのかお分かりになったでしょうか。
そうです、以下の図のようにグラフの右上と左下のエリアが「mathjax]\( (x_i – \bar{x})\)と[mathjax](y_i – \bar{y})\)が揃ってプラスまたはマイナスになる」エリアになります。
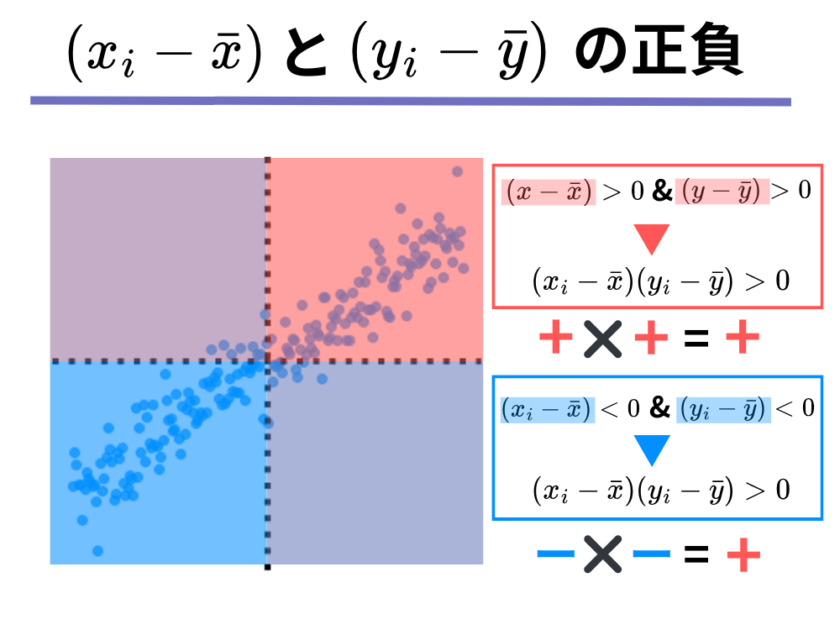
そして、右上のエリアと左下のエリアにデータが多くあるような散布図はどのような散布図でしょうか。
そう、あなたが想像している通り、左下から右斜め上に向かってデータの点が横断しているような、右肩上がりの散布図であることが分かるかと思います。
そのような散布図は、[mathjax]\( x\)軸方向(横方向)に増えると、[mathjax]\( y\)軸方向(縦方向)は増加するような散布図であることが分かるので、「一方が増えればもう一方が増える」、つまり、正の相関関係にあることが分かります。
共分散がマイナスになるパターン
先ほどとは逆に、共分散がマイナスになるパターンとはどのような時でしょう。
共分散がマイナスになる時は、「[mathjax]\( (x_i – \bar{x})\)と[mathjax](y_i – \bar{y})\)のかけ算の結果がマイナスになる2つの値[mathjax]\(x_i, y_i \)の組み合わせが多い時」です。
ここで、2つの数のかけ算がマイナスになる時はどんな時かを思い出してみましょう。
そうですね、一方がプラスの値で、もう一方がマイナスの値のときに、2つの数のかけ算はマイナスになるのでした。
(一方がプラスで、もう一方がマイナス、、、?どこかで聞いた覚えのあるような、、、)
さて、先ほどの図をもう一度見返してみると、「一方がプラス、一方がマイナス」のエリアはどこのことを指しているのはお分かりになりますでしょうか。
そうですね、以下の図のように左上のエリアと右下のエリアが「一方がプラスで、もう一方がマイナス」のエリアになります。
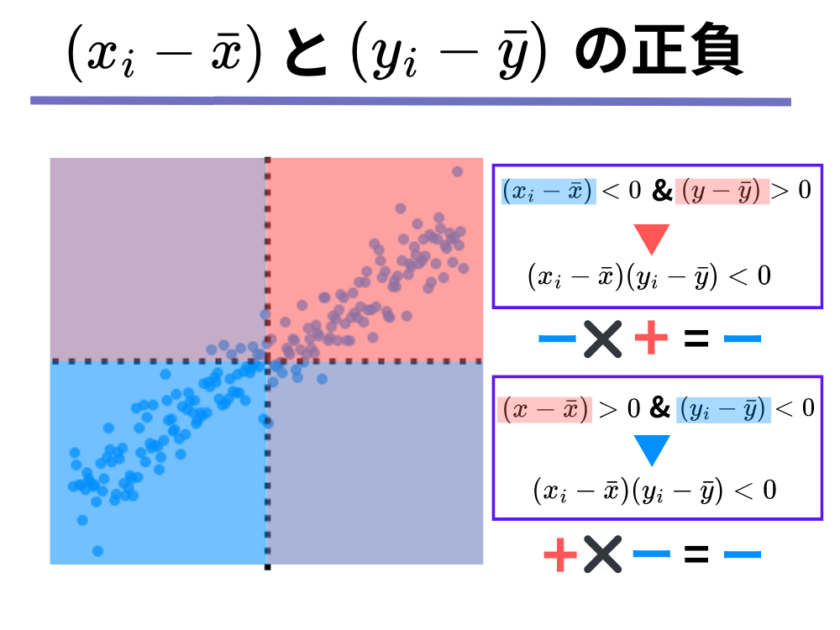
そして、左上のエリアと右下のエリアに多くデータが存在するような散布図とは、どのような散布図かイメージしてみてください。
そうです!あなたの想像した通り、以下の図のような左上から右斜め下に向かってデータの点が分布しているような、右肩下がりのグラフであることが分かります。
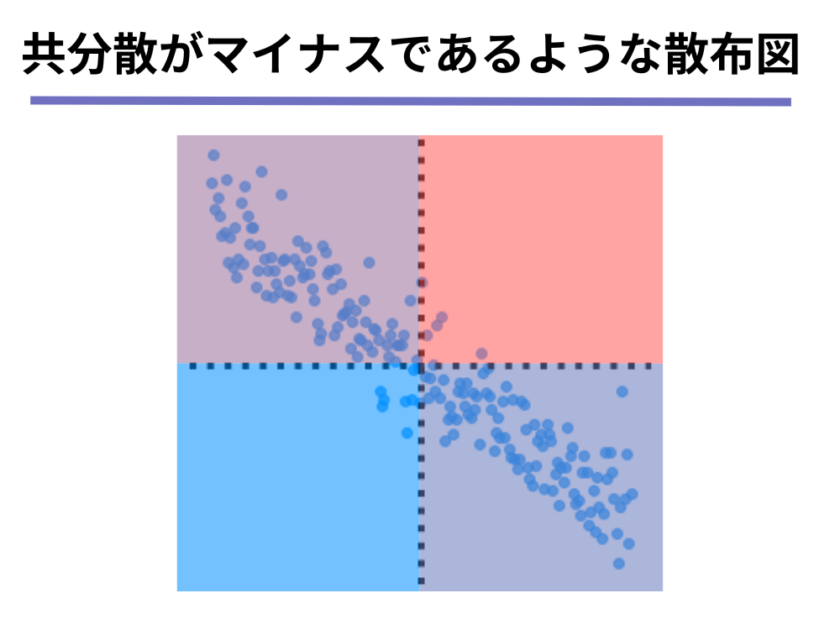
そのような散布図は、[mathjax]\( x\)軸方向(横方向)に増えると、[mathjax]\( y\)軸方向(縦方向)は減少するような散布図であることが分かるので、「一方が増えればもう一方が減る」、つまり、負の相関関係にあることが分かります。
共分散が0のパターン
ここまでで共分散がプラスのパターンとマイナスのパターンについて見てきました。
一方、相関関係には「正の相関関係」「負の相関関係」とは別に「相関関係なし」という状態があることを学びました。
そして「相関関係なし」に対応するのが、「共分散の値が0になるパターン」です。
それでは、まずはどのような時の共分散の値が0になるのか考えてみましょう。
そもそも共分散とは以下の式で計算される値でした。

それではまずはものすごく極端な例を考えてみましょう。
例えば、データが[mathjax]\( x_1, y_1 \)と[mathjax]\( x_2, y_2 \)の2点しかないと仮定してください。
このようなときに以下の領域のどことどこに[mathjax]\( x_1, y_1 \)と[mathjax]\( x_2, y_2 \)を配置すれば共分散は0になるでしょうか?
なお、[mathjax]\( \bar{x}, \bar{y} \)、つまりデータの[mathjax]\( x\)軸方向の平均値と[mathjax]\( y\)軸方向の平均値はあらかじめ決められているものとします。
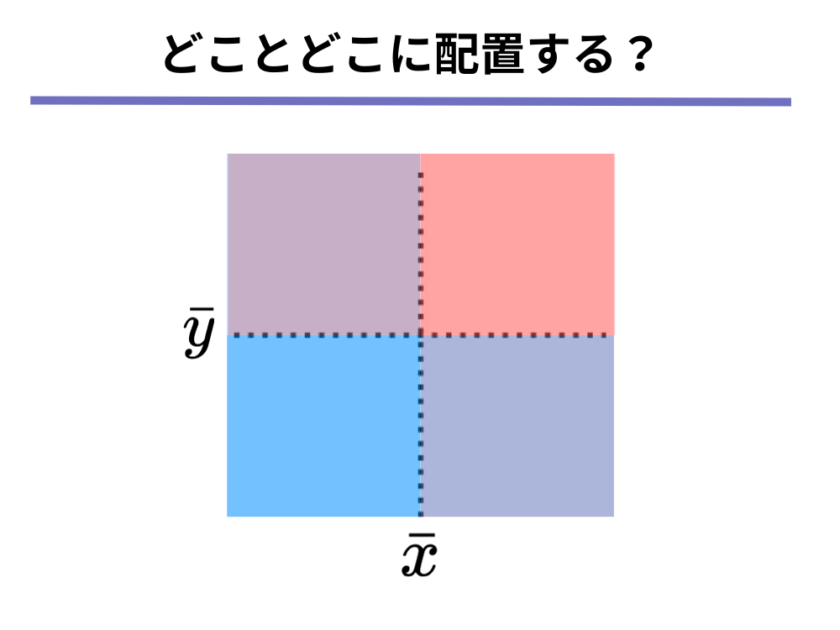
ここで思い出していただきたいのは、以下の2つの事実です。
- 赤または青のエリアに点[mathjax]\( x_i, y_i \)を配置すると、[mathjax]\( (x_i – \bar{x})(y_i – \bar{y}) \)の値はプラスになる
- 紫のエリアに点[mathjax]\( x_i, y_i \)を配置すると、[mathjax]\( (x_i – \bar{x})(y_i – \bar{y}) \)の値はマイナスになる
つまり、共分散の値が0になるためには[mathjax]\( (x_1 – \bar{x})(y_1 – \bar{y}) + (x_1 – \bar{x})(y_1 – \bar{y}) \)の値がいい感じに打ち消しあって0になるようなところに2点を配置すればいいことが分かります。
例えば以下の図のように[mathjax]\( y\)座標が同じで、[mathjax]\( x\)座標は平均[mathjax]\( \bar{x}\)と同じだけ離れているようなところに2点を配置すると共分散の値は0になります。
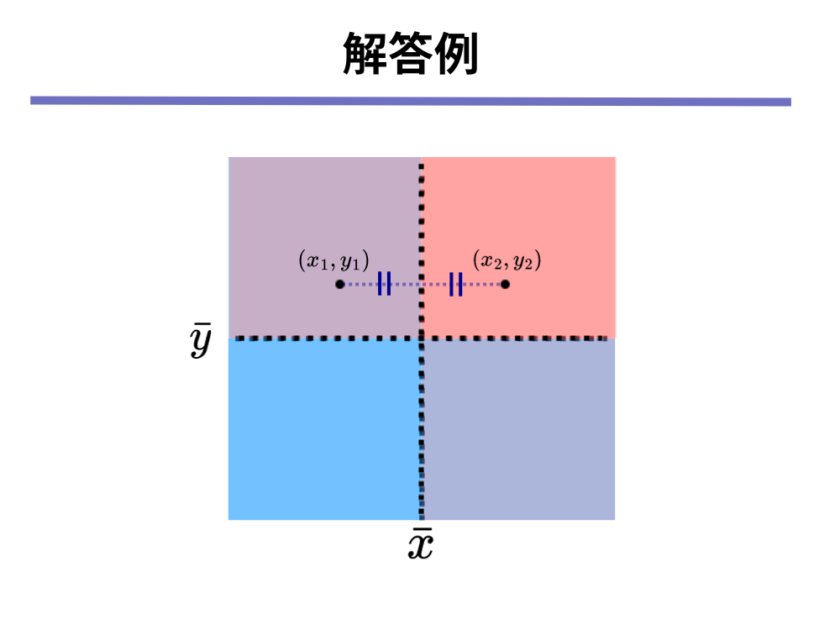
逆に[mathjax]\( x\)座標が同じで、[mathjax]\( y\)座標が平均[mathjax]\( \bar{y}\)と同じだけ離れているようなところに2点を配置しても共分散の値は0になります。
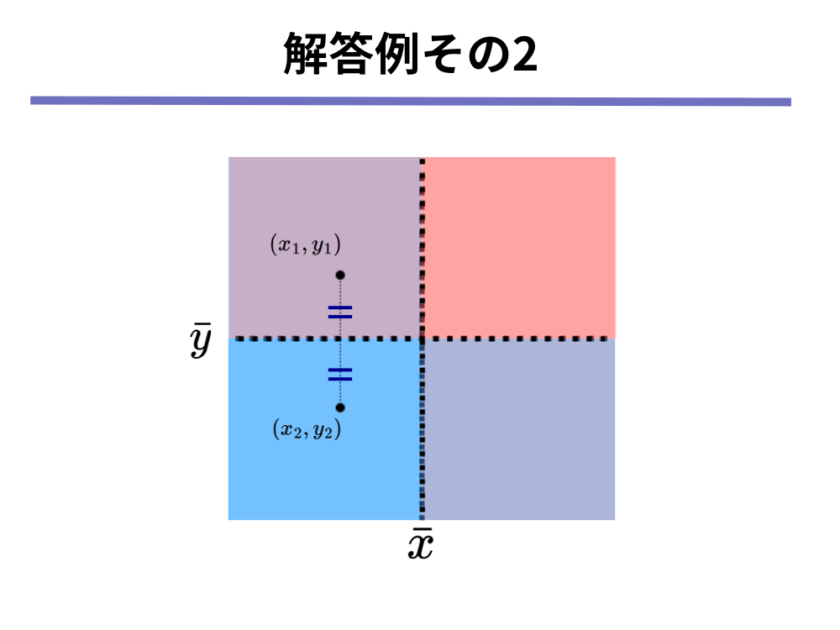
それでは、先ほどまで考えた極端な例を拡張して、どんな散布図であれば共分散が0になるのか考えて見ましょう。
まずは、[mathjax]\(y\)座標が同じで[mathjax]\(x\)座標が[mathjax]\(\bar{x}\)から同じだけ離れているような点を複数個書き足していきます。
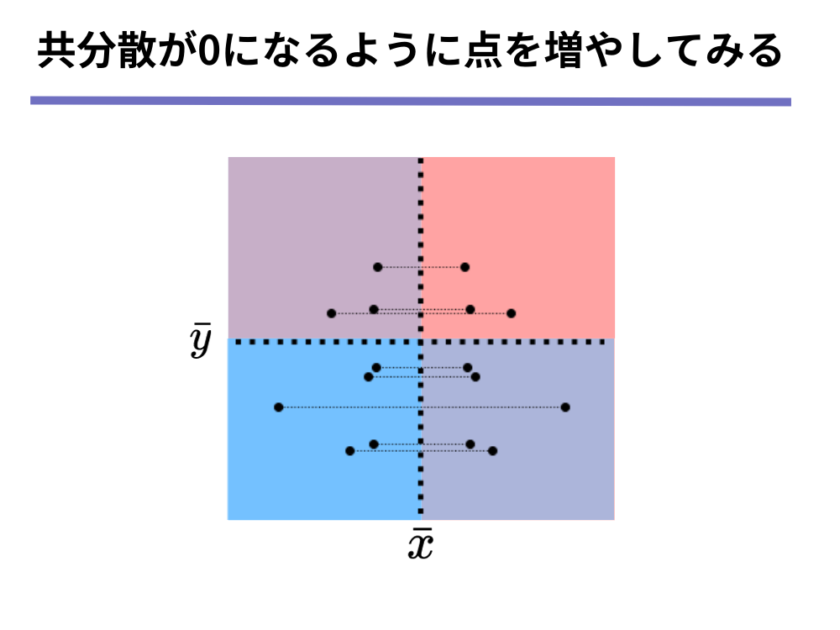
さらに[mathjax]\(x\)座標が同じで[mathjax]\(y\)座標が[mathjax]\(\bar{y}\)から同じだけ離れているような点も複数個書き足していきましょう。
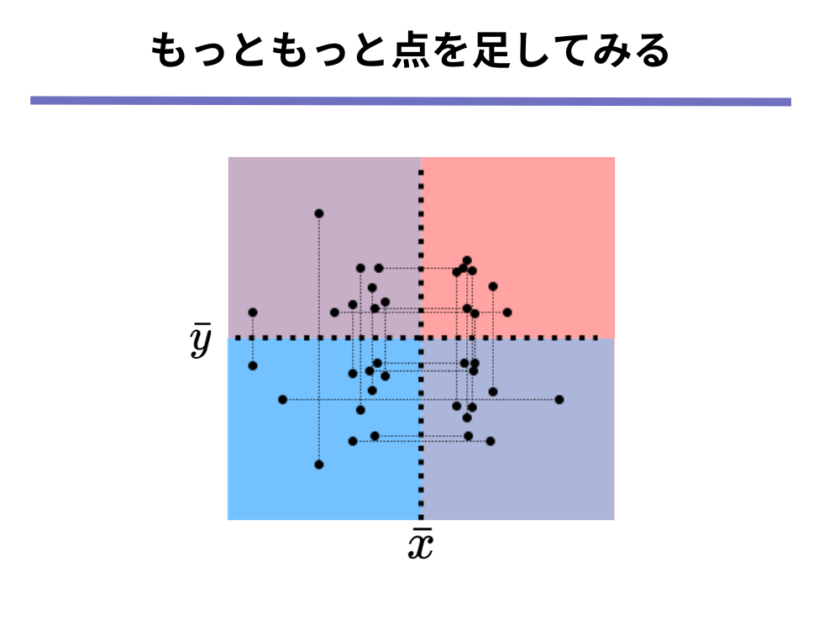
さて、以上の操作を果てしない回数繰り返していくと、以下のような散布図になります。
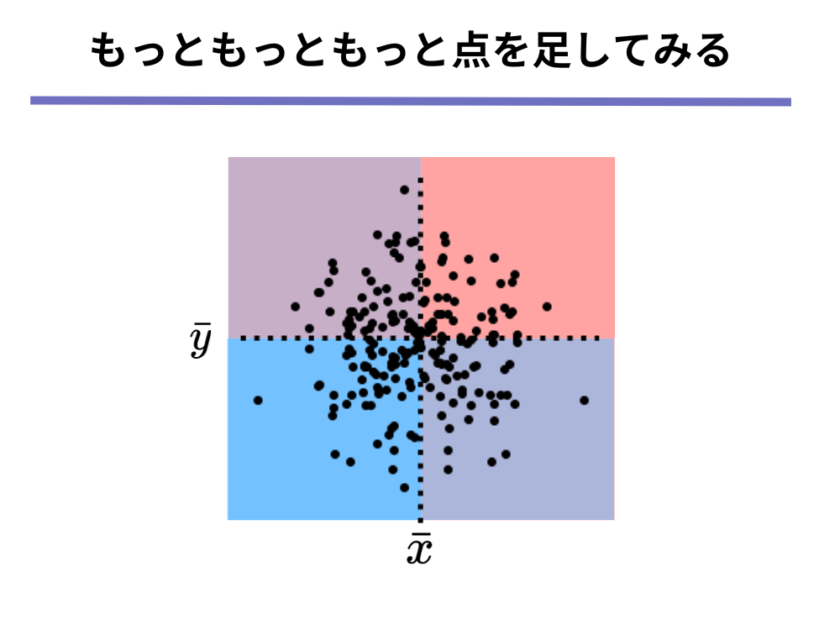
よく見ると必ずどの点も[mathjax]\( x\)軸または[mathjax]\( y\)軸をまたいで反対側に対になる点があることが分かります。
つまり上の散布図も間違いなく共分散0ということができます。
よって、共分散が0であるような散布図とは、「どのエリアにもまんべんなくデータ点があるような散布図」ということができます。
※実は上の図のような全てのエリアにまんべんなくデータ点があるような散布図以外にも共分散が0になるような散布図はあと2パターンあります。
ヒントは「すべての[mathjax]\((x_i – \bar{x} )(y_i – \bar{y} )\)が0になるとき、共分散は0である」ということ。
お時間ある時に考えてみてくださいね!
なぜ分母に標準偏差のかけ算があるのか
ここまでで共分散と相関の関係については理解いただけたかと思います。
改めて整理してみると、以下のような関係になっています。
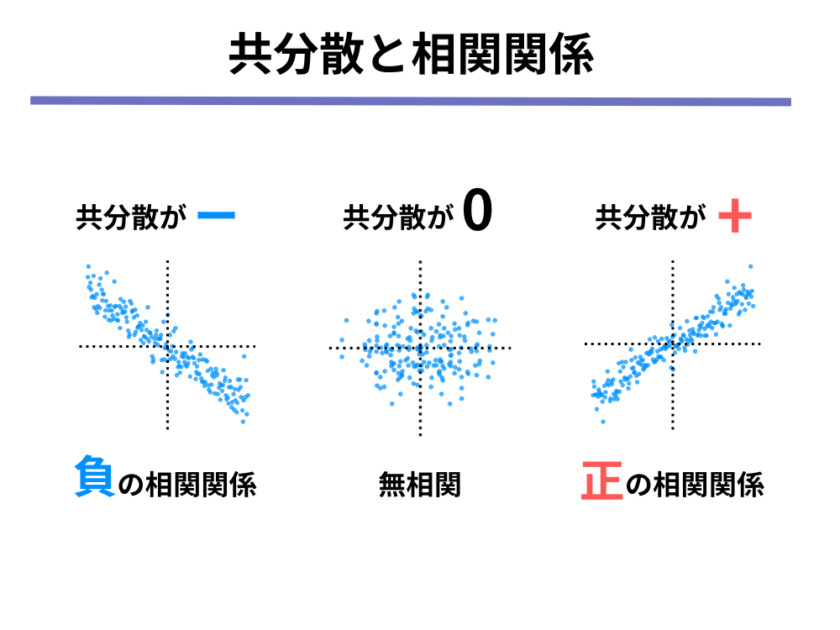
- 共分散がプラスの時 → 正の相関関係がある
- 共分散が0の時 → 相関関係がない(無相関)
- 共分散がマイナスの時 → 負の相関関係がある
さて、今度は共分散の値の大きさと相関の強さとの関係について考えていきましょう。
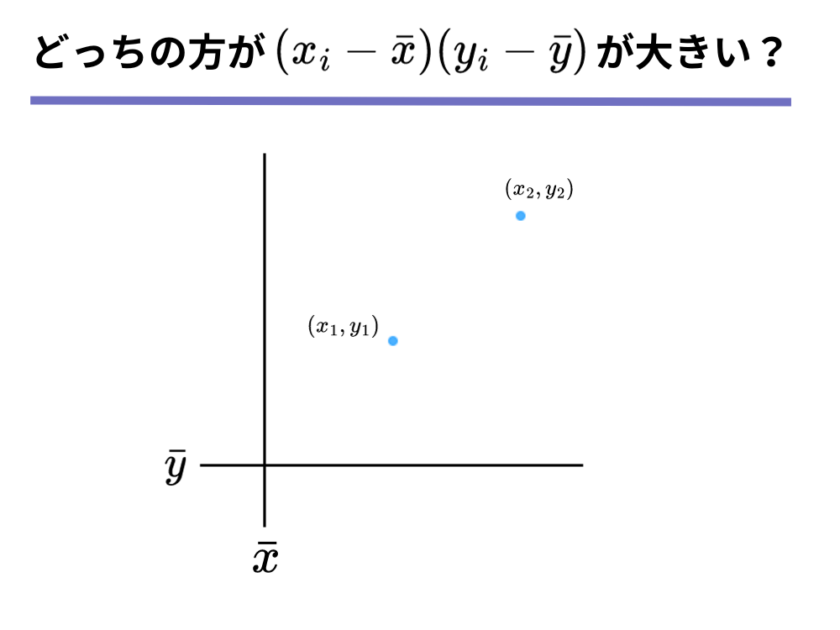
まずは皆さんと考えていきたいのは、以下のように図示した2つの点[mathjax]\((x_1, y_1)\)と[mathjax]\((x_2, y_2)\)のどちらの点の方が[mathjax]\((x_i – \bar{x})(y_i – \bar{y})\)の値が大きいでしょうか。
ただし、[mathjax]\(\bar{x}\)と[mathjax]\(\bar{y}\)はすでに決まっているものとします。
いかがでしょうか?
[mathjax]\((x_i – \bar{x})(y_i – \bar{y})\)の値が大きいのはどちらだと思いますか?
これはそれぞれの点が平均[mathjax]\(\bar{x}\)と[mathjax]\(\bar{x}\)からどれだけ離れているか考えれば分かりますね。
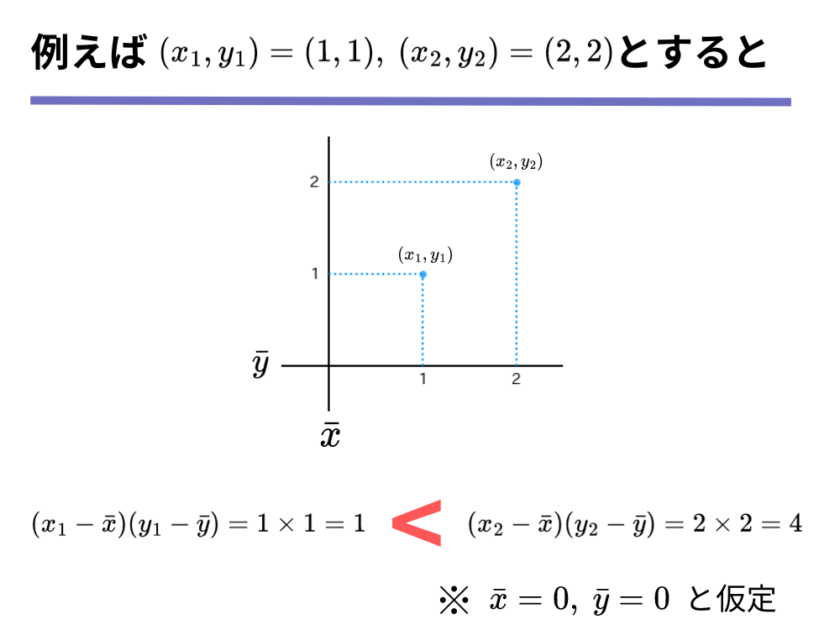
答えは点[mathjax]\((x_2, y_2)\)です!
[mathjax]\( \bar{x}\)からの距離と[mathjax]\( \bar{y}\)からの距離のかけ算の値を比較することになるので、平均から遠い点[mathjax]\((x_2, y_2)\)の方が値が大きくなりますね。
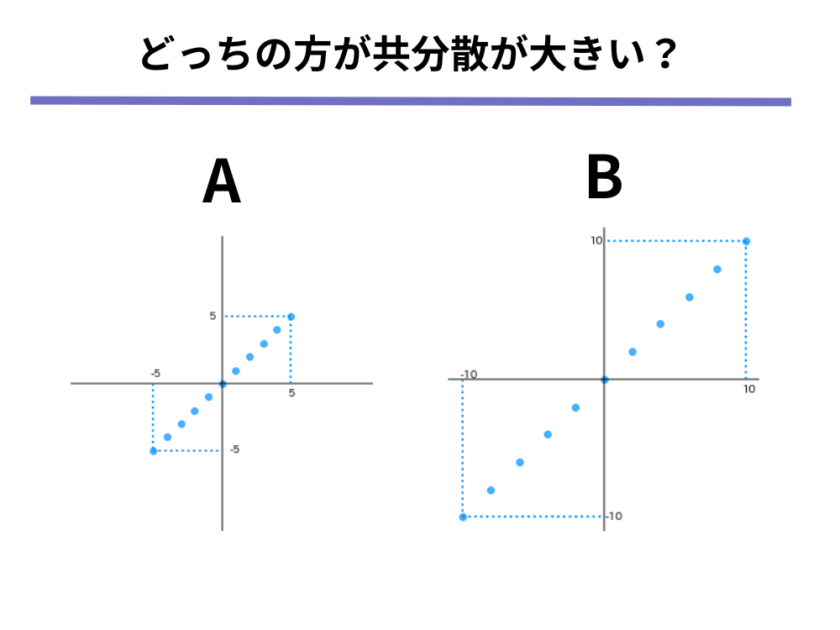
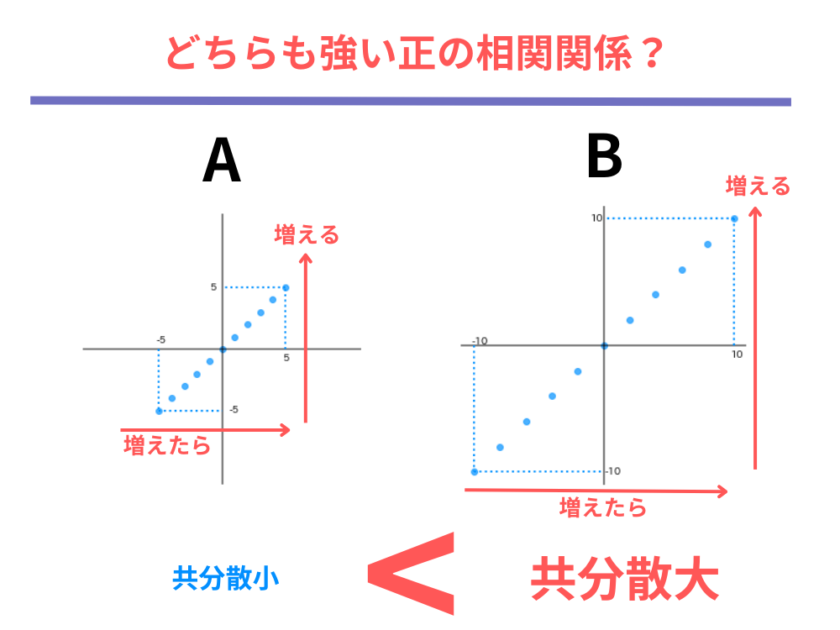
ここまでの議論を踏まえて、以下の2つの散布図のうち共分散の値が大きいのはどちらでしょうか。
いかがでしょうか?どちらが共分散が大きいか分かったでしょうか。
1つの前の図で考えると、平均から外れているほど共分散の値は大きくなることが分かりました。
それを踏まえて上の図を見てみると、左の図は端の点でも(5,5)であるのに対して、右の図では端の点は(10,10)であるように、左の図より2倍ほど離れた点があることが分かります。
よって、共分散が大きい散布図は右の図になります。
ここで、皆さんに考えていただきたいのは「共分散の大きい右の図のほうが相関が強いと言えるか」ということです。
確かに共分散の大小が相関の強弱と関連するのならば、右の散布図の方が相関が強いと言えそうですが、果たして本当にそうでしょうか。
左の図も右の図も、どちらも点は右斜め上に向かって一直線上に上がっており、正の相関が「片方が増えたらもう片方も増える」という傾向があることであったことを踏まえると、どちらも「強い正の相関」と言えるのではないでしょうか。
一方で共分散の値は相関係数が強いのか弱いのか、正の相関なのか負の相関なのかを表す重要な指標であることはここまで学んできた通りです。
それでは、どうやってこの矛盾、「相関関係を見る上では共分散が重要」「共分散の大小だけでは相関係数の強弱は測れない」を解決するのでしょうか。
そこで重要になってくるのが、やっとお出まし、相関係数の定義式の分母にいらっしゃいました「[mathjax]\( x\)の標準偏差」と「[mathjax]\( y\)の標準偏差」です。
標準偏差とはデータがどれだけ平均から離れているかを表すばらつき具合の指標です。
詳しい解説は以下の記事に載っていますので、気になる方はご覧ください!
標準偏差が相関係数の定義式で果たす役割
さて、ここで再度相関係数の定義式を提示しておきましょう。

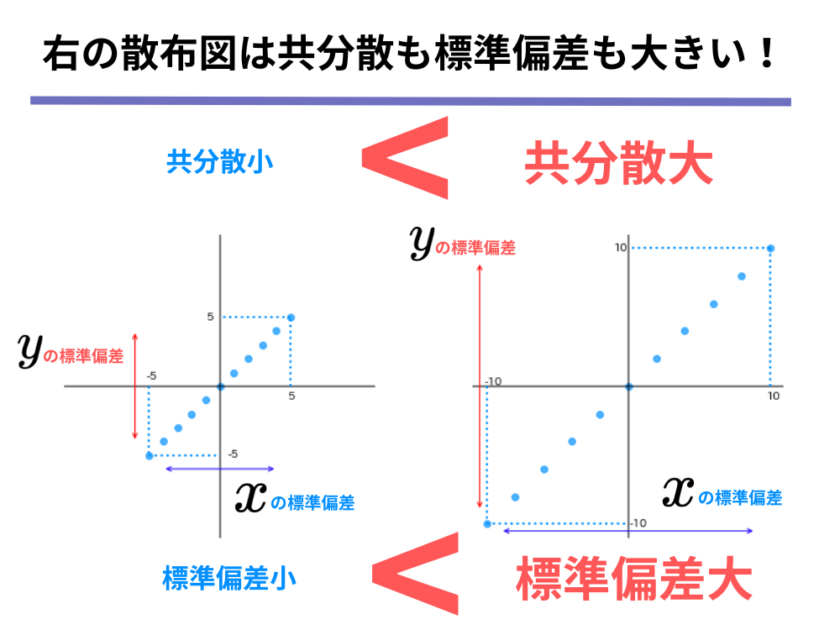
さて、先ほどの左右の散布図では、「両方とも強い相関関係にありそうなのに、右の散布図の方が共分散の値が大きい」というのが相関の強さを考える上での問題になっていました。
ここで、上の相関係数の定義式の散布図を見てもらうと、が左右のばらつきを[mathjax]\( x\)の標準偏差が、上下のばらつきを[mathjax]\( y\)の標準偏差が表現していることが分かります。
そして思い出して欲しいのは、先ほどの左右の散布図では、「右の散布図は共分散の値が大きいが、[mathjax]\( x\)の標準偏差と[mathjax]\( y\)の標準偏差の値も大きい(=左右上下のばらつきも大きい)」ということです。
さて、それでは上記の話について具体的な例を用いて考えていきましょう。
ある学校Aでは先月10人の生徒が風邪を引きました。
もう一方の学校Bでは先月100人の生徒が風邪を引きました。
どちらの学校の方が風邪をひきやすいでしょう?
この問題は簡単ですね、学校Bの方が学校Aよりも10倍の人が風邪を引いているので、答えはBですね!
…としてはいけないのが、ここまでの議論でお分かりでしょうか。
実はこの問題には大事な部分が抜けています。
それは、「学校全体の生徒数」という視点です。
それでは、学校全体の生徒数について、追加の情報を与えましょう。
学校Aは自然豊かな郊外の学校で、全校生徒は100人です。
学校Bは都市部の学校で、全校生徒は1000人です。
改めて、どちらの学校の方が風邪を引きやすいでしょうか。
ここで、それぞれの学校の生徒がどれぐらいの割合で風邪を引いているのか計算してみましょう。
学校Aの風邪の人の割合は[mathjax]\( 10 \div 100 = 0.1 \)なので、10%の人が風邪を引いています。
学校Bも同様に[mathjax]\( 100 \div1000 = 0.1\)なので、10%の人が風邪を引いています。
よって、どちらの学校も全校生徒の10%が風邪を引いていることから、風邪の引きやすさは同程度と言えることが分かります。
以上の風邪の例を図にまとめると以下のようになります。
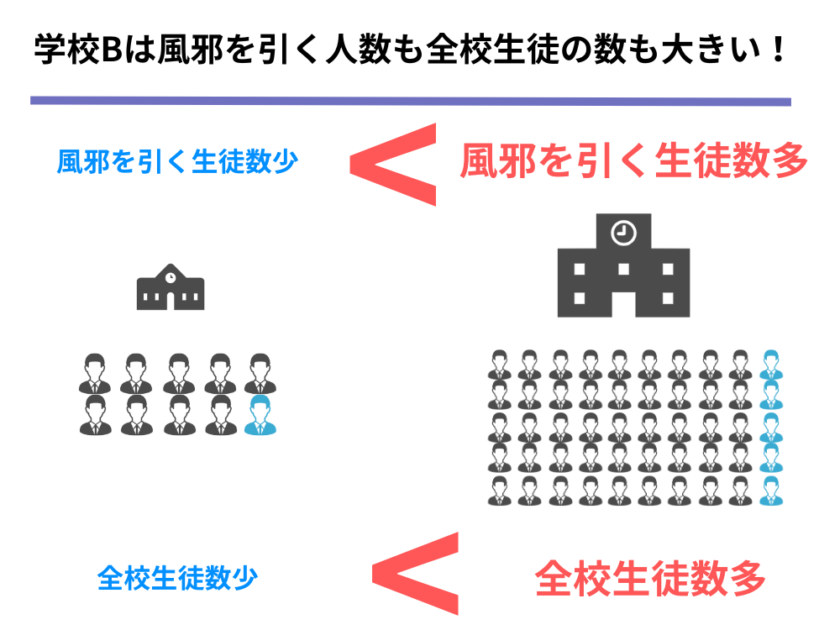
そして、上の図を見ると、共分散と標準偏差の関係と、風邪の生徒数と全校生徒数の関係が同じような関係になっていることが分かります。
風邪の生徒の話では「全体に何人生徒がいて、その中の何人が風邪を引いているのか」で考えることが重要でした。
共分散についても同じことがいえ、「全体ではどれだけバラついていて(=標準偏差)、その中で共分散の値がどれだけプラスまたはマイナスなのか」で考えることが重要なのです。
そして、風邪の生徒の例では「風邪の生徒数を全校生徒数でわり算して、風邪の人の割合」を求めました。
共分散の場合も同様に「共分散の値を縦横両方の方向のばらつきの度合い(=[mathax]\(x\)と[mathax]\(y\)の標準偏差のかけ算)でわり算して、相関の度合い」を求める、ということが【相関係数】の意味するところです。
相関係数に関する統計検定3級類似問題
それでは、実際に統計検定3級で出題された問題の類似問題を解きながら、相関係数について理解を深めていきましょう!
次の散布図は、2022年のJリーグにおける各チームの得失点差(得点[mathjax]\(-\)失点)と勝利数を表したものです。
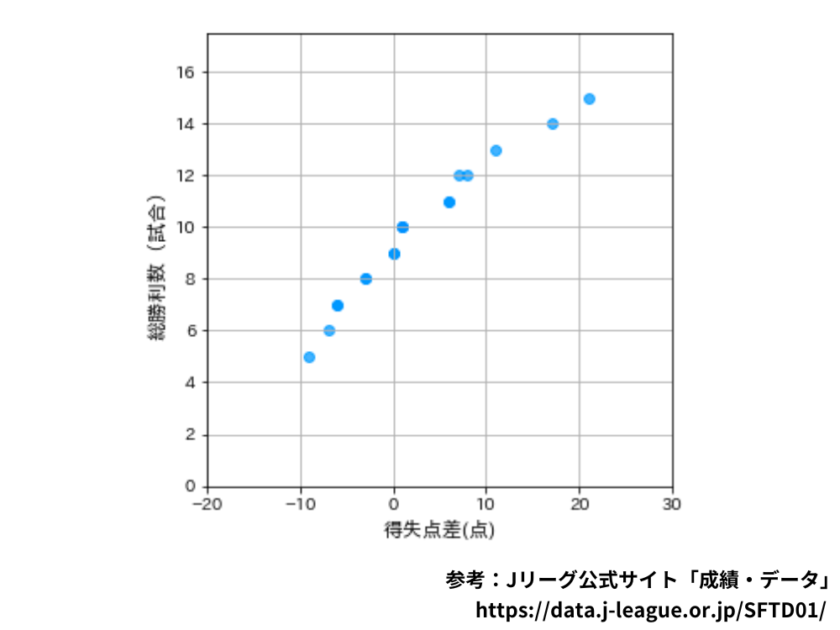
この散布図から読み取れることとして、次の①〜③の記述を考えました。
①得失点差がプラスのチームは、得失点差がマイナスのチームに比べて勝利数が多い傾向がある。
②得失点差がマイナスのチームは、得失点差がプラスのチームに比べて勝利数が多い傾向にある。
③得失点差と勝利数には強い負の相関があり、得失点差が最も小さいチームは、勝利数が最も少ない。
上記の記述①〜③に関して、正誤を判定してください。
この問題は「正の相関、負の相関とはどういう散布図で表されるか」を覚えていれば簡単に解けることでしょう。
それでは、解説に参りましょう!
①と②については同時に考えてみましょう。
散布図の横軸は得失点差を表していることから、右側に行けば行くほど得失点差がプラスに大きいチーム、つまり得点の方が失点よりも多いチームであり、左側に行けば行くほど得失点差がマイナスに大きい、つまり失点の方が得点よりも多いチームであることが分かります。
一方で、縦軸は総勝利数を表しているため、上に行けば行くほど勝利数の多いチーム、下に行けば行くほど勝利数の少ないチームであることが分かります。
そして①の「得失点差がプラスのチーム」というのは散布図の右側にあるチームであり、それらのチームは他のチームに比べて総勝利数が多いことが分かります。
一方で②の「得失点差がマイナスのチーム」というのは散布図の左側にあるチームであり、それらのチームは他のチームに比べて総勝利数が少ないことが分かります。
よって、①については正であり、②については誤であることが分かります。
続いて、③については「得失点差と総勝利数はどのような相関関係にあるか」について考えれば自ずと答えは導かれます。
散布図を見ると「得失点差が増えると、総勝利数も増える」という関係にあることが分かります。
このような関係にある散布図のことを「正の相関関係にある」というでしたね。
よって、③の文章は「強い負の相関」と真逆のことを指し示しているので、誤であることが分かります。
Python/Rでの散布図の描き方とPython/R/SQLでの相関係数の計算方法
先ほどはJリーグの各チームの試合データを使用して得失点差と総勝利数の相関関係について理解を深めましたが、今度はPython/Rを使って得失点差と総勝利数に関する散布図を描きましょう!
また、Python/R/SQLを使って、得失点差と総勝利数の相関係数を計算してみましょう!
次のj_league_data.csvは2023年のJリーグの試合データが入力されています。
(1) 得失点差と総勝利数の散布図を作成してください
(2) 得失点差と総勝利数の相関係数を計算してください
(1) まずはcsvを読み込み、データの中身を見てみましょう。
#csvを読み込むためにpandasをインポート
import pandas
#csv読み込み
df = pd.read_csv('j_league_data.csv')
#データの中身を表示
display(df)データの中身を表示してみると、このデータには「得失点差」という列(カラム)はなく、得点列と失点列があるのみです。
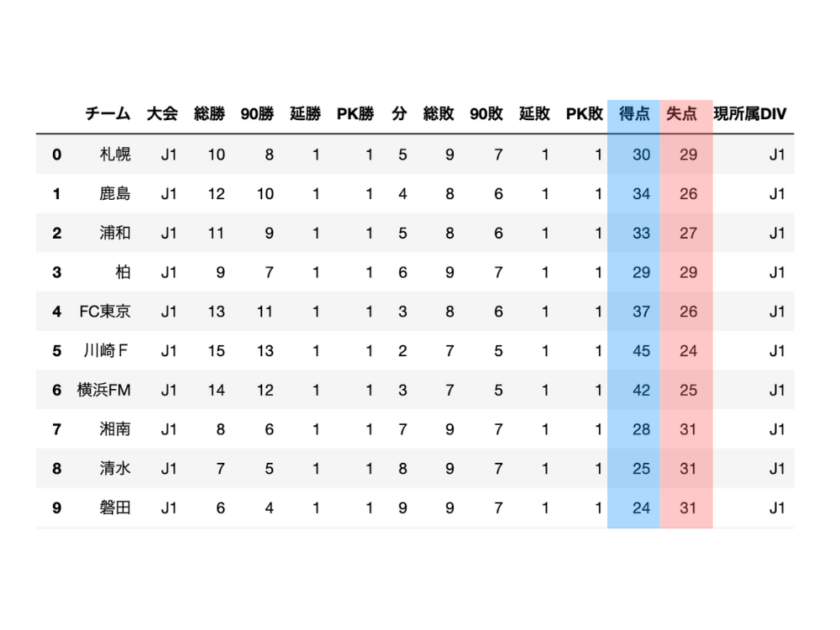
なので、まずは得点列と失点列から得失点列を作成しましょう。
#得点と失点から得失点差を計算
df['得失点差'] = df['得点'] - df['失点']
#再度データの中身を出力
display(df)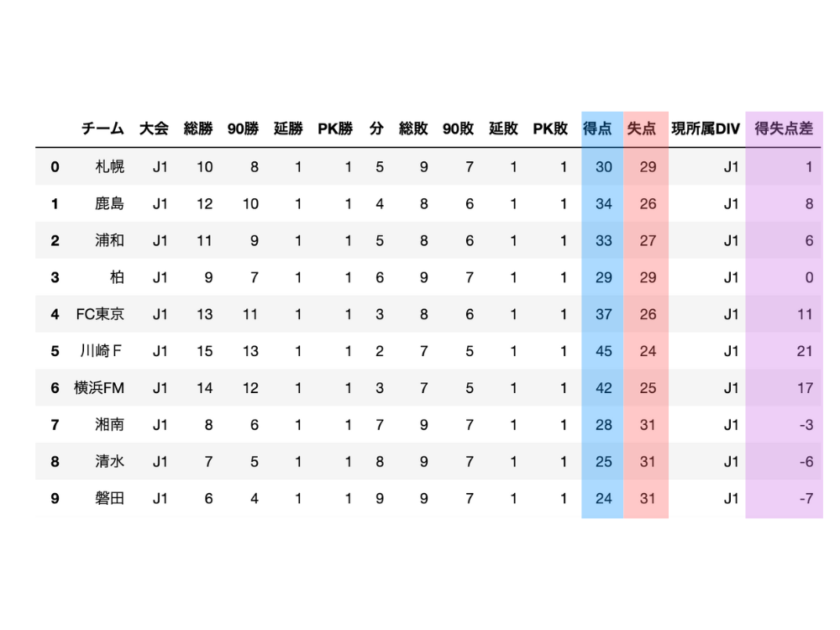
これで、散布図作成のための準備は完了です。
次に、Pythonにおける可視化用のライブラリ「matplotlib」やmatplotlibで日本語を出力するためのライブラリ「japanize-matplot」をインポートしてから、散布図を可視化してあげれば完成です。
#可視化をするためにmatplotlibをインポート
import matplotlib.pyplot as plt
#matplotlibで日本語を出力するためにjapanize_matplotlibをインポート
import japanize_matplotlib
#横軸が得失点差、縦軸が総勝になるように点を出力
plt.scatter(df['得失点差'], df['総勝'])
#横軸と縦軸にラベル付けを行う
plt.xlabel('得失点差(点)', fontsize = 12)
plt.ylabel('総勝利数(試合)', fontsize = 12)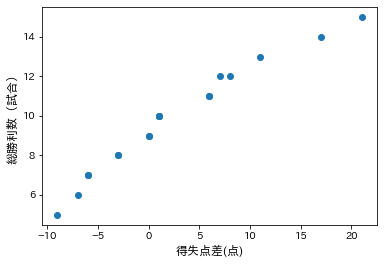
(2) PythonではPandasライブラリのcorr()関数を使用すれば、テーブル内の様々な列同士の相関係数を可視化することができます。
ただし、文字列が入っている列や全て同じ数字が入っていると適切に相関係数を計算できないので、それらの行はあらかじめ取り除いておきます。
「全く同じ数字が入っていると適切に相関係数を計算できない」のはなぜなのかについては、相関定数の定義式を振り返りながら考えてみましょう!
# 相関係数のヒートマップの可視化に必要なライブラリseabornをインポート
import seaborn as sns
# 不要な列をデータから削除
tmp = df.drop(['チーム', '大会', '現所属DIV', '延勝' , 'PK勝', '延敗', 'PK敗'], axis = 1)
# corr()関数を使用して相関係数を計算
cor = tmp.corr()
# 相関係数の計算結果をヒートマップで可視化
sns.heatmap(cor, cmap = sns.color_palette('coolwarm', 10), annot = True, fmt = '.2f', vmin = -1, vmax = 1)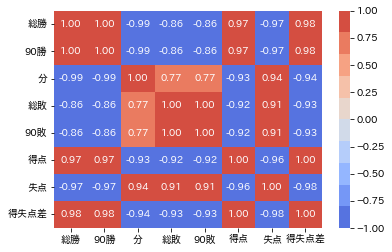
このように可視化をしてみると、求めるべき答え「得失点差と総勝の相関係数」は一番右上の数字、つまり0.98であることが分かります。
相関は英語でCorrelationと訳すので、相関係数を計算する関数ではcorrがよく使われます
(1) Pythonの場合と同様に、得失点差列を作成してから散布図を作成していきます。
# csv読み込み
df <- read.csv('j_league_data.csv')
# 得失点差列の作成
df$得失点差 <- df$得点 - df$失点
# 日本語が文字化けしないように調整
par(family = 'HiraKakuProN-W3')
# 散布図の出力
plot(df$得失点差, df$総勝)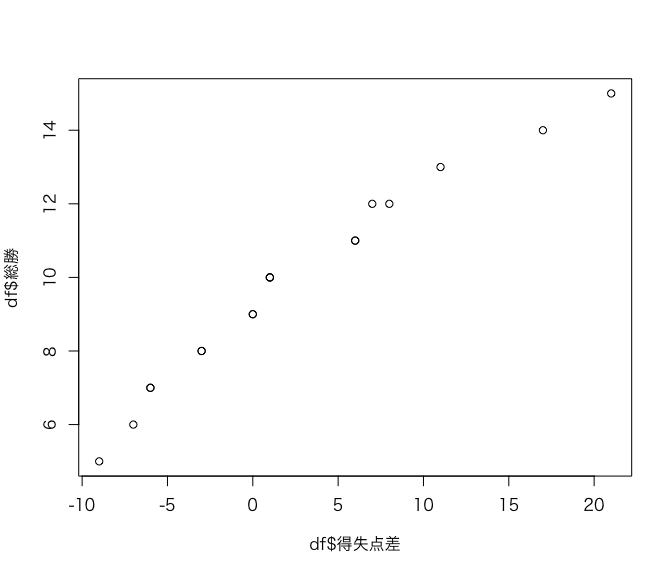
(2) Pythonの解法と同様に、文字列を含む列、全て同じ数字の列を削除した上で相関係数を計算します。
Rでは、drop()の代わりにsubsetを、seabornライブラリの代わりにcorrplotライブラリを、heatmap()の代わりにcorrplot()を使用します。
# 相関係数の可視化に必要なライブラリをインポート
install.packages('corrplot')
install.packages('dplyr')
library(corrplot)
library(dplyr)
# 不要な列をデータから削除
tmp <- subset(df, select = -c(チーム, 大会, 現所属DIV, 延勝 , PK勝, 延敗, PK敗))
# 相関係数を計算(計算方法にはピアソンの積率相関を使用)
corr <- cor(tmp, method = 'pearson')
# 相関係数を可視化
corrplot(corr, tl.col = 'black', method = 'number')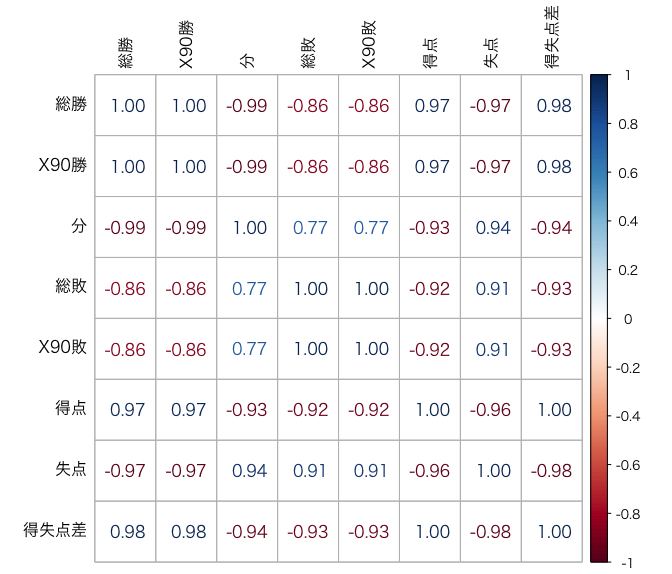
次のSQL文を実行して、j_league_dataテーブルを定義し、得失点差と総勝利数の相関係数を計算してください。
CREATE TABLE JLeague
(
win INTEGER,
win_lose_diff INTEGER
);
INSERT INTO JLeague VALUES(10, 1);
INSERT INTO JLeague VALUES(12, 8);
INSERT INTO JLeague VALUES(11, 6);
INSERT INTO JLeague VALUES(9, 0);
INSERT INTO JLeague VALUES(13, 11);
INSERT INTO JLeague VALUES(15, 21);
INSERT INTO JLeague VALUES(14, 17);
INSERT INTO JLeague VALUES(8, -3);
INSERT INTO JLeague VALUES(7, -6);
INSERT INTO JLeague VALUES(6, -7);
INSERT INTO JLeague VALUES(10, 1);
INSERT INTO JLeague VALUES(9, 0);
INSERT INTO JLeague VALUES(12, 7);
INSERT INTO JLeague VALUES(11, 6);
INSERT INTO JLeague VALUES(10, 1);
INSERT INTO JLeague VALUES(8, -3);
INSERT INTO JLeague VALUES(7, -6);
INSERT INTO JLeague VALUES(5, -9);PostgreSQLではcorr()関数を使えば、2つの列同士の相関係数を計算することができます。
SELECT
corr(win, win_lose_diff) as 相関係数
FROM
JLeague
まとめ
この記事では統計学の基礎である相関について、定義から定義の意味するもの、実践例まで見てきました!
「バズる広告は本当に売上に影響を及ぼすのか」「価格を下げれば売り上げが上がるのか」など、2つのデータの関係性を検証する時に相関係数は威力を発揮します!
一方で、相関関係を分析するときは「相関関係があるからといって、因果関係があるとは限らない」(=アイスクリームの売上と水死者数には相関関係はあるが因果関係はない)という非常に重要な視点を持つ必要があるので、詳しい解説については今後記事でしていこうと思います!
今日も勉強おつかれさまでした!



コメント