統計学の青本「自然科学の統計学」の2×4分割表におけるカイ二乗適合度検定の問題をPythonを使って解いてみた

今回の記事では、統計学の青本「自然科学の統計学」の第5章「適合度検定」の演習問題3「2$\times$4分割表の検定」における「作業員によって不良率に差異がある」という仮説に対する$chi^2$適合度検定のPythonでの実装について紹介いたします！

今回の場合はシンプルなカイ二乗検定の実装になっているので、カイ二乗検定の最もオーソドックスなパターンについて理解を深めたい方はご参考にしていただけると幸いです！

問題文
実装コード
実装コード解説
まとめ

問題文

＜2$\times$4分割表の検定＞

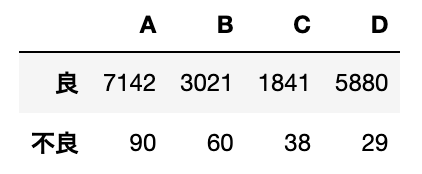
ドラム缶の巻締不良を4人の作業員別に集計して、次の結果を得た。

$\chi^2$適合度検定を用い、作業員によって不良率に差異がないという仮説を有意水準5%で検定せよ

東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章　適合度検定 P174~175

今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。

実装コード

今回の問題を解くに際して、Pythonで実装したコードは以下の通りです。

import numpy as np
import pandas as pd
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2

df = pd.read_csv('Failure to wind and tighten drums.csv', index_col = 0)
cols = df.columns 
indices = df.index

# 全てのセルの合計を計算
n = df.sum().sum()

# カイ二乗値を計算
chi_square = 0

for col in cols:
    for index in indices:
        # 行の合計を計算
        index_sum = df.loc[index, :].sum()
        # 列の合計を計算
        col_sum = df.loc[:, col].sum()
        # セルの値を抽出
        cell = df.loc[index, col]
        # 各セルにおけるカイ二乗値を計算
        chi_square += ( n * cell - col_sum * index_sum) ** 2 / (n * col_sum * index_sum)
        
txt = r"$\chi^2 = $" + str(chi_square)

# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()

#  自由度  = 列の自由度 * 行の自由度
v = (len(indices) - 1) * (len(cols) -1)
print(f'自由度: {v}')
alpha = 0.05

chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")

if chi_square > chi2_pdf:
    print('「不良品に差がない」という仮説は有意水準5%で適合しない')
else:
    print('「不良品に差がない」という仮説は有意水準5%で適合する')

実装コード解説

今回の問題は以下の4ステップによって解くことができます。

全体の合計値を算出する
行の合計、列の合計、各セルの値を利用して、セルごとの$\chi^2$値を合算する
自由度を算出する
自由度と有意水準から算出された$\chi^2$分布の値とデータから算出された$\chi^2$値を比較し、検定を完了する

順を追って解説をしていきます。

全体の合計値を算出する

# 全てのセルの合計を計算
n = df.sum().sum()

上記計算によって算出された全体の合計値は「作業員ごとの不良率に差異はない」という前提に立った場合の理論値を計算する際に使用します

行の合計、列の合計、各セルの値を利用して、セルごとの$\chi^2$値を合算する

$\chi^2$値は以下の式によって計算することができます。

$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$

ここで、今回の問題における期待度数ですが、「作業員の不良率に差異はない」という仮説に立脚すると、以下のような式で表現することができます。

$$ 期待度数_{ij} = \frac{(i行の合計f_{i\cdot} \times j列の合計f_{\cdot j})}{全体の合計数n}$$

例えば「親の収入と子の収入には相関がない」という仮説における、以下のような表を考えてみましょう。

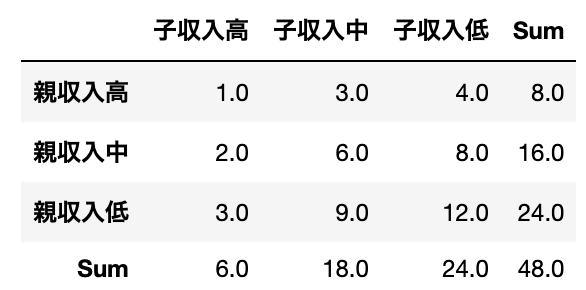
上記の表においては、Sum以外の全てのセルで以下の関係が成り立っています。

$$ (各セルの値) = \frac{(行の合計) \times (列の合計)}{全てのセルの合計48}$$

（例: $(親の収入高, 子の収入高のセル) = \frac{8\times 6}{48} = 1$）

このような状況では以下のような2つの関係が成り立っています

行方向に数字を見ると、1:3:4の関係が成り立っている
列方向に数字を見ると、1:2:3の関係が成り立っている

つまり、親の収入に関係なく子の収入は1:3:4の比率で存在するので、親の収入と子の収入は関係ないということがわかります。

「仮説が正しいなら、この値になるはずだよね？？」という期待を込めて期待度数と呼んでいるのです。

一方で、「期待通りでない」パターンをみてみましょう。

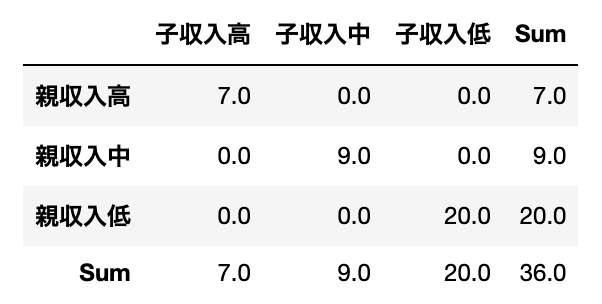
この表を見ると、親の収入が高いほど子の収入が高く、親の収入が低いほど子の収入も低いという関係が一目瞭然です。

そして、この表に対して先ほどと同様の式で期待度数を計算すると、以下の表のようになります。

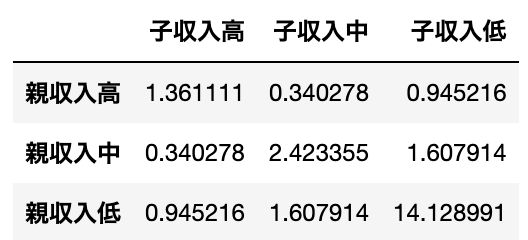
1つ前の表と見比べると各セルの値、特に対角線の値が大きくずれていることがわかります。

なぜこんなに値がずれてしまっているかというと、期待度数を計算する際に使った「親の収入と子の収入には相関がない」という前提が間違っているためです。

このようにして、実際の値と期待度数の値の差の値を検証することによって、仮説が正しいか判定するのが$\chi^2$適合度検定であり、その計算を行う式が先ほど紹介した以下の式になるのです。

$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$

よって、上記の式を実現する実装コードは以下のようになります。

# カイ二乗値を計算
chi_square = 0

for col in cols:
    for index in indices:
        # 行の合計を計算
        index_sum = df.loc[index, :].sum()
        # 列の合計を計算
        col_sum = df.loc[:, col].sum()
        # セルの値を抽出
        cell = df.loc[index, col]
        # 各セルにおけるカイ二乗値を計算
        chi_square += ( n * cell - col_sum * index_sum) ** 2 / (n * col_sum * index_sum)
        
txt = r"$\chi^2 = $" + str(chi_square)

# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()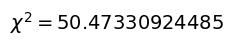

自由度を算出する

ここまでで、実際のデータにおける$\chi^2$値を計算することができました。

最後に、理論上の$\chi^2$値を計算するために、今回のデータの自由度を計算します。

#  自由度  = 列の自由度 * 行の自由度
v = (len(indices) - 1) * (len(cols) -1)
print(f'自由度: {v}')

自由度と有意水準から算出された$\chi^2$分布の値とデータから算出された$\chi^2$値を比較し、検定を完了する

最後に、自由度と有意水準5%を使って、理論上の$\chi^2$値を計算し、実際のデータから得られた$\chi^2$値と比較して、$\chi^2$適合度検定の結論を出します。

なお、先ほどの収入に関する表で見たように、理論上の$\chi^2$値よりも差が小さい（最も理想は0）場合は「仮説は正しい」（=仮説に適合する）とし、理論上の$\chi^2$値よりも差が大きい場合は「仮説は正しくない」（=仮説に適合しない）と結論づけます。

alpha = 0.05

chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")

if chi_square > chi2_pdf:
    print('「不良品に差がない」という仮説はは有意水準5%で適合しない')
else:
    print('「不良品に差がない」という仮説は有意水準5%で適合する')