
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第6章-演習問題4「二項確率の検定の標本の大きさ」にPythonを適用して問題を解いていきたいと思います。
今回の記事を読めば、検定したい確率$p_0$と確率$p$の時の検出力$\gamma$が定まれば必要なサンプルサイズが決定できることを学ぶことができます!
要は求められる水準になるような検定に必要なサンプルサイズを求めることができるので、ぜひ参考にしてみて下さい!
問題文
<二項確率の検定の標本の大きさ>
2項分布の成功確率の片側検定で、$p_0=0.4$とし、$p=0.6$の時の検出力を0.9以上にしたい。このために必要な標本の大きさを求めよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第6章 演習問題 P200
実装コード
今回の問題を解くためのコードは以下のとおりです。
import numpy as np
from scipy.stats import norm
# 初期設定
p0 = 0.4
p = 0.6
gamma = 0.9
alpha = 0.05
# 各パーセントポイントにおける上側確率を求める
z_alpha = norm.ppf(1 - alpha)
z_gamma = norm.ppf(1- gamma)
# サンプルサイズを求める
n = (z_alpha * np.sqrt(p0 * (1- p0)) - z_gamma * np.sqrt(p * (1-p)))**2 / (p - p0)**2
print(f"サンプルサイズは{n: .2f}以上の整数")解説
今回の問題は、以下の2ステップで解くことができます。
- 有意水準$\alpha$と必要な検出力$\gamma$に対応する上側確率$z_{\alpha},~z_{\gamma}$を求める
- $z_{\alpha},~z_{\gamma},~p,~p_0$を使って、サンプルサイズ$n$の下限を求める
順を追って解説していきます。
有意水準$\alpha$と必要な検出力$\gamma$に対応する上側確率$z_{\alpha},~z_{\gamma}$を求める
有意水準$\alpha$と検出力$\gamma$に対応する上側確率を求めていきます。
標準正規分布の上側確率はscipy.stats.norm.ppfを使用して求めることができます。
# 各パーセントポイントにおける上側確率を求める
z_alpha = norm.ppf(1 - alpha)
z_gamma = norm.ppf(1- gamma)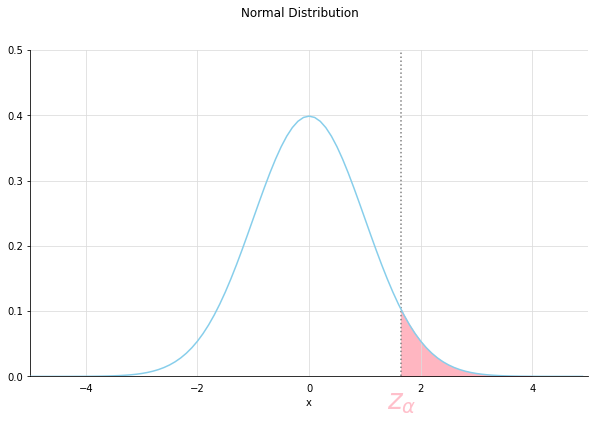
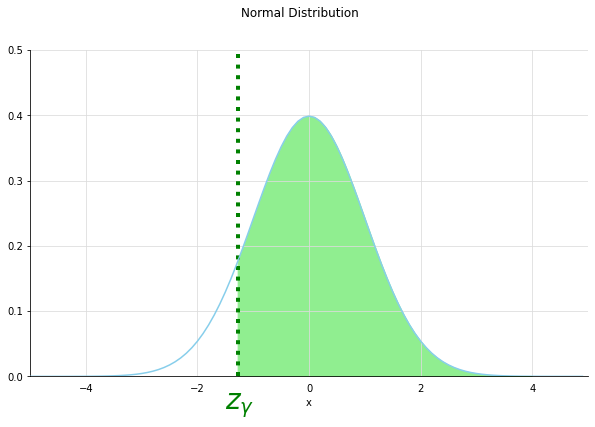
$z_{\alpha},~z_{\gamma},~p,~p_0$を使って、サンプルサイズ$n$の下限を求める
二項分布の成功確率$p$に対する片側検定において、$p>p_0$となる対立仮説の点で、$\gamma$以上の検出力を確保したい時、必要な標本サイズの下限は以下の式で求めることができます。
$$ n \geqq \frac{(z_{\alpha}\sqrt{p_0(1-p_0)} – z_{\gamma}\sqrt{p(1-p)})^2}{(p-p_0)^2}$$
# サンプルサイズを求める
n = (z_alpha * np.sqrt(p0 * (1- p0)) - z_gamma * np.sqrt(p * (1-p)))**2 / (p - p0)**2
print(f"サンプルサイズは{n: .2f}以上の整数")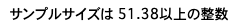
上記コードの実行結果から、必要な標本サイズは$n=52$とわかります。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第6章-演習問題4「二項確率の検定の標本の大きさ」にPythonを適用した解法を紹介いたしました。
今回は二項分布の場合のサンプルサイズを算出しましたが、検出力$\beta_{\sigma}(\theta)$の式を使えば、どのような分布に対しても必要な検出力$\gamma$を出すために必要なサンプルサイズを求めることができます。
皆さんもぜひ検出力からサンプルサイズを求め、実験前に正しいサンプルサイズを設定してみてください!



コメント