
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題1,2「ベイズの定理による確率の更新・予測分布」を丁寧めに解説してみた記事になります。
ベイズ統計学の最も基礎的な部分の話になりますので、本問題と解説でベイズに対する理解を深めていただけると幸いです!
問題文
<ベイズの定理による確率の更新>
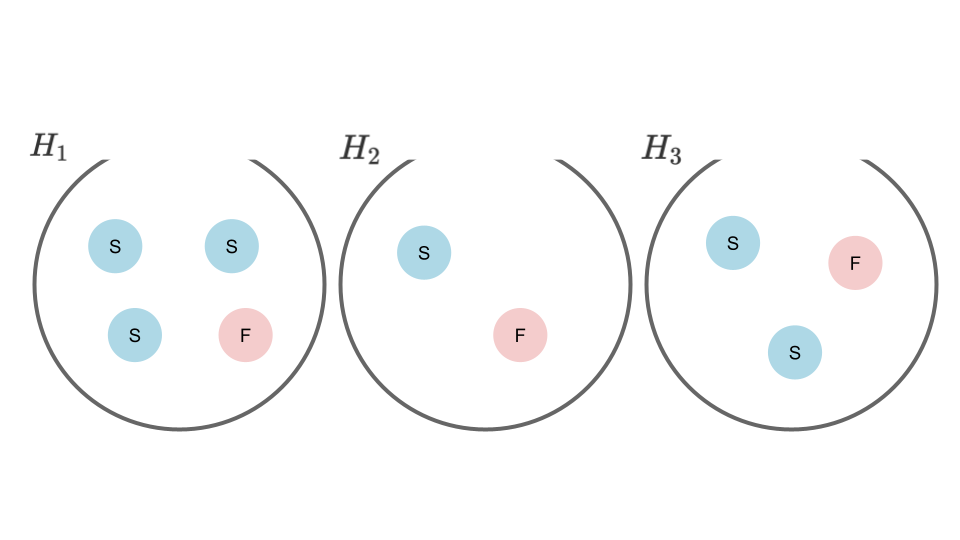
3つのつぼ$H_1,~H_2,~H_3$があり、それぞれ、$3:1,~1:1,~2:1$の比率で、$S,~F$と記された玉が入っている。ランダムに指定された壺から、玉を復元抽出で抜いた時、玉は$S$であった。
i ) その玉がつぼ$H_i(i=1,2,3)$からのものである事後確率$P(H_i|S)$は、それぞれいくつになるか。事前確率は$P(H_1) = P(H_2) = P(H_3)=1/3$とする。
ii ) 指定された同じ壺から、もう1回玉を抜いた時、再び$S$であった。回を一般に添字${}_{1,2}$で表して、これを$S_2$と表そう。この時点でのつぼ$H_i$の事後確率$P(H_i | S_1S_2)$を求めよ。
iii ) 各$H_i$に対し、$S_1S_2$の確率を考える方法で、ii) を求めよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第9章 演習問題 P273
<予測分布>
上記問題のi )と同一の状況において、次に$S$(つまり$S_2$)となる確率$P(S)$を、$P(S|H_i)(i = 1,2,3)$の期待値として求めよ。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第9章 演習問題 P273
ベイズの定理
各原因$H_1,\cdots,H_k$から事象$A$が生じる条件付き確率を$P(A|H_1),\cdots,P(A|H_k)$とする。
反対に、事象$A$が観測された時に、その原因がそれぞれ$H_1,\cdots,H_k$である確率は
$$P(H_i|A) = \frac{P(H_i)\cdot P(A|H_i)}{\sum P(H_i)\cdot P(A|H_i)$$
で計算される。
ここで、$P(H_1),\cdots,P(H_k)$はあらかじめ予想できる確率として事前確率と呼び、上式で求められる$P(H_i|A)$を$P(H_i)$に対して事後確率と呼ぶ。
「自然科学の統計学」における本問題の模範解答は、問題文中の以下の部分を誤った数字で解き進めたものです。
誤:それぞれ、$3:1,~1:1,~1:2$の比率で、
正:それぞれ、$3:1,~1:1,~2:1$の比率で、
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第9章 演習問題 P273
そのため、本記事の解説においては、問題文に記載の数字をもとに計算を行っているため、本書の解説と値が異なることをご了承ください。
大問1. (i)の解説
前提より、事前確率は
$$P(H_1) = P(H_2) = P(H_3) = \frac13$$
また、それぞれのツボ$H_1,~H_2,~H_3$を選んだときに、その壺から$S$を引く確率は
$$P(S|H_1) = \frac34$$
$$P(S|H_2) = \frac12$$
$$P(S|H_3) = \frac23$$
ここで、$\sum P(H_i)\cdot P(A|H_i)$を計算すると
$$\sum P(H_i)\cdot P(A|H_i) = \frac13 \times \frac34 + \frac13 \times \frac12 + \frac13 \times \frac23 = $\frac{23}{36}$
よって、ベイズの定理より、それぞれの事後確率は
$$P(H_1 |S) = \frac{ \frac13 \times \frac34}{\frac{23}{36}} = \frac{36}{23 \times 4} = \frac9{23}$$
$$P(H_2 |S) = \frac{ \frac13 \times \frac12}{\frac{23}{36}} = \frac{36}{23 \times 6} = \frac6{23}$$
$$P(H_3 |S) = \frac{ \frac13 \times \frac23}{\frac{23}{36}} = \frac{2 \times 36}{23 \times 9} = \frac8{23}$$
大問1の(ii)解説
(i)で選んだツボと同じ壺からもう一度玉を引く時、(i)の結果から、玉$S_2$を引く時点においては次のように事前確率が求められていることになります。
- 玉$S_1$を引いた時にその壺が$H_1$という事前確率$P(H_1|S_1) = \frac9{23}$
- 玉$S_1$を引いた時にその壺が$H_2$という事前確率$P(H_2|S_1) = \frac6{23}$
- 玉$S_1$を引いた時にその壺が$H_3$という事前確率$P(H_3|S_1) = \frac8{23}$
そして、つぼ$H_1,~H_2,~H_3$から玉$S_2$を引く確率は(i)と変わりがないので
$$P(S_2|H_1) = \frac34$$
$$P(S_2|H_2) = \frac12$$
$$P(S_2|H_3) = \frac23$$
ここで、$\sum P(H_1|S_1)\cdot P(S_2|H_1)$を計算すると
$$\sum P(H_1|S_1)\cdot P(S_2|H_1) = \frac9{23} \times \frac34 + \frac6{23} \times \frac12 + \frac8{23} \times \frac23 = \frac{181}{23\cdot 12}$$
よって、それぞれの事後確率は
$$P(H_1|S_1S_2) = \frac{\frac9{23} \times \frac34}{\frac{181}{23 \cdot 12}} = \frac{9 \times 3 \times 23 \times 12}{181\times 23 \times 4} = \frac{81}{181}$$
$$P(H_2|S_1S_2) = \frac{\frac6{23} \times \frac12}{\frac{181}{23 \cdot 12}} = \frac{6 \times 23 \times 12}{181\times 23 \times 2} = \frac{36}{181}$$
$$P(H_3|S_1S_2) = \frac{\frac8{23} \times \frac23}{\frac{181}{23 \cdot 12}} = \frac{8 \times 2 \times 23 \times 12}{181\times 23 \times 3} = \frac{64}{181}$$
大問1(iii)の解説
(i)(ii)では、玉$S_1$を引いた時のツボが$H_i$である事後確率を計算し、その事後確率を玉$S_2$を引く試行の事前確率として計算を行いました。
(iii)では連続して玉$S_1S_2$を引いた際のツボが$H_i$であるような事後確率を計算していきます。
つぼ$H_1,~H_2,~H_3$から連続して玉$S_1S_2$を引く確率は、復元抽出であることに注意すると
$$P(S_1S_2|H_1) = \left(\frac34\right)^2 = \frac9{16}$$
$$P(S_1S_2|H_2) = \left(\frac12\right)^2 = \frac14$$
$$P(S_1S_2|H_3) = \left(\frac23\right)^2 = \frac49$$
また、$P(H_1) = P(H_2) = P(H_3) = 1/3$に変わりはないので、
$\sum P(H_i)\cdot P(S_1S_2 |H_i)$を計算すると
$$\sum P(H_i)\cdot P(S_1S_2 |H_i) = \frac13 \left(\frac9{16} + \frac14 + \frac49\right) = \frac{181}{27 \cdot 16}$$
よって、求める事後確率$P(H_i\S_1S_2)$は
$$P(H_1|S_1S_2) = \frac{\frac13 \times \frac9{16}}{\frac{181}{27 \cdot 16}} = \frac{9 \times 27 \times 16}{181 \times 3 \times 16} = \frac{81}{181}$$
$$P(H_2|S_1S_2) = \frac{\frac13 \times \frac14}{\frac{181}{27 \cdot 16}} = \frac{ 27 \times 16}{181 \times 3 \times 4} = \frac{36}{181}$$
$$P(H_3|S_1S_2) = \frac{\frac13 \times \frac49}{\frac{181}{27 \cdot 16}} = \frac{4 \times 27 \times 16}{181 \times 3 \times 9} = \frac{64}{181}$$
この結果は(ii)の結果と一致します。
大問2の解説
求める確率$P(S)$は、1回目に玉$S_1$を引いたツボが$H_i$であったような時に、2回目も同じつぼから$S_2$を引く確率の全ての$i$についての和であるので、$\sum P(S_1|H_i)\cdot P(S_2|H_i)$に他なりません。
ここで、$\sum P(S_1|H_i)\cdot P(S_2|H_i)$は大問1の(ii)の途中で求めているのでこれを引用すると
$$\sum P(H_1|S_1)\cdot P(S_2|H_1) = \frac{181}{23\cdot 12} = \frac{181}{276}$$
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題1,2「ベイズの定理による確率の更新・予測分布」について解説してみました!
分数計算がかなりハードだったかと思いますが、事後確率と事前確率の関係性さえ理解してしまえばあとはゴリゴリ計算していくだけだったかと思います。
皆さんもぜひ事前確率という情報がある際には、原因の確率を推測する際にベイズの定理を活用してみてください!



コメント