
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題9「信頼性のベイズ的評価」についてPythonで解いていきたいと思います。
本問題は分布の畳み込みや尤度関数の計算、事後確率の導出など、今まで学習してきたことのそう復習的な側面があるので、腕試しに最適の問題となっております。
問題文
<信頼性のベイズ的評価>
i ) 指数分布, ガンマ分布の再生性$Ex(\lambda) * Ex(\lambda) = Ga(2, \lambda)$を証明せよ
ii ) ある工業用エンジンの故障時間は平均$\theta$の指数分布$Ex(1/\theta)$
$$f(x) = (1/\theta)e^{-x/\theta}$$
に従うとしよう。
2人の設計者A氏、B氏は共同でエンジンの改良設計を行うことになった。
仕様によれば、$\theta \geqq 3000(h)$とならねばならない.
ところで、a)過去に類似の実績のあるA氏によれば、このことは0.75で可能であるが、$\theta \leqq 2000$となる失敗ケースも小さい確率0.05でありうると思われた.
また、b) B氏はA氏ほど経験がなく、このような失敗は確率0.30で起こると考えた.
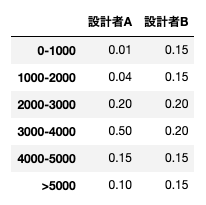
A氏は比較的楽観的、B氏は悲観的見方をしているわけであるが、詳しく言えば、A氏、B氏の$\theta$の事前確率分布$w_A(\theta), w_B(\theta)$は下表のようである.
$w_A(\theta), w_B(\theta)$のグラフを、$\theta$(横軸)の単位を$1000h. = 1$としてそれぞれ書け.
ただし、$>5000$の階級は、便宜的に$5000-6000$と考えよ.
iii ) 改良した試作型エンジン2機をテストして、故障時間が、$x_1 = 2000, x_2 = 2500$であった.
この標本和$t \equiv x_2 + x_2 = 4500$であるとき、A, Bの、$\theta$の事後確率分布
$$w’_A(\theta | 2000, 2500),~~w’_B(\theta | 2000, 2500)$$
を表と同様の形に求めよ.
なお、微積分学の知識から、
$$\int_a^b \frac{t}{\theta^2}e^{-t/\theta}d\theta = e^{-t/b}-e^{-t/a}~~(t>0, b \geqq a \geqq 0)$$
を用いてよい. $a=0$の時は、右辺第2項$=0$とする.
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第9章 演習問題 P273~274
指数分布
指数分布は確率密度関数
$$f(x) = \lambda e^{-\lambda x}dx~~(x \geqq 0),~~0~(x<0)$$
で定義される連続型の分布のこと
ガンマ分布
ガンマ分布は確率密度関数
$$f(x) = \frac{\lambda^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x} (x \geqq 0), ~~ 0~(x < 0)$$
ここで、
$$\Gamma(\alpha) = \int_0^{\infty} x^{\alpha -1}e^{-x}dx$$
であり、$\alpha$が自然数の時
$$\Gamma(\alpha) = (\alpha-1)!$$
確率分布の畳み込み
確率分布の畳み込み$k = g * h$は次のように定義される
$$k(z) = \int_{-\infty}^{\infty} g(x)h(z-x)dx$$
実装コード
本問題は以下のコードで解いていきます
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math
import numpy as np
df = pd.read_csv('Bayesian_evaluation_of_reliability.csv', index_col = 0)
indices = df.index
df = df.reset_index()
# グラフの可視化のためにインデックスを数値に、データを横持ちに
df['index'] = [0,1,2,3,4,5]
plot_df = df.melt('index')
display(plot_df)
# 棒グラフで可視化
plt.figure(figsize = (10,7))
sns.barplot(plot_df, x = 'index', y = 'value', hue = 'variable')
# 尤度を求める式
def calc_p(a, b):
eb = math.exp( - 4500 / b)
if a == 0:
ea = 0
else:
ea = math.exp( - 4500 / a)
p = eb - ea
return p
likelihood_df = pd.DataFrame()
likelihoods = []
# 実際に尤度を求める
for i in range(6):
a = i * 1000
b = (i + 1) * 1000
p = calc_p(a, b)
likelihoods.append(p)
print(f'{a} - {b}: 尤度p = {p}')
# 元データと結合するための調整
likelihood_df['index'] = range(6)
likelihood_df['likelihood'] = likelihoods
display(likelihood_df)
# 尤度を元データとmerge
df = pd.merge(df, likelihood_df,on = 'index')
df.index = indices
df = df.drop('index', axis = 1)
# 事後確率の初期設定
df['postpA'] = 0
df['postpB'] = 0
# 事後確率の計算
for index, row in df.iterrows():
sumA = np.array(df['設計者A']) @ np.array(df['likelihood']).reshape(6,-1)
sumB = np.array(df['設計者B']) @ np.array(df['likelihood']).reshape(6,-1)
df.at[index, 'postpA'] = row['設計者A'] * row.likelihood / sumA
df.at[index, 'postpB'] = row['設計者B'] * row.likelihood / sumB
display(df)(i)の解説
本書の解説ではモーメント母関数の観点から証明していますが、本記事においては畳み込みから計算していきたいと思います.
まずはガンマ関数の方から計算します。
$$f(x) = \frac{\lambda^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1$e^{-\lambda x} (x \geqq 0), ~~ 0~(x < 0)$
であるから、
$$Ga(\alpha = 2, \lambda) = \frac{\lambda^2}{\Gamma(2)} \cdot x^1 e^{-\lambda x}$$
ここで、$\Gamma(2) = 1! = 1$であるから、
$$Ga(\alpha = 2, \lambda) = \lambda^2 x e^{-\lambda x}$$
また、指数分布の畳み込みについて考えると,
$$Ex(\lambda)*Ex(\lambda) = \int_{-\infty}^{\infty} f(z)f(x-z)dz$$
ここで、指数関数の定義より$z < 0$または$x-z<0$においては$f(z)=0$であるので、
0以外の値を持つ積分範囲は$0 \geqq z \geqq x$
よって、
$$Ex(\lambda)*Ex(\lambda) = \int_{-\infty}^{\infty} f(z)f(x-z)dz = \int_{0}^{x} f(z)f(x-z)dz$$
$$= \int_0^x \lambda e^{z} \times \lambda e^{x-z} dz = \lambda^2 e^x \int_0^x 1dz$$
$$= \lambda^2 e^x \left[z\right]_0^x = \lambda^2 xe^x$$
よって、上の2つの計算により
$$Ex(\lambda) * Ex(\lambda) = Ga(2, \lambda)$$
が導かれる
(ii)の解説
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math
import numpy as np
df = pd.read_csv('Bayesian_evaluation_of_reliability.csv', index_col = 0)
indices = df.index
df = df.reset_index()
display(df)
# グラフの可視化のためにインデックスを数値に、データを横持ちに
df['index'] = [0,1,2,3,4,5]
plot_df = df.melt('index')
display(plot_df)
# 棒グラフで可視化
plt.figure(figsize = (10,7))
sns.barplot(plot_df, x = 'index', y = 'value', hue = 'variable')元々のデータフレームは以下になります。
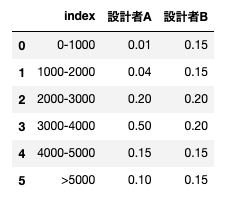
データをうまいこと可視化するために、DataFrame.melt()を使ってデータを横持ちに変換しています
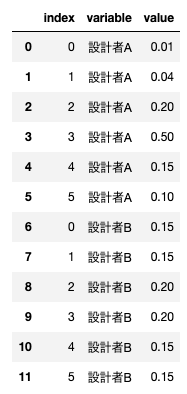
最後にseaborn.barplot()を使用して、設計者AとBの事前確率を棒グラフで可視化しています
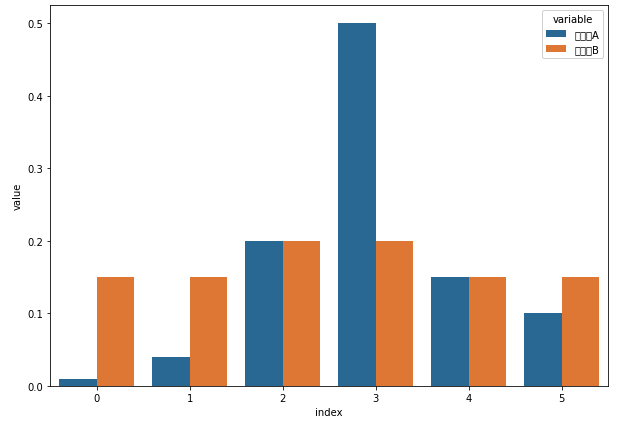
(iii)の解説
# 尤度を求める式
def calc_p(a, b):
eb = math.exp( - 4500 / b)
if a == 0:
ea = 0
else:
ea = math.exp( - 4500 / a)
p = eb - ea
return p
likelihood_df = pd.DataFrame()
likelihoods = []
# 実際に尤度を求める
for i in range(6):
a = i * 1000
b = (i + 1) * 1000
p = calc_p(a, b)
likelihoods.append(p)
print(f'{a} - {b}: 尤度p = {p}')
# 元データと結合するための調整
likelihood_df['index'] = range(6)
likelihood_df['likelihood'] = likelihoods
display(likelihood_df)
# 尤度を元データとmerge
df = pd.merge(df, likelihood_df,on = 'index')
df.index = indices
df = df.drop('index', axis = 1)
# 事後確率の初期設定
df['postpA'] = 0
df['postpB'] = 0
# 事後確率の計算
for index, row in df.iterrows():
sumA = np.array(df['設計者A']) @ np.array(df['likelihood']).reshape(6,-1)
sumB = np.array(df['設計者B']) @ np.array(df['likelihood']).reshape(6,-1)
df.at[index, 'postpA'] = row['設計者A'] * row.likelihood / sumA
df.at[index, 'postpB'] = row['設計者B'] * row.likelihood / sumB
display(df)本問題は以下3ステップで解いています
- 尤度関数を求める式を導出する
- 具体的な尤度を求める
- 事後確率を計算する
順を追って解説していきます
尤度関数を求める式を導出する
(i)から
$$Ex(\lambda) * Ex(\lambda) = Ga(2, \lambda)$$
であることがわかっています。
ここで、本問題においては$\lambda = \frac1{\theta}$であるから、試作型エンジン2機の故障確率は1台ずつの故障確率の分布$f(x)$の畳み込みと考えることができるので、
$$Ex(\frac1{\theta}) * Ex(\frac1{\theta}) = Ga(2, \frac1{\theta}) = \frac{x}{\theta^2}e^{-x/\theta}$$
ここで、平均$\theta$の範囲が時間$t$が$a$から$b$までの故障確率の尤度は
$$\int_a^b \frac{t}{\theta^2}e^{-t/\theta}d\theta$$
として計算できるが、本問題中記載の微積分学から導出できる式により、
$$\int_a^b \frac{t}{\theta^2}e^{-t/\theta}d\theta = e^{-t/b} – e^{-t/a}$$
として計算することができる.
また、今回の問題では故障時間は標本和より$t=4500$と置くことができるので、求める尤度関数は
$$e^{-4500/b} – e^{-4500/a}$$
である
具体的な尤度を求める
上記で導出された尤度関数を使って、具体的な尤度の値を時間$1000h$刻みの範囲で求めていきます.
# 尤度を求める式
def calc_p(a, b):
eb = math.exp( - 4500 / b)
if a == 0:
ea = 0
else:
ea = math.exp( - 4500 / a)
p = eb - ea
return p
likelihood_df = pd.DataFrame()
likelihoods = []
# 実際に尤度を求める
for i in range(6):
a = i * 1000
b = (i + 1) * 1000
p = calc_p(a, b)
likelihoods.append(p)
print(f'{a} - {b}: 尤度p = {p}')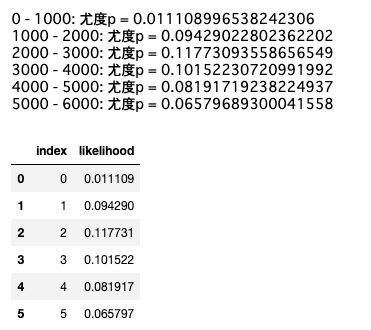
事後確率を計算する
# 尤度を元データとmerge
df = pd.merge(df, likelihood_df,on = 'index')
df.index = indices
df = df.drop('index', axis = 1)
# 事後確率の初期設定
df['postpA'] = 0
df['postpB'] = 0
# 事後確率の計算
for index, row in df.iterrows():
sumA = np.array(df['設計者A']) @ np.array(df['likelihood']).reshape(6,-1)
sumB = np.array(df['設計者B']) @ np.array(df['likelihood']).reshape(6,-1)
df.at[index, 'postpA'] = row['設計者A'] * row.likelihood / sumA
df.at[index, 'postpB'] = row['設計者B'] * row.likelihood / sumB
display(df)設計者ごとの事前確率と先ほど求めた尤度を使用して、事後確率を求めていきます。
事後確率は事前確率を$w(\theta_i)、尤度関数を$f(z|\theta)$とすると、以下の式によって計算することができます.
$$w'(\theta_i | z) = \frac{w(\theta_i) \cdot f(z|\theta_i)}{\sum_j w(\theta_i) \cdot f(z|\theta_i) }$$
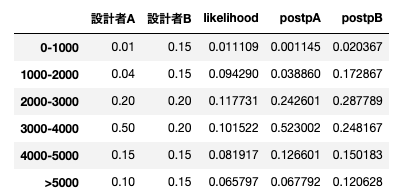
これによって、経験則的な事前確率と故障確率を表す尤度関数とを組み合わせて、尤もらしい事後確率を導出することができました.
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題9「信頼性のベイズ的評価」についてPythonで解いていきました。
統計学入門で学んだ指数分布・ガウス分布・確率分布の畳み込みや、本章で学んだ事後確率の導出を用いた複合的な問題だったかと思います。
皆さんも求めたい値が何らかの分布を仮定でき、そこに経験則的な事前確率が存在する場合は、今回のような計算を使って尤もらしい事後確率を求めてみてください!



コメント