
元教師
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
この記事では書籍「自然科学の統計学」(東京大学出版会)における各種データをCSV形式で掲載しています。
なお、本記事に掲載されているデータは東京大学教養学部統計学教室編者『自然科学の統計学』(東京大学出版会/2001)を参考にブログ主がPythonで作成したものになります。
RやPythonで可視化・分析したい際にはお役立てください!
- CSVデータの使い方
- 第1章 確率の基礎
- 第2章 線形モデルと最小二乗法
- 第3章 実験データの分析
- 第4章 最尤法
- 第5章 適合度検定
- 0, 1, …, 9の乱数発生度数(P146)
- 到達α粒子データへのポアソン分布あてはめ(P149)
- ドラム缶製造工程の溶接不良の比較(P153)
- 予防注射の効果(P153)
- 職業別に分類した初登院時のガンの症状(P156)
- 官能検査データ(P162)
- 英国における投票の推移を表すデータ(P164)
- 左右の裸眼視力の4階級分類データ(P165)
- 1981年パ・リーグ勝敗表(P167)
- 混紡洋服地の評価(P171)
- 【演習5.2】疑似乱数の適合度検定(P174)
- 【演習5.4】適合度検定:試合数の分布(P175)
- 【演習5.5】適合度検定:得点データへの分布のあてはめ(P175)
- 【演習5.6】ブラッドリー・テリーのモデル(P175,176)
- 【演習5.7】πの数字の一様性(P176)
- 第6章 検定と標本の大きさ
- 第7章 分布の仮定
- 第8章 質的データの統計的分析
- 第9章 ベイズ決定
- 第10章 確率過程の基礎
- まとめ
CSVデータの使い方
Pythonで可視化・分析を行う際には、以下のようにPandasでデータを取り込んでからご活用ください。
import pandas as pd
df = pd.read_csv('[各種データ名].csv')Rで可視化・分析を行う際には、以下のようにPandasでデータを取り込んでからご活用ください。
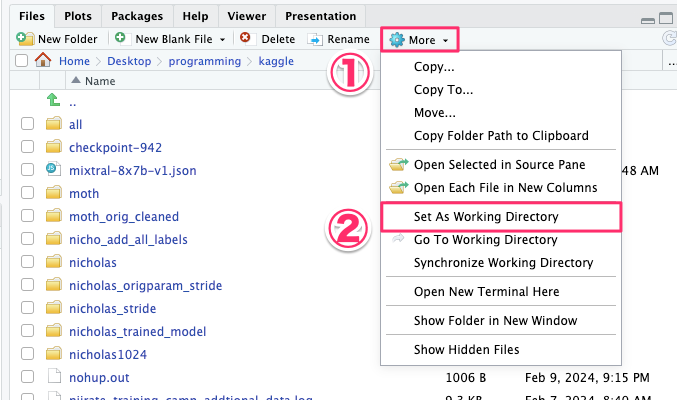
data <- read.csv('[各種データ名].csv')なお、RでCSVデータを読み込む際には以下から「Files」からCSVデータのあるディレクトリに移動して、More > Set As Working Directory の順にクリックをして、作業環境とCSVデータのある場所を同一にしてから作業すると、より作業効率がよくなるでしょう。
第1章 確率の基礎
バクテリアの数(P11)
プロシャの兵士の数(P22)
第2章 線形モデルと最小二乗法
脂肪の種類に対応する吸収量(P34)
液体のある成分と曇り点の関係(P35)
コンクリートの養生の温度条件と圧縮強度の関係(P46)
演習2.4:データの比較(P75)
演習2.6:2変量データと回帰分析(P76)
演習2.7:2変量データと回帰分析(P77)
演習2.8:2変量データと回帰分析 2標本(P77)
第3章 実験データの分析
2標本問題データ:ラットの体重(g)(P79)
製品1kg中の成分量(P85)
交互作用がない場合の応答(P95)
交互作用がある場合の応答(P95)
繰り返しのある2元配置データ:圧延製品の引張り強さ(P97)
圧延条件データ(P99)
熱処理歪み(P105)
【演習3.1】2標本問題(P108)
【演習3.2】一元配置(P108)
【演習3.6】繰り返しのある2元配置(P109)
第4章 最尤法
大学への距離とキャンパス内に住む比率の関係(P114)
期末試験成績のデータ(P114)
えんどう豆の4分類データ(P133)
【演習4.1】心理学データ(P142)
【演習4.2】幾何分布の最尤推定(P142)
【演習4.4】指数分布の最尤推定(P143)
第5章 適合度検定
0, 1, …, 9の乱数発生度数(P146)
到達α粒子データへのポアソン分布あてはめ(P149)
ドラム缶製造工程の溶接不良の比較(P153)
予防注射の効果(P153)
職業別に分類した初登院時のガンの症状(P156)
官能検査データ(P162)
英国における投票の推移を表すデータ(P164)
左右の裸眼視力の4階級分類データ(P165)
1981年パ・リーグ勝敗表(P167)
混紡洋服地の評価(P171)
【演習5.2】疑似乱数の適合度検定(P174)
【演習5.4】適合度検定:試合数の分布(P175)
【演習5.5】適合度検定:得点データへの分布のあてはめ(P175)
【演習5.6】ブラッドリー・テリーのモデル(P175,176)
【演習5.7】πの数字の一様性(P176)
第6章 検定と標本の大きさ
1988年8月の東京と大阪における最高気温(P184)
第7章 分布の仮定
締め付けトルク(P201)
ラットの肺重量(P203)
各国の人口と面積(P216)
【演習問題7.4】幹葉表示とロバスト推定(P229)
【演習問題7.5】対称性の符号検定(P229)
【演習問題7.6】2標本問題と順位和検定(P229)
【演習問題7.7】正規性の仮定のチェック(P229)
第8章 質的データの統計的分析
薬物濃度と生物の死亡数(P232)
個別ケース別の対数濃度$X_i$、死亡・生存の別$Y_i$(P232)
プロビット,ロジットモデルによる投与量別死亡確率(P243)
学生のA,Bの2コースの選択(P245)
【演習問題8.5】市場調査(P250)
第9章 ベイズ決定
ネルソン氏の状況(P266)
フィッシャーによるアイリス・データ(P271)
【演習問題9.5】ベイズ診断(P273)
【演習問題9.9】信頼性のベイズ的評価(P275)
第10章 確率過程の基礎
株価データのブラウン運動仮説の検証(P301)
まとめ
書籍「自然科学の統計学」に登場し、なおかつ書籍の中でデータを使った何かしらの計算、可視化等を行なっているCSVデータについては一通り作成しました!
「このデータも作って欲しい!」等の要望があれば可能な限り対応しますのでコメント欄にご記載ください!
これらのデータを使って、「自然科学の統計学」の内容をただ読むだけでなく、ご自身の手で計算、可視化、分析を行なってみることをお勧めします!



コメント