最も分かり易いディープラーニングの書籍といえば！『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』から得た学び3選

元教師

こんにちは！データサイエンティストの青木和也（https://twitter.com/kaizen_oni）です！

今回の記事では、深層学習の仕組みについて知りたい人は読まない理由がないほどの名著、通称ゼロつくと呼ばれている『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』から得た学びを3つ厳選してご紹介しようと思います。

本書は、機械学習関連の書籍を複数冊読んできたブログ主も「これほどまでに分かりやすく深層学習について書かれた本はなかった」と感動するレベルで、ディープラーニングについて作りながら学べる良書になっています。

本記事が、本書の購入を考えている方の参考になれば幸いです！

本書の概要
本書から得た学び
まとめ

本書の概要

本書の特徴は「作る」という過程を通じて、ディープラーニングの本質に迫ろうという点にあります。ディープラーニングのプログラムを実装する過程を通して、必要な技術を（できるだけ）省略することなく説明していきます。
斎藤康毅『ゼロから作るDeepLearning | Pythonで学ぶディープラーニングの理論と実装』（オライリー・ジャパン/2017） iii

本書はゼロつくシリーズの始祖ともいうべき1冊であり、その後のシリーズが「生成モデル」というごく最近のトレンドまで末長く続いていることからも、本書が多くのデータサイエンティスト・AIエンジニアに受け入れられている1冊であることが分かります。

深層学習の書籍では、どうしても数式による解説が必要になってしまうため、解説が難解になってしまうことも多いですが、本書は数式の解説も分かりやすく、実装も分かりやすいという特例中の特例の書籍です。

本書の構成は以下のようになっています。

1章 Python入門
2章パーセプトロン
3章ニューラルネットワーク
4章ニューラルネットワークの学習
5章誤差逆伝播法
6章学習に関するテクニック
7章畳み込みニューラルネットワーク
8章ディープラーニング
付録A Softmax-with-Lossレイヤの計算グラフ

本書は、深層学習初学者にもお勧めですが、他の機械学習書籍を読んでから読むと点と点が繋がるような感覚を覚えるので、深層学習をある程度学んだ方にもお勧めです。

本書から得た学び

本書から得た学びは以下のとおりです。

誤差逆伝播法の計算グラフでの表現方法
深層学習における最適化のイメージと数式
なぜ二乗和誤差や交差エントロピーを損失関数として使うのか

順を追って解説していきましょう。

誤差逆伝播法の計算グラフでの表現方法

本書においては、「誤差逆伝播法」という「後ろから微分値が前に伝わってパラメータが修正される」というざっくりとした理解しかできていないものを、計算グラフというツールを使うことによって鮮やかに理解させてくれています。

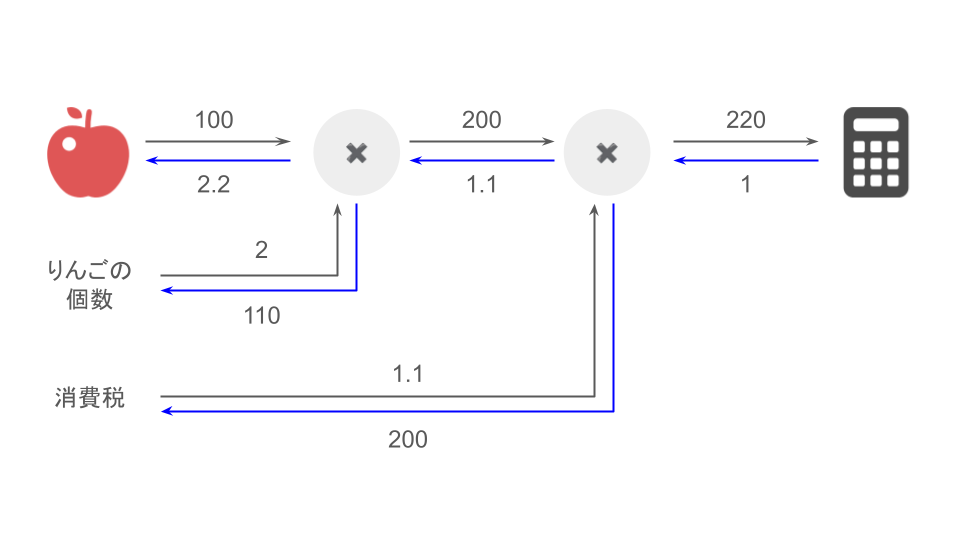
本書における誤差逆伝播法の説明の鮮やかポイントは以下の6つです。

「加算ノードは微分値がそのまま伝わる」「乗算ノードは入力信号を反転してかけ算する」という単純なルールで誤差逆伝播法を説明している
「りんごのお買い物の事例」で見事に誤差逆伝播法を説明している
各レイヤーのforward（順伝播）とbackward（逆伝播）の実装がめちゃくちゃ分かりやすいし、対応関係も分かりやすい
「誤差逆伝播法において、ReLUはスイッチ」という説明の神さ
backward（逆伝播）の実装と解析的背景が結びついている感動
DropoutやCNNのbackward（逆伝播）の実装まで分かりやすいという神仕様

おそらく上記6つだけではなく、もっと小刻みに感動しているはずです。

機械学習に関する書籍を読んでいて、読者を全く舐めていないにも関わらず、ここまで分かり易い本は初めて出会ったので、「誤差逆伝播法」を真に理解したい方は本書を必ず読んでください。

深層学習における最適化のイメージと数式

本書では機械学習を学んでいる上でなんとなく理解してやりすごすランキングで言えば、誤差逆伝播法と上位を争う「SGD（確率的勾配降下法）」や「Adam」などのパラメータの最適化手法についても、実際に実装をしながら、分かりやすく解説してくれています。

本書における、パラメータ最適化手法の説明の感動ポイントは以下の6つです。

Kaggle等で度々出てきていたoptimizer、お前そういうことだったのか、と納得する
最適化手法の実装がめちゃくちゃ分かり易く、今までなんとなく使っていたupdate関数が可愛く思える
選択授業で物理を取っていた人間には、Momentumのお椀のイメージと速度/加速度は刺さる
Adamの命名の謎が解ける
計算グラフのおかげで「パラメータの初期値は0じゃダメ」に首もげるほど納得する
「パラメータの初期値適切に設定しないと勾配消失する問題」に初めて触れるのにとても分かり易い

誤差逆伝播法で導入した計算グラフが最適化手法でも効いてくるところが本書の美しいところです。

パラメータ最適化について真に理解したい方も本書を必ず読んでください。

なぜ二乗和誤差や交差エントロピーを損失関数として使うのか

第5章誤差逆伝播法では、手書き数字の正しい数字ラベルを判定するためにソフトマックス関数で各数字の確率を出力し、次のレイヤーに損失関数として交差エントロピー誤差を設定しています。

交差エントロピー誤差とは、出力層が$n$個であり、予測確率が$0 ¥leqq y_1, \cdots, y_n \leqq$、正解ラベルが$t_1, \cdots, t_n \in (0,1)$であるようなとき、以下のように計算します。

$$L = \sum_{i=1}^n t_i \log y_i$$

そして、Softmaxレイヤーと交差エントロピー損失レイヤーを逆伝播した誤差の値は

$$(y_1 – t_1, \cdots, y_n – t_n)$$

のような「予測値と正解ラベルの差分」を表した値となっており、非常にキレイなのです。

さらに驚くべきことは、本書の中の補足に以下のように書かれていることです。

「ソフトマックス関数」の損失関数として「交差エントロピー誤差」を用いると、逆伝播が$(y_1- t_1, y_2-t_2,y_3-t_3)$という”キレイ”な結果になりました。
実は、そのような”キレイ”な結果は偶然ではなく、そうなるように交差エントロピー誤差という関数が設計されたのです。
斎藤康毅『ゼロから作るDeepLearning | Pythonで学ぶディープラーニングの理論と実装』（オライリー・ジャパン/2017） P155

これまで、「深層学習の損失関数には交差エントロピーを使用する」ということは、実装をしながら機械学習を学ぶ教材などで学んでいたのですが、まさか交差エントロピーが「逆伝播の値がキレイになるから」という美しい理由で設定されていたなどとは夢にも思わなかったので、驚きがありました。

先ほどの補足には「恒等関数の損失関数に二乗和誤差を設定するのも、逆伝播が$y_1-t_1$のようになってくれるから」と、さらっと書いてあり、今まで学んできたことの線が繋がる感覚があり、とても爽快です。

「深層学習の損失関数ってなんで交差エントロピーなん？」という疑問を一度でも抱いたことがある方は、本書の付録A「Softmax-with-Lossレイヤの計算グラフ」を読んで、「ほんまや…！」となっていただくことをお勧めいたします。