
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第10章-演習問題3「行動科学的モデル」について丁寧に解説していきたいと思います。
ある動物の取る戦略が愚かであるか賢いかによって、欲しいゴールに辿り着くまでにどれだけの手数がかかるかを推移確率を元に考える問題です。
とはいえ、やっていることは高校数学の域を出ないので、高校数学の確率の復習をしたい方はぜひチャレンジしてみてください!
問題文
<行動科学的モデル>
4個の箱がある。
一つの箱には食物が入っている。
残りの3つの箱は触ると、電気ショックを感じる。
今3匹のネズミが食物にありつくため箱を開けようとしている。
‘愚かな’ネズミ 毎回でたらめに各箱を開けようとする ‘普通の’ネズミ 直前に試みた箱は除いて、残り3つの箱をでたらめに開けようとする ‘利口な’ネズミ 過去に試みた箱はすべて除いて、残りの箱をでたらめに開けようとする i ) 4個の箱に、1,2,3,4と番号をつける。番号1の箱に食物が入っている。
普通のネズミが$n$回目に開ける箱を$X_n$とする。
$X_n$の推移確率を求めよ。
ただし、食物の入っている箱がわかったあとは終生忘れないとする。
ii ) 各ねずみが食物にありつくまでの試行回数の期待値を求めよ.
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第10章 P305
推移確率とは?
ある1回の操作のうちに、ある状態$j$からある状態$k$に移る確率
$$p_{jk} = P(X_{n+1} = k | X_n = j)$$
のことを推移確率という。
(i)の解説
$X_n$の推移確率を考える上で注意すべきは以下2点である、
- ‘普通’のネズミは直前に試みた箱は除いて、残り3つの箱をでたらめに開けようとする
- 食物の入っている箱がわかったあとは終生忘れない
これに注意して、番号1,2,3,4にいる状況から、どこに移る可能性があるかを図示すると下図のようになる。
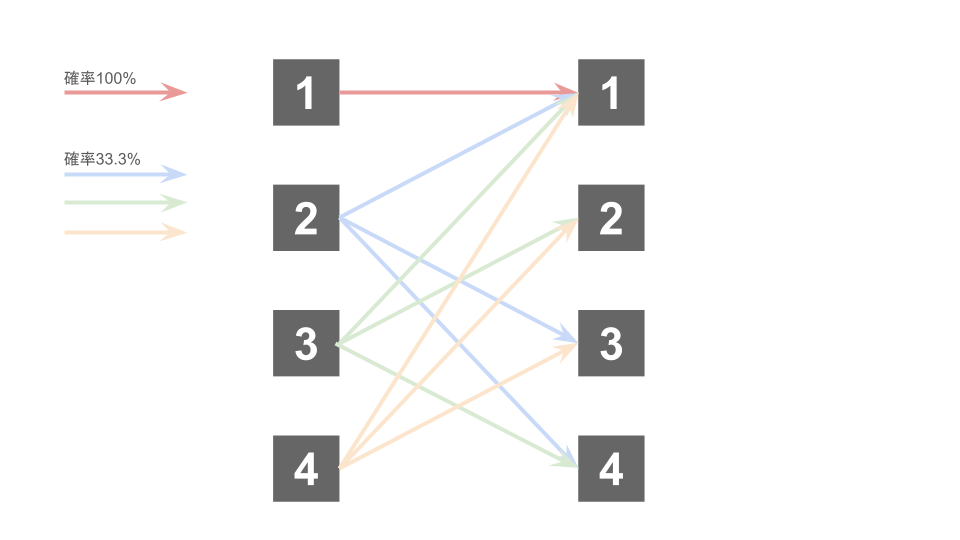
よって、上図を推移確率として書き起こすと、以下のようになる。
$$p_{jk} = 1~~~(j = k = 1)$$
$$p_{jk} = \frac13~~~(j \ne 1, j \ne k)$$
$$p_{jk} = 0~~~(その他)$$
(ii)の解説
‘愚かな’ネズミの試行回数の期待値
愚かなネズミについて、具体的に以下の4つの状況について考えてみよう.
- 試行1回目で初めて箱1を選ぶ
- 試行2回目で初めて箱1を選ぶ
- 試行3回目で初めて箱1を選ぶ
- 試行$n$回目で初めて箱1を選ぶ
試行1回目で初めて箱1を選ぶ
試行1回目について考えてみると、どの箱を選ぶ確率も等しいので、箱1を選ぶ確率は$\frac14$、当然ながら他の箱を選ぶ確率も$\frac14$であることがわかる。
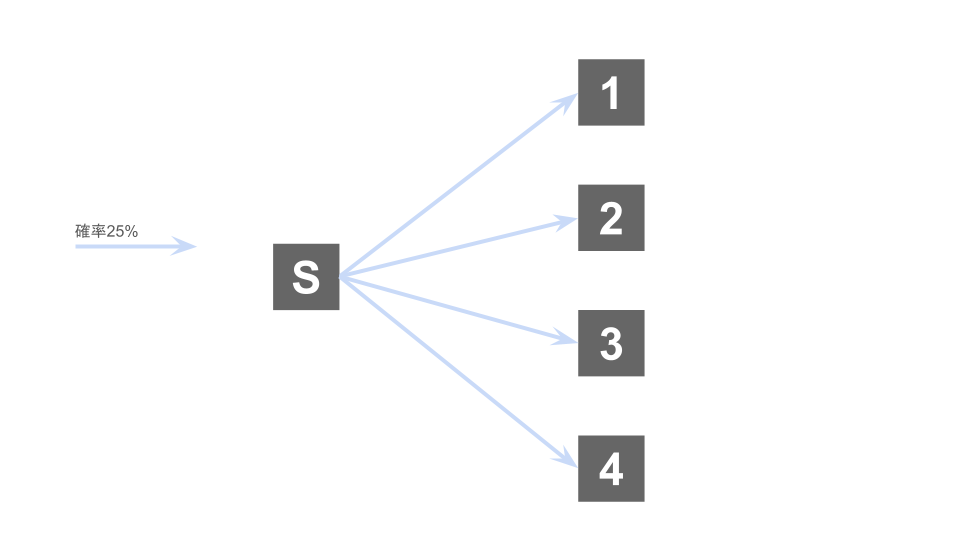
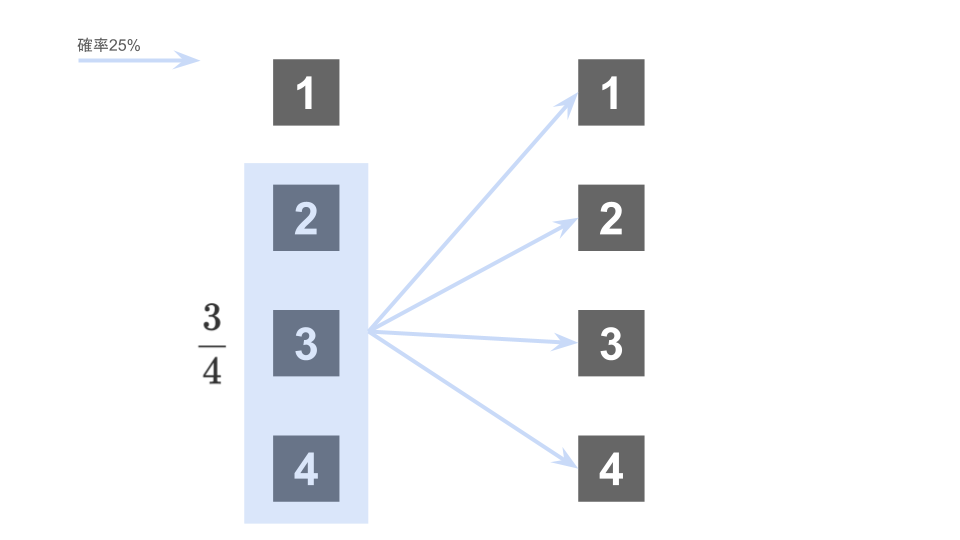
試行2回目で初めて箱1を選ぶ
2回目で初めて箱1を選ぶ確率を考えると、1回目では箱1以外の3つの箱のいずれかを選んでいる必要がある。
つまり、1回目で箱1以外の箱を選ぶ確率は$\frac34$である。
そして、2回目では箱1を選ぶ必要があるのだが、1回目が箱1以外であった時に、2回目に箱1を選ぶ確率は’愚かな’ネズミであることから$\frac14$とわかる。
よって、2回目で初めて箱1を選ぶ確率は
$$\frac34\times\frac14 = \frac3{16}$$
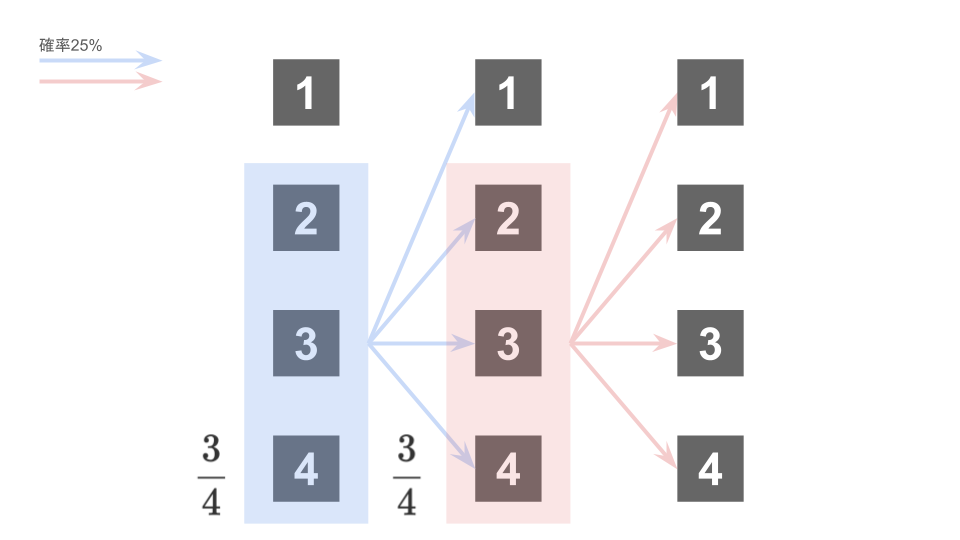
試行3回目で初めて箱1を選ぶ
試行3回目で初めて箱1を選ぶ、ということは試行1回目・2回目では箱1以外を選ぶ続け、3回目でようやく箱1を選ぶ必要がある。
よって、求める確率は
$$\left(\frac34\right)^2\times \frac14 = \frac9{64}$$
試行3回目で初めて箱1を選ぶ
先ほどまでの議論から、試行$n$回目で初めて箱1を選ぶ確率は以下のような式で表されることがわかる。
$$\frac14\cdot \left(\frac34\right)^{n-1}$$
試行回数の期待値を求める
試行回数の一般項が求められたところで、試行回数の期待値を求めていきたいと思う。
試行回数の期待値$E(X)$は次の式で表される。
$$E(X) = \sum_{n=1}^{\infty} \frac{n}4\cdot \left(\frac34\right)^{n-1}$$
ここで、$S_n = \sum_{k = 1}^n k\left(\frac34\right)^{k-1}$とすると
$$S_n = 1 + 2\times \frac34 + 3 \times \left(\frac34\right)^2 + \cdots ~~+ n \left(\frac34\right)^{n-1}$$
$$\frac34 S_n = ~~~~1\times \frac34 + 2 \times \left(\frac34\right)^2 + \cdots + (n-1)\left(\frac34\right)^{n-1} + n\left(\frac34\right)^n$$
$S_n – \frac34 S_n$をすると、
$$\frac14 S_n = 1 + \frac34 + \left(\frac34\right)^2 + \cdots + \left(\frac34\right)^{n-1} – n \left(\frac34\right)^n$$
$$=\sum_{k = 1}^n \left(\frac34\right)^{k-1} – n\left(\frac34\right)^n$$
$$=\frac{1 – \left(\frac34\right)^n}{1 – \frac34} – n\left(\frac34\right)^n$$
$$=4 – 4\left(\frac34\right)^n – n\left(\frac34\right)^n$$
よって、
$$S_n = 16 – 16\left(\frac34\right)^n – 4n\left(\frac34\right)^n$$
$n\to \infty$とすると、
$$\lim_{n\to \infty}S_n = 16$$
よって、
$$E(X) = \frac{16}4 = 4$$
分布を利用した解法
実は、初項$p$、公比$q$の形で表される確率分布
$$f(x) = pq^{x-1}$$
を幾何分布という。
幾何分布の期待値は$\frac1p$であるから、$p=\frac14$より、求める期待値は4であるとすぐにわかる。
本書ではこちらの解法が解答例として載っている。
‘普通の’ネズミの試行回数の期待値
‘普通の’ネズミについても’愚かな’ネズミと同様に考える.
- 試行1回目で初めて箱1を選ぶ
- 試行2回目で初めて箱1を選ぶ
- 試行3回目で初めて箱1を選ぶ
- 試行$n$回目で初めて箱1を選ぶ
試行1回目で初めて箱1を選ぶ
試行1回目については、’愚かな’ネズミと同じく$\frac14$の確率で箱1を選択する
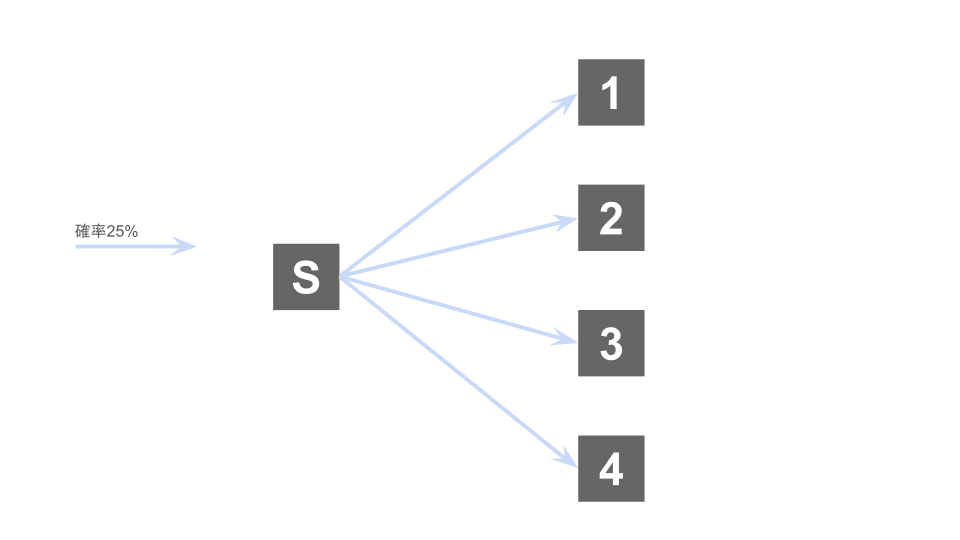
試行2回目で初めて箱1を選ぶ
ここからが’愚かな’ネズミと異なる点である。
試行2回目で初めて箱1を選ぶ確率は次の2つの確率を掛け合わせることによって求めることができる
- 試行1回目で箱1を選ばない確率
- 試行2回目で箱1を選ぶ確率
「試行1回目で箱1を選ばない確率」については、「試行1回目で箱1を選ぶ確率」の余事象であるので、$1-\frac14 =\frac34$である。
「試行2回目で箱1を選ぶ確率」については、’普通の’ネズミの「直前に試みた箱は除いて、残り3つの箱をでたらめに開けようとする」という特性に気をつけると、直前に選んだ箱以外の3つから1つをランダムに選び、その中の1つが箱1であるので、$\frac13$であることがわかる。
よって、求める確率は
$$\frac34 \times \frac13 = \frac14$$
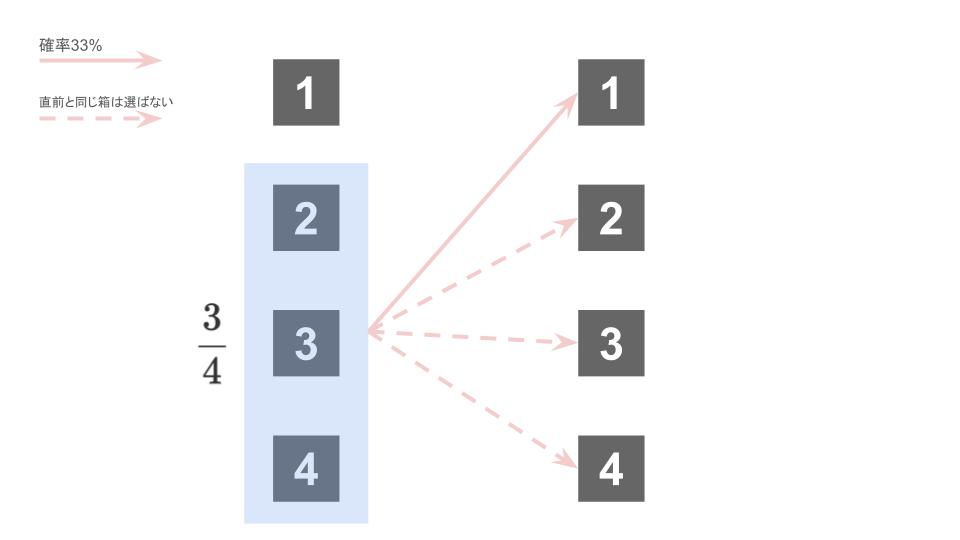
試行3回目で初めて箱1を選ぶ
試行3回目で初めて箱1を選ぶ確率は、次の3つの確率の掛け合わせで計算することができる。
- 試行1回目で箱1以外を選ぶ確率
- 試行2回目も箱1以外を選ぶ確率
- 試行3回目で箱1を選ぶ確率
「試行1回目で箱1以外を選ぶ確率」は$\frac14$であるが、「試行2回目も箱1以外を選ぶ確率」は「試行2回目で箱1を選ぶ確率」の排反事象と考えると、その確率は$1 – \frac13 = \frac23$と求められる。
また、試行3回目で箱1を選ぶ確率も2回目同様$\frac13$であるから、求める確率は
$$\frac34 \times \frac23 \times \frac13 = \frac16$$
試行$n$回目で初めて箱1を選ぶ
先ほどの「試行3回目で初めて箱1を選ぶ」の発想を$n$回に広げて考えてみよう。
つまり、考えるべき確率は以下の掛け合わせであることがわかる。
- 試行1回目で箱1以外を選ぶ確率
- 試行2回目も箱1以外を選ぶ確率
- 試行3回目も箱1以外を選ぶ確率
- $\cdots$
- 試行$n-1$回目も箱1以外を選ぶ確率
- 試行$n$回目で箱1を選ぶ確率
ここで、「試行1回目で箱1以外を選ぶ確率」であった。
一方で、それ以降の「試行2回目も箱1以外を選ぶ確率」「試行3回目も箱1以外を選ぶ確率」はすべて同一の確率$\frac23$となる。
これは’普通の’ネズミの「直前に試みた箱は除く(=残り3個の中から選ぶ)」という特性に由来している。
また、「試行2回目も箱1以外を選ぶ確率」から「試行$n-1$回目も箱1以外を選ぶ確率」は合計$n-2$回であることには注意が必要である。
よって、求める確率は
$$\frac34 \times \left(\frac23\right)^{n-2} \times \frac13$$
一般項を考える
ここで、’普通の’ネズミの一般項を考えてみる。
この時、’普通の’ネズミの「直前に試みた箱は除いて、残り3つの箱をでたらめに開けようとする」という性質から、試行1回目の一般項と試行2回目以降の一般項は異なることがわかる。
なぜなら、試行1回目で箱を選ぶときは何の情報もないので4つの箱の中から1つ選ぶが、試行2回目以降は直前の箱に食物がないことを知っているので、3つの箱の中から1つの箱を選ぶことになる。
よって、
| 試行1回目の時の確率 | $\frac14$ |
| 試行2回目以降$n$回目の時の確率 | $\frac34 \times \left(\frac23\right)^{n-2} \times \frac13$ |
試行回数の期待値を求める
先ほど立てた一般項から試行回数の期待値$E(X_n)$を求めると、次のようになる。
$$E(X) = \frac14 + \sum_{n =2}^{\infty} n\times \frac34 \times \left(\frac23\right)^{n-2} \times \frac13 = \frac14 + \frac14\sum_{n =2}^{\infty} n\times \left(\frac23\right)^{n-2} $$
ここで、$S_n = \sum_{k = 2}^n k\left(\frac23\right)^{k-2}$とおくと
$$S_n = 2 + 3 \cdot \frac23 + 4 \left(\frac23\right)^{2} + \cdots + n\left(\frac23\right)^{n-2}$$
$$\frac23S_n = ~~~~ 2 \left(\frac23\right) + 3 \left(\frac23\right)^{2} + \cdots + (n-1)\left(\frac23\right)^{n-2} + n\left(\frac23\right)^{n-1} $$
$S_n – \frac23 S_n$を計算すると
$$\frac13 S_n = 2 + \frac23 + \left(\frac23\right)^{2} + \cdots + \left(\frac23\right)^{n-2} – n\left(\frac23\right)^{n-1} $$
$$= 2 + \sum_{k = 1}^{n-1} \left(\frac23\right)^{k} -n \left(\frac23\right)^{n-1} $$
$$= 2 + \frac23 \cdot \frac{1 – \left(\frac23\right)^{n} }{1- \frac23} – n\left(\frac23\right)^{n-1} $$
$$ = 2 + 2 – 2\left(\frac23\right)^{n} – n\left(\frac23\right)^{n-1} $$
よって、
$$S_n = 6 + 6 – 6 \left(\frac23\right)^{n} – 3n\left(\frac23\right)^{n-1} $$
$n \to \infty$とすると、
$$\lim_{n\to \infty} S_n = 12$$
よって、求める試行回数の期待値$E(X)$は
$$E(X) = \frac14 + \frac{12}4 = \frac{13}4$$
‘利口な’ネズミの試行回数の期待値
‘利口な’ネズミについては、1試行ずつ箱1を選ぶ確率を求め、期待値を計算することができる。
なぜなら、’利口な’ネズミは「過去に試みた箱」のすべての情報を持つからである。
よって、’利口な’ネズミは最大でも4回以内には箱1を選ぶことができることがわかる。
- 試行1回目で初めて箱1を選ぶ確率
- 試行2回目で初めて箱1を選ぶ確率
- 試行3回目で初めて箱1を選ぶ確率
- 試行4回目で初めて箱1を選ぶ確率
試行1回目で初めて箱1を選ぶ確率
試行1回目で初めて箱1を選ぶ確率は、他のネズミと同様に$\frac14$である
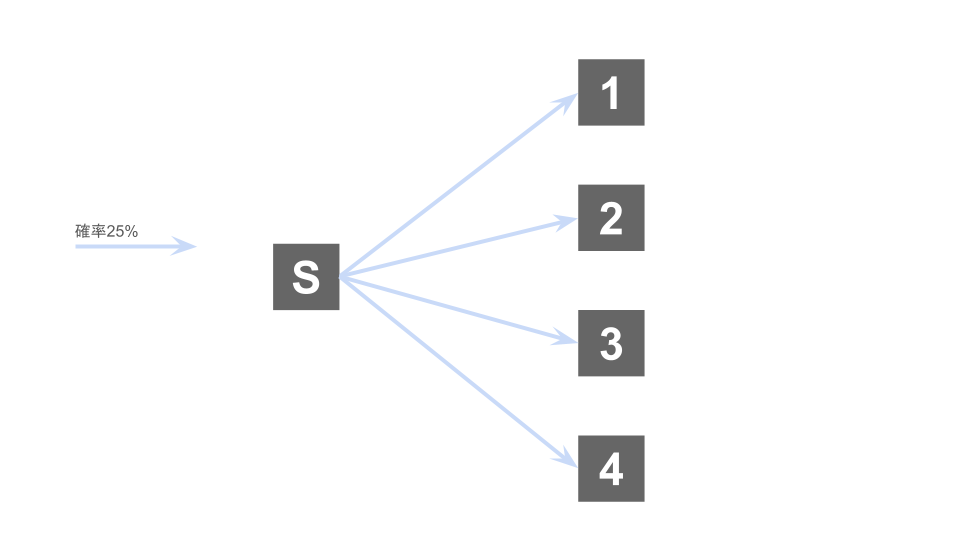
試行2回目で初めて箱1を選ぶ確率
試行2回目で初めて箱1を選ぶ確率は、’普通の’ネズミと同様に$\frac34\times\frac13 = \frac14$である。
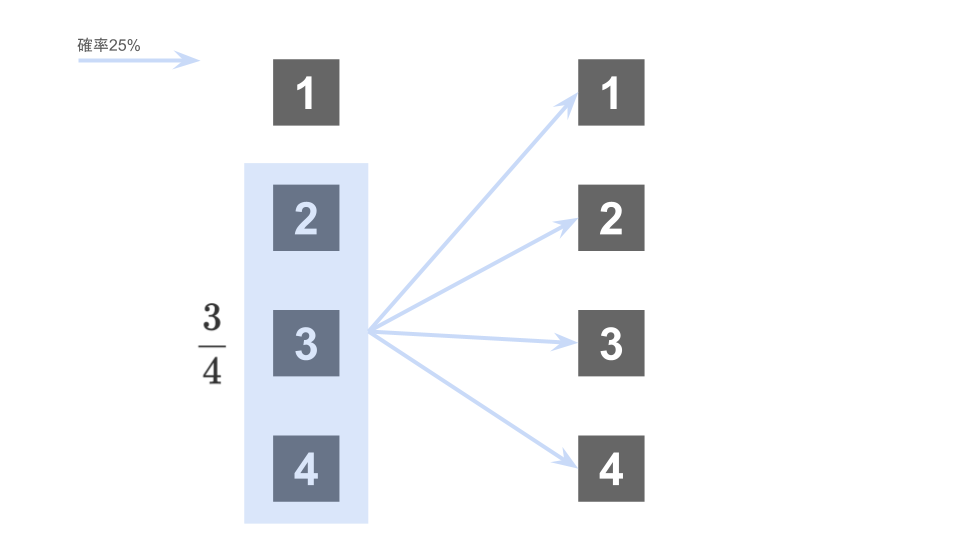
試行3回目で初めて箱1を選ぶ確率
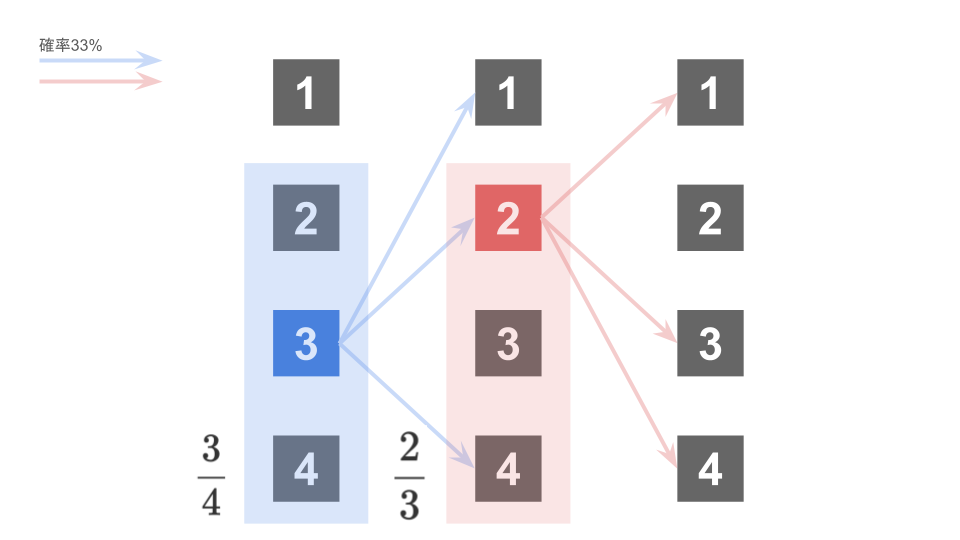
試行3回目以降が’利口な’ネズミが他のネズミと異なるポイントである。
以下の図のように、試行1回目で箱3、試行2回目で箱2を選んだとすると、’利口な’ネズミは試行3回目では箱2,3は選ばず、箱1,4のどちらかを選ぶこととなる。
つまり、試行3回目で初めて箱1を選ぶ確率は以下のように求めることができる。
$$\frac34 \times \frac23 \times \frac12 = \frac14$$
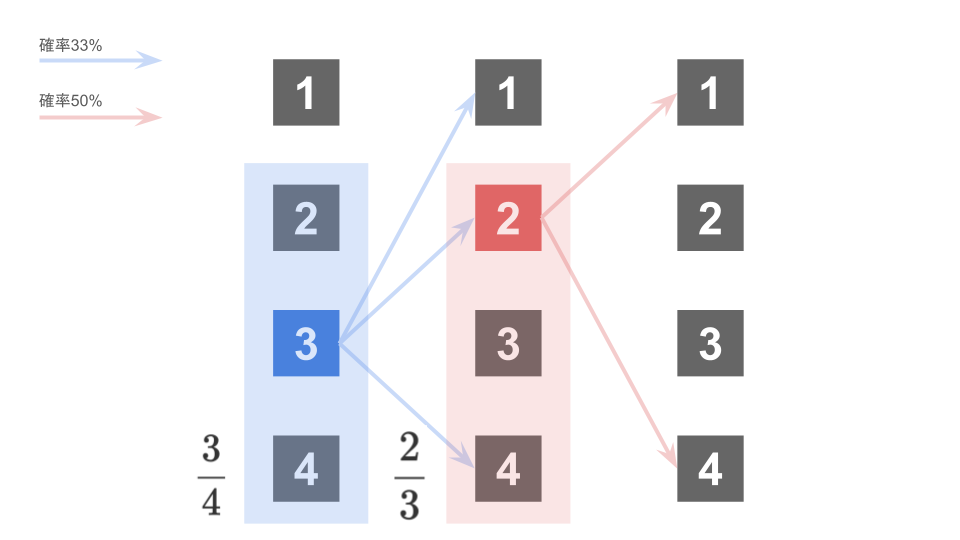
試行4回目で初めて箱1を選ぶ確率
試行4回目では’利口な’ネズミは必ず食物の入った箱1を選ぶことができる。
なぜなら、過去3回で他の箱3つの中に食物がないことを知っているからだ。
よって、試行4回目で初めて箱1を選ぶ確率は以下のように計算することができる。
$$\frac34 \times \frac23 \times \frac12 \times 1 = \frac14$$
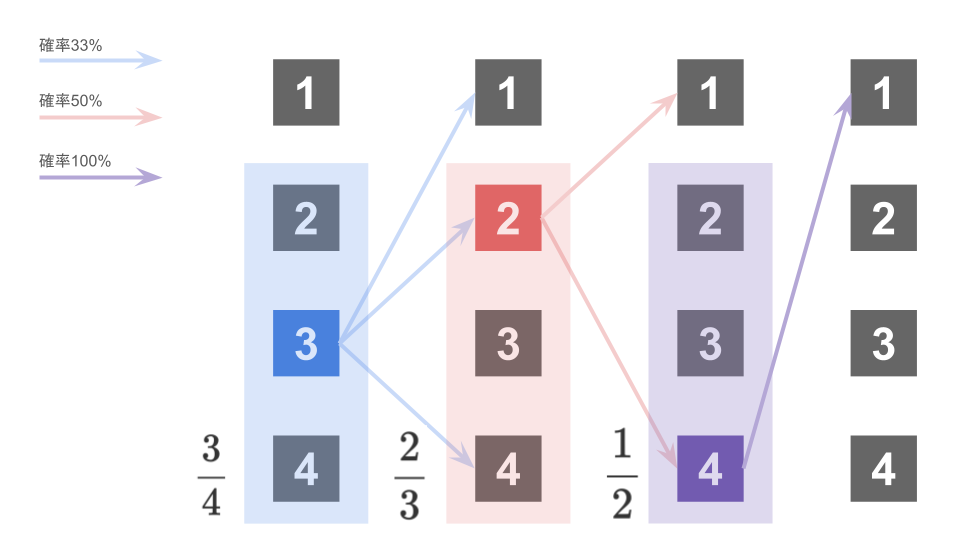
よって、すべての試行において、’利口な’ネズミが箱1を選ぶ確率は$\frac14$であることがわかる。
試行回数の期待値を計算
ここまで求めてきた確率を使って、試行回数の期待値$E(X)$を求めると
$$E(X) = \sum_{n = 1}^4 \frac{n}{4} = \frac14 \sum_{n = 1}^4 n = \frac14 \times \frac12 \times 4 \times(4+1) = \frac52$$
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第10章-演習問題3「行動科学的モデル」について丁寧に解説してみました!
結論としては、ネズミが利口になればなるほど試行回数の期待値は減少する、ということがお分かりいただけたかと思います。($4 > 3.25 > 2.5$)
単純な推移確率の場合は上記のように数列の一般項を求めることによって期待値を計算することができるので、ぜひ覚えておいてください!



コメント