今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題5「対称性の符号検定」をPythonで解いていきたいと思います。
今回の問題の主題は「分布は平均0で対称か?」という問題になります。
データを平均で引き算してあげればどのような分布に対しても、解説の方法で対称性の検証は可能ですので、ぜひ活用してみてください!
問題文
<対称性の符号検定>
次のデータが対称な分布から得られたものとして、符号検定を用いて、平均が$0$であるという仮説を有意水準5%で両側検定せよ。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章 演習問題 P229
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
符号検定とは?
符号検定とは、ノンパラメトリック検定と呼ばれる分布の仮定によらない検定のうち、分布が対称であるならば$\theta = 0$が平均になることを利用して、分布の対称性を検定する方法になります。
符号検定の際には、以下3点を利用して仮説$\theta = 0$を検証します。
- 仮説$\theta = 0$が$p = \frac12$と同等になること
- $p = \frac12$より$N = \{X_1,\cdots,X_nのうち、X_i \geqq 0のものの個数\}$は二項分布$Bi(n,~p)$に従うこと
- 有意水準$\alpha$の時、$P(|N-n/2| \geqq c) = \alpha$となるような$c$を探索的に見つけることで、有意水準$\alpha$の検定方式が得られる
実装コード
本問題は以下のコードによって解いていきます。
コードは以下の2つに分かれています。
- $P(|N-n/2| \geqq c) = \alpha$を満たすような$c$を見つけるコード
- 上記で見つけた$c$を用いて、符号検定を行うコード
import numpy as np
import pandas as pd
import math
df = pd.read_csv('sign_test_of_symmetry.csv')
display(df)
n = len(df)
print(n)
for i in range(n + 1):
# 確率pの分母を計算(二項分布を仮定)
p_deno = 1/(2 ** n)
# 確率pの分子の初期値
p_num = 0
# iがnの半分より小さい場合はそのまま計算
if i < n/2:
for j in range(i + 1):
p_num += math.comb(n, j)
# iがnの半分以上の場合は組み合わせnCrの性質を利用して、n-iまでの組み合わせを計算
else:
for j in range(n- i + 1):
p_num += math.comb(n, j)
# 分母と分子をかけ算
p = p_deno * p_num
if i < n/2:
print(f'P(N<={i}) = {p}')
else:
print(f'P(N>={i}) = {p}')import numpy as np
import pandas as pd
import math
df = pd.read_csv('sign_test_of_symmetry.csv')
display(df)
plus_arr = []
for index, row in df.iterrows():
num = row['データ']
# 0より大きい数をカウント
if num > 0:
plus_arr.append(num)
N = len(plus_arr)
print(f'N = {N}')
# 先ほどのp値からP(N<=k)=0.25またはP(N>=k)=0.25となる点kを代入する
if N <= 4 or N >= 13:
print('有意水準5%で平均0という仮説は棄却される')
else:
print('有意水準5%で平均0という仮説は棄却されない')コード1解説
「$P(|N-n/2| \geqq c) = \alpha$を満たすような$c$を見つけるコード」は以下のような手順で$c$を導出しています。
- $P(N \leqq k)$または$P(N \geqq k)$の分母の値を求める
- $P(N \leqq k)$または$P(N \geqq k)$の分子の値を、$k$が$\frac{n}2$より大きいか小さいかで場合分けをして求める
- 先ほど求めた分母と分子をかけ算して、$P(N \leqq k)$または$P(N \geqq k)$の値を求める
上記手順を順を追って解説をしていく前に、コードを実装する際の前提について確認をしていきましょう。
$P(|N-n/2| \geqq c) = \alpha$を求めるために、$P(N \leqq k)$または$P(N \geqq k)$を計算する理由
$P(|N-n/2| \geqq c) = \alpha$を式変形すると,
$$P(|N-n/2| \geqq c) = P(N – n/2 \leqq -c) + P(N – n/2 \geqq c)$$
$$= P(N \leqq n/2 -c) + P(N \geqq n/2 + c) = \alpha$$
よって、$P(N \leqq n/2 -c)$と$P(N \geqq n/2 + c)$が足して有意水準$\alpha$となるような$c$の値を探せば良い。
ここで、たとえばデータ数が$n = 17$である時、$P(N \leqq 3)$は以下のように計算される。
$$P(N \leqq 3) = \frac{({}_{17}\mathrm{C}_{0} +{}_{17}\mathrm{C}_{1} +{}_{17}\mathrm{C}_{2} +{}_{17}\mathrm{C}_{3})}{2^n}$$
ここで、${}_n\mathrm{C}_k = {}_n\mathrm{C}_{n-k}$であることと上式から
$$P(N \geqq 14) = \frac{({}_{17}\mathrm{C}_{17} +{}_{17}\mathrm{C}_{16} +{}_{17}\mathrm{C}_{15} +{}_{17}\mathrm{C}_{14})}{2^n} $$
$$= \frac{({}_{17}\mathrm{C}_{0} +{}_{17}\mathrm{C}_{1} +{}_{17}\mathrm{C}_{2} +{}_{17}\mathrm{C}_{3})}{2^n} = P(N \leqq 3)$$
また、$14 = \frac{17}2 + 5.5$、$3 = \frac{17}2 – 5.5$であることから、
$$P(N \leqq n/2 -c) = P(N \geqq n/2 + c)$$
であるし、
$$P(N \leqq k) = P(N \geqq n-k)$$
である。
よって、$P(|N-n/2| \geqq c) = \alpha$を満たす$c$を見つけることと、$P(N \leqq k) = \alpha /2$または$P(N \geqq k) = \alpha /2$を満たす$k$を見つけることは同じことである。
$P(N \leqq k)$または$P(N \geqq k)$の分母の値を求める
df = pd.read_csv('sign_test_of_symmetry.csv')
display(df)
n = len(df)
print(n)
for i in range(n + 1):
# 確率pの分母を計算(二項分布を仮定)
p_deno = 1/(2 ** n)$k < n/2$の時、$P(N \leqq k)$の確率は以下のように式変形できる。
$$P(N \leqq k) = \sum_{j = 0}^k {}_n\mathrm{C}_{j} \left(\frac12\right)^j\left(\frac12\right)^{n-j} = \sum_{j = 0}^k {}_n\mathrm{C}_{j} \left(\frac12\right)^n = \frac{\sum_{j = 0}^k {}_n\mathrm{C}_{j}}{2^n}$$
そのため、コード内ではまず先にp_denoとして分母の$2^n$部分を計算している
$P(N \leqq k)$または$P(N \geqq k)$の分子の値を、$k$が$\frac{n}2$より大きいか小さいかで場合分けをして求める
# 確率pの分子の初期値
p_num = 0
# iがnの半分より小さい場合はそのまま計算
if i < n/2:
for j in range(i + 1):
p_num += math.comb(n, j)
# iがnの半分以上の場合は組み合わせnCrの性質を利用して、n-iまでの組み合わせを計算
else:
for j in range(n- i + 1):
p_num += math.comb(n, j)$k < n/2$の時は、
$$P(N \leqq k) = \frac{\sum_{j = 0}^k {}_n\mathrm{C}_{j}}{2^n}$$
と計算されるので、上記コードで前半部分で0から$k$までの組み合わせの和を計算している
$k \geqq n/2$の時は、${}_n\mathrm{C}_k = {}_n\mathrm{C}_{n-k}$であることを利用して、
上記コードで前半部分で0から$n-k$までの組み合わせの和を計算している
先ほど求めた分母と分子をかけ算して、$P(N \leqq k)$または$P(N \geqq k)$の値を求める
# 分母と分子をかけ算
p = p_deno * p_num
if i < n/2:
print(f'P(N<={i}) = {p}')
else:
print(f'P(N>={i}) = {p}')先ほどまでに計算した分母と分子をかけ算し、$k$が$n/2$未満か以上かに応じた出力を行う。
これによって、$P(N \leqq k)$または$P(N \geqq k)$の確率を求めることができ、それらの値が$\alpha /2$のような$k$を見つけ出すことができる。

出力結果より、$P(N \leqq k)=\alpha/2$または$P(N \geqq k)=\alpha/2$となる$k$の値は4または13であることがわかる。
コード2解説
上記で見つけた$c$改め$k$を用いて、符号検定を行うコードは以下の2ステップで実行する。
- 全てのデータのうち、0より大きいデータの数をカウントする
- カウントしたデータ数と先ほど求めた$k$の値とを比較する
順を追って解説していきます。
全てのデータのうち、0より大きいデータの数をカウントする
plus_arr = []
for index, row in df.iterrows():
num = row['データ']
# 0より大きい数をカウント
if num > 0:
plus_arr.append(num)
N = len(plus_arr)
print(f'N = {N}')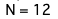
符号検定は平均$\theta = 0$を仮定しているため、0以上または0以下のデータ数の偏りは仮定に反します。
そのため、0以上のデータ数をカウントすることによって、その後の検定のための準備を行います。
今回のデータでは0より大きいデータが12個あるということがわかりました。
カウントしたデータ数と先ほど求めた$k$の値とを比較する
# 先ほどのp値からP(N<=k)=0.25またはP(N>=k)=0.25となる点kを代入する
if N <= 4 or N >= 13:
print('有意水準5%で平均0という仮説は棄却される')
else:
print('有意水準5%で平均0という仮説は棄却されない')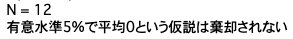
コード1で求めた$k=4,13$を使用して、0より大きいデータ数が多すぎないか、少な過ぎないかを検証します。
今回のデータ数においては有意水準5%で14個以上0より大きいデータがないと統計的に優位とは言えないので、平均0という仮説は棄却されない結果となりました。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題5「対称性の符号検定」をPythonで解いていきました。
平均0であることから二項分布が利用できることがわかってしまえば、0以上のデータの個数をカウントすることによって、データの偏りを検定することができる、というのが本問題の解法でした。
皆さんも分布の対称性を検定する場合には本記事の内容を参考にしてみてください!





コメント