
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題4「極座標法」について丁寧に解説をしていきたいと思います!
逆関数の微分や偏微分などの高校数学の復習にもなりますので、数学問題のコテならしにぜひ取り組んでみてください!
問題文
<極座標法>
正規乱数を発生するための極座標法(11.6)が正しいことを、次の方針に従って確かめよ.
確率変数の組$(U_1, U_2)$の密度関数を$f(u_1, u_2)$、$(X_1, X_2)$の密度関数を$g(x_1, x_2)$とすると、
$$g(x_1, x_2) = |J|\cdot f(u_1, u_2)$$
が成り立つ。
ただし、$|J|$はヤコビ行列式(ヤコビアン)
$$J = \frac{\partial (u_1, u_2)}{\partial (x_1, x_2)}$$
の絶対値である
※(11.6)
$$ X_1 = \sqrt{-2\log U_1} \cos(2\pi U_2)$$
$$ X_2 = \sqrt{-2\log U_1} \sin(2\pi U_2)$$
なお、$U_1, U_2$は一様乱数であり、$X_1, X_2$が互いに標準正規分布$N(0, 1)$に従うことを証明することが今回の演習のゴールである
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第11章 P331~332
解説
本問題は以下の3ステップで解いていきます。
- 式変形をして、$u_1, u_2$を求める
- $u_1, u_2$を$x_1, x_2$でそれぞれ偏微分する
- ヤコビ行列式を計算する
- $|J|\cdot f(u_1, u_2)$を計算する
順を追って解説していきます.
式変形をして、$u_1, u_2$を求める
確率変数の実現値
$$ x_1 = \sqrt{-2\log u_1} \cos(2\pi u_2) \cdots (1)$$
$$ x_2 = \sqrt{-2\log u_1} \sin(2\pi u_2) \cdots (2)$$
について考える。
(1)式と(2)式を2乗して合計すると
$$x_1^2 + x_2^2 = -2\log u_1(\cos^2 (2\pi u_2) + \sin^2 (2\pi u_2)) = -2\log u_1$$
$$2\log u_1 = – (x_1^2 + x_2^2)$$
$$u_1 = e^{- \frac{x_1^2 + x_2^2}2} \cdots (*)$$
$(*)$式を(1)式に代入すると、
$$x_1 = \sqrt{x_1^2 + x_2^2} \cos(2 \pi u_2)$$
$$\cos(2 \pi u_2) = \frac{x_1}{\sqrt{x_1^2 + x_2^2}}$$
ここで、上式を図示すると以下のようになる。
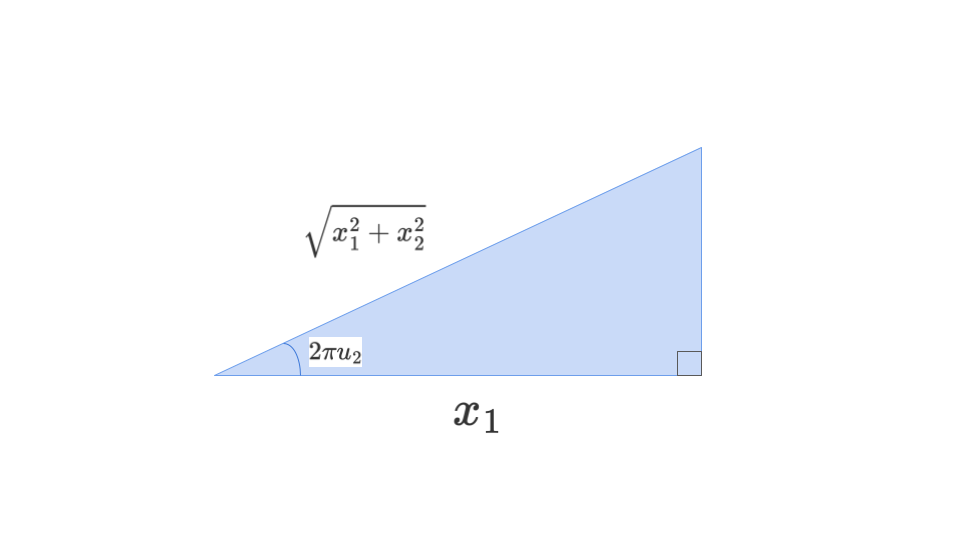
※分かり易さのために直角三角形で書いていますが、実際には$0 \leqq u_2 \leqq 1$より$0 \leqq 2\pi u_2 \leqq 2\pi$であることから、上記関係図は本来的には座標として表現した方が正しいです。
ここで、三平方の定理より、上図の縦の辺の長さが$x_2$であることがわかります。
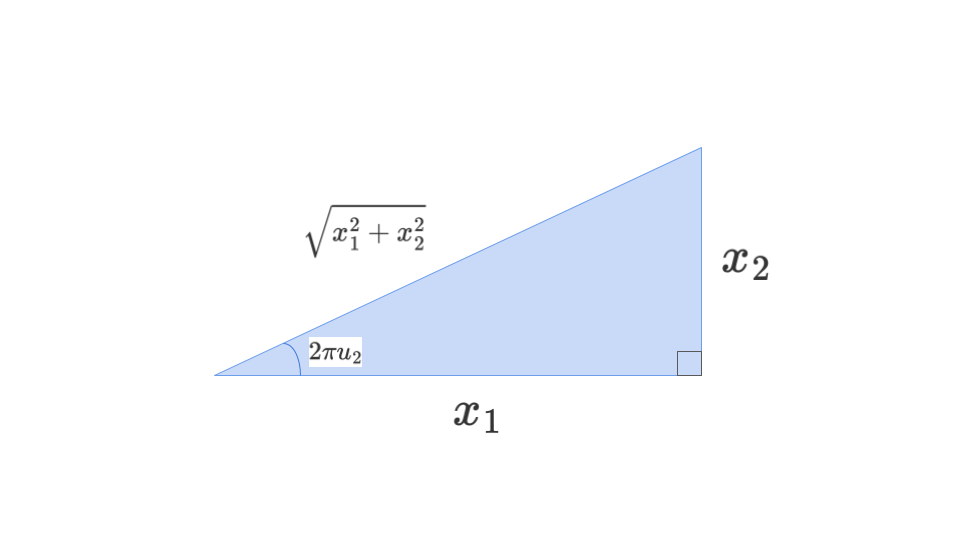
ここで、上図から以下のような式が成り立つことが分かります。
$$\tan(2\pi u_2) = \frac{x_2}{x_1}$$
$$2 \pi u_2 = \tan^{-1}\left( \frac{x_2}{x_1}\right)$$
$$u_2 = \frac{1}{2\pi}\tan^{-1}\left( \frac{x_2}{x_1}\right)$$
よって、ここまでの計算の結果をまとめると、
$$u_1 = e^{- \frac{x_1^2 + x_2^2}2}$$
$$u_2 = \frac{1}{2\pi}\tan^{-1}\left( \frac{x_2}{x_1}\right)$$
$u_1, u_2$を$x_1, x_2$でそれぞれ偏微分する
$u_1$を$x_1, x_2$でそれぞれ偏微分すると、
$$\frac{\partial u_1}{\partial x_1} = -x_1 \cdot e^{- \frac{x_1^2 + x_2^2}2} = -x_1 u_1$$
$$\frac{\partial u_1}{\partial x_2} = -x_2 \cdot e^{- \frac{x_1^2 + x_2^2}2}= -x_2 u_1$$
$u_1$を$x_1, x_2$でそれぞれ偏微分する前に、$\tan^{-1}x$の微分について考える。
$y = \tan^{-1}x$とすると、$x = \tan y$であることから
$$ \frac{dy}{dx} = \frac1{\frac{dx}{dy}} = \frac1{\frac1{\cos^2 y}}$$
ここで、三角関数の性質から
$$1 + \tan^2 y = \frac1{\cos^2 y}$$
よって、
$$\frac{dy}{dx} = \frac1{1 + \tan^2 y } = \frac1{1 + x^2}$$
これを利用して$u_2$の$x_1$での偏微分を考えると
$$\frac{\partial u_2}{\partial x_1} = \frac1{2\pi} \cdot \left( -\frac{x_2}{x_1^2}\right)\cdot \frac1{1 + \left(\frac{x_2}{x_1}\right)^2}$$
$$ = \frac1{2\pi} \cdot \frac{- x_2}{x_1^2 + x_2^2}$$
同様にして、$u_2$の$x_2$での偏微分を考えると
$$\frac{\partial u_2}{\partial x_2} = \frac1{2\pi} \cdot \left( \frac1{x_1}\right)\cdot \frac1{1 + \left(\frac{x_2}{x_1}\right)^2}$$
$$ = \frac1{2\pi} \cdot \left( \frac{x_1}{x_1^2}\right)\cdot \frac1{1 + \left(\frac{x_2}{x_1}\right)^2}$$
$$ = \frac1{2\pi} \cdot \frac{x_1}{x_1^2 + x_2^2}$$
ヤコビ行列式を計算する
先ほどまでの計算結果を使ってヤコビ行列を計算すると、
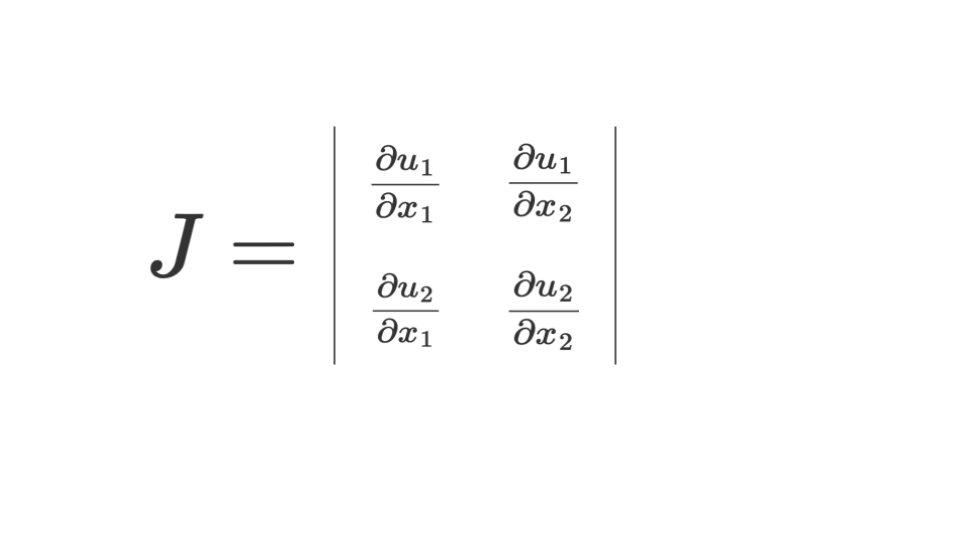
$$ = \frac{\partial u_1}{\partial x_1} \cdot \frac{\partial u_2}{\partial x_2} – \frac{\partial u_1}{\partial x_2}\cdot \frac{\partial u_2}{\partial x_1}$$
$$ = \frac1{2\pi}\cdot \frac1{x_1^2 + x_2^2}\left( – x_1 u_1\times x_1 – (- x_2 u_1) \times (- x_2)\right)$$
$$= \frac1{2\pi}\cdot \frac1{x_1^2 + x_2^2}\left( -u_1(x_1^2 + x_2^2) \right) = \frac{-u_1}{2\pi}$$
$$ = \frac{-1}{2\pi}\exp\left(\frac{x_1^2 + x_2^2}{2}\right)$$
$$ = – \frac1{\sqrt{2\pi}}\exp\left(-\frac{x_1^2}2\right) \times \frac1{\sqrt{2\pi}}\exp\left(-\frac{x_2^2}2\right)$$
よって、絶対値を取ると、
$$|J| = \frac1{\sqrt{2\pi}}\exp\left(-\frac{x_1^2}2\right) \times \frac1{\sqrt{2\pi}}\exp\left(-\frac{x_2^2}2\right)$$
$|J|\cdot f(u_1, u_2)$を計算する
ここで、$u_1, u_2$は一様乱数であるから
$$f(u_1, u_2) = 1~~(0 \leqq u_1 \leqq 1, ~ 0 \leqq u_2 \leqq 1)$$
これは
$$\int_{-\infty}^\infty \int_{-\infty}^\infty f(u_1, u_2) du_1 du_2 = \int_{0}^1 \int_0^1 f(u_1, u_2) du_1 du_2 = 1$$であることから確かめられる。
よって、$g(x_1, x_2)$について
$$g(x_1, x_2) = |J|f(u_1, u_2) = \frac1{\sqrt{2\pi}}\exp\left(-\frac{x_1^2}2\right) \times \frac1{\sqrt{2\pi}}\exp\left(-\frac{x_2^2}2\right)$$
これは、確率変数$X_1, X_2$が互いに独立で、標準正規分布に従うことを表す。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題4「極座標法」について丁寧に解説していきました!
$x_1, x_2$から$u_1, u_2$の式を導出する過程は少しテクニックが必要だと感じたのではないでしょうか?
本記事の解説が皆さんの独学の助けとなれば幸いです!



コメント