
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題4「幹葉表示とロバスト推定」をPythonで解いていきたいと思います。
外れ値や分布に偏りがあるような時に、どれだけ尤もらしい推定量を求めるかについて扱っている問題/解説になりますので、ご参考にしていただけると幸いです!
問題文
<幹葉表示とロバスト推定>
下のデータはプラスチック製品の成型工程で製品の肉厚(mm)を測定したものである。
i ) このデータを幹葉表示せよ
ii ) 標本平均$\bar{X}$を求めよ
iii ) 標本中央値$X_{med}$を求めよ
iv ) $k=3$のトリム平均$\hat{\theta}_{trim}(3)$を求めよ
v ) フーバー型推定量$\hat{\theta}_{H}$の値を求めよ
vi ) 以上の推定量を比較して考察せよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章 演習問題 P229
トリム平均とは?
トリム平均とは、総数$n$のデータのうち、大きい方と小さい方からそれぞれ$k$個のデータを取り除き、残りの$n-2k$個の平均のことを指します。
$$\hat{\theta}_{trim}(k) = \frac1{n-2k}(X_{(k+1)} + \cdots + X_{(n-k)})$$
トリム平均は、データに外れ値が見込まれる場合にその影響を受けない頑強な(=ロバストな)指標として使われています。
フーバー型推定量とは?
フーバー型推定量は、ざっくりいうと標本中央値をベースで考えつつも、少し分布の偏りを考慮するような推定量のことです。
フーバー型推定量導出の手順は以下の4ステップです。
- データ数$n$の約4分の1の個数$s$を求める
- データの四分位範囲$d$とその半分$c$を計算する
- 中央値から上下に$c$だけ離れた範囲にある数字の個数$m$と合計$S$を計算する
- 中央値から上下に$c$だけ離れた範囲から上下に外れたデータの数$m_L,~m_U$をそれぞれ計算する
- ここまでに計算した$S,~c,~m_U,~m_L,~m$を使ってフーバー型推定量を求める
なお、それぞれの値の計算式は以下のようになります。
$$s = \frac{([n/2] + 1)]2$$
$$d = X_{(n-s+1)} – X_{(s)}$$
※$s$が小数の場合は$X_{(s)} = \frac{X_{(s-0.5)} + X_{(s + 0.5)}}2$とする
$$m = ([X_{med}-c,~X_{med} + c])の範囲にある観測値の個数$$
$$S = ([X_{med}-c,~X_{med} + c])の範囲にある観測値の合計$$
$$m_L = X_{med}-cより小さい観測値の個数$$
$$m_U = X_{med}-cより大きい観測値の個数$$
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
実装コード
本問題を解くPythonコードは以下のようになります。
import numpy as np
import pandas as pd
import math
# データの読み込みと配列化
df = pd.read_csv('Stem_leaf_display_and_robust_estimation.csv')
arr = df['プラスチック製品の肉厚']
#1
num_df = pd.DataFrame(index = np.arange(4.6, 5.7, 0.1), columns = ['stem'])
for a in arr:
a = str(a)
# 小数第1位までと小数第2位までを分離
a, b = a[:3], a[-1]
for index,row in num_df.iterrows():
# 全てのnanを空文字にしておく
if str((num_df.at[index, 'stem'])) == 'nan':
num_df.at[index, 'stem'] = ''
# インデックスとa(=小数第2位まで)の誤差が0.001以下だったときに、b(=小数第3位)を幹葉表示に追加する
if np.abs(float(index) - float(a)) < 0.001:
num_df.at[index, 'stem'] = str(num_df.at[index, 'stem']) + str(b)
display(num_df)
#2
mean = np.mean(arr)
print(f'平均: {mean}')
#3
med = np.median(arr)
print(f'中央値: {med}')
#4
k = 3
sort_arr = sorted(arr)
# ソートした結果から上位・下位3データを取り除く
trim_arr = sort_arr[k:-k]
trim_m = np.mean(trim_arr)
print(f'トリム平均: {trim_m}')
#5
n = len(arr)
# 4分の1のデータ数を計算
s = (math.floor(n / 2) + 1)/2
# sに端数が出る時
if math.floor(n / 2) % 2 == 0:
s = int(math.floor(n / 2)/2)
x_ns1 = (sort_arr[n - s -1] + sort_arr[n - s]) /2
xs = (sort_arr[s-1] + sort_arr[s]) / 2
# sに端数が出ない時
else:
x_ns1 = sort_arr[n - s]
xs = sort_arr[s-1]
# 四分位範囲の計算
d = x_ns1 - xs
c = d/2
lower = med - c
upper = med + c
m = 0
mu = 0
ml = 0
S = 0
for num in arr:
# mLのカウント
if num < lower:
ml += 1
# mのカウントとSの加算
elif num < upper:
m += 1
S += num
# mUのカウント
else:
mu += 1
thetah = (S + c * (mu - ml)) / m
print(f'フーバー型推定量: {thetah}')
解説
上記コードについて順を追って解説していきます。
幹葉表示の作成
#1
num_df = pd.DataFrame(index = np.arange(4.6, 5.7, 0.1), columns = ['stem'])
for a in arr:
a = str(a)
# 小数第1位までと小数第2位までを分離
a, b = a[:3], a[-1]
for index,row in num_df.iterrows():
# 全てのnanを空文字にしておく
if str((num_df.at[index, 'stem'])) == 'nan':
num_df.at[index, 'stem'] = ''
# インデックスとa(=小数第2位まで)の誤差が0.001以下だったときに、b(=小数第3位)を幹葉表示に追加する
if np.abs(float(index) - float(a)) < 0.001:
num_df.at[index, 'stem'] = str(num_df.at[index, 'stem']) + str(b)
display(num_df)
上記コードでは、以下の4手順で幹葉表示を完成させています。
- データの上限と下限をカバーするようなデータフレームnum_dfを作成
- データから小数第1位までの値aと小数第3位だけの値bを抽出
例: 4.62 → $a =4.6, ~ b = 2$ - aとデータフレームのインデックスを比較し、随時bを追加する
※差分が0.0001以下の時、としているのはインデックスを浮動小数点(=float)に戻す時に0.0000001単位での誤差が生じるため
例: インデックス4.7を浮動小数点に → 4.69999999
標本平均・標本中央値の導出
#2
mean = np.mean(arr)
print(f'平均: {mean}')
#3
med = np.median(arr)
print(f'中央値: {med}')
トリム平均の導出
#4
k = 3
sort_arr = sorted(arr)
# ソートした結果から上位・下位3データを取り除く
trim_arr = sort_arr[k:-k]
trim_m = np.mean(trim_arr)
print(f'トリム平均: {trim_m}')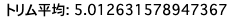
フーバー型推定量の導出
#5
n = len(arr)
# 4分の1のデータ数を計算
s = (math.floor(n / 2) + 1)/2
# sに端数が出る時
if math.floor(n / 2) % 2 == 0:
s = int(math.floor(n / 2)/2)
x_ns1 = (sort_arr[n - s -1] + sort_arr[n - s]) /2
xs = (sort_arr[s-1] + sort_arr[s]) / 2
# sに端数が出ない時
else:
x_ns1 = sort_arr[n - s]
xs = sort_arr[s-1]
# 四分位範囲の計算
d = x_ns1 - xs
c = d/2
lower = med - c
upper = med + c
m = 0
mu = 0
ml = 0
S = 0
for num in arr:
# mLのカウント
if num < lower:
ml += 1
# mのカウントとSの加算
elif num < upper:
m += 1
S += num
# mUのカウント
else:
mu += 1
thetah = (S + c * (mu - ml)) / m
print(f'フーバー型推定量: {thetah}')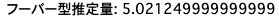
上記コードにおいては、上記✔︎CHECK記載の手順でフーバー推定量を求めています。
- データ数$n$の約4分の1の個数$s$を求める
- データの四分位範囲$d$とその半分$c$を計算する
- 中央値から上下に$c$だけ離れた範囲にある数字の個数$m$と合計$S$を計算する
- 中央値から上下に$c$だけ離れた範囲から上下に外れたデータの数$m_L,~m_U$をそれぞれ計算する
- ここまでに計算した$S,~c,~m_U,~m_L,~m$を使ってフーバー型推定量を求める
順を追って解説いたします。
データ数$n$の約4分の1の個数$s$を求める
n = len(arr)
# 4分の1のデータ数を計算
s = (math.floor(n / 2) + 1)/2math.floorは()内の数字を超えないような最大の整数を返す関数です。
例えば、math.floor(16.5)と入力すると、16が返ってきます。
データの四分位範囲$d$とその半分$c$を計算する
# sに端数が出る時
if math.floor(n / 2) % 2 == 0:
s = int(math.floor(n / 2)/2)
x_ns1 = (sort_arr[n - s -1] + sort_arr[n - s]) /2
xs = (sort_arr[s-1] + sort_arr[s]) / 2
# sに端数が出ない時
else:
x_ns1 = sort_arr[n - s]
xs = sort_arr[s-1]
# 四分位範囲の計算
d = x_ns1 - xs
c = d/2上記コードには2点ほど注意が必要です。
- 配列sort_arrにおいては左から$s$番目の数字を求めたい場合は、配列の最初のインデックスは0であるため、sort_arr[s-1]のように指定する
- sに端数が出る場合と出ない場合とで計算方法が異なる
中央値から上下に$c$だけ離れた範囲にある数字の個数$m$と合計$S$を計算する & 中央値から上下に$c$だけ離れた範囲から上下に外れたデータの数$m_L,~m_U$をそれぞれ計算する
lower = med - c
upper = med + c
m = 0
mu = 0
ml = 0
S = 0
for num in arr:
# mLのカウント
if num < lower:
ml += 1
# mのカウントとSの加算
elif num < upper:
m += 1
S += num
# mUのカウント
else:
mu += 1配列内の数字を$X_{med} – c$より小さいもの、$X_{med} + c$より小さいもの、$X_{med} + c$より大きいものの順に評価することによって、$m,~m_L,~m_U,~S$を求めています。
ここまでに計算した$S,~c,~m_U,~m_L,~m$を使ってフーバー型推定量を求める
thetah = (S + c * (mu - ml)) / m
print(f'フーバー型推定量: {thetah}')考察

上記幹葉表示を見ると、5.57付近に外れ値が見られることが分かります。
よって、データの分布としては上に裾が長い形となり、平均値は中央値より少し外れ値に影響を受けたような値になっています。
そこで$k=3$のトリム平均$\hat{\theta}_{trim}(3)$を求めると、標本平均よりも0.015ほど低い値が算出されました。
一方で、$k=3$のトリム平均では外れ値とは言えない5.25の値も取り除いてしまっているため、中央値よりも0.07ほど小さな値が算出されています。
$k$の値としては、$n$が小さければ$1$か$2$くらい、$n$がある程度大きければ$n$の5%か10%とするのが普通
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章 P212
とありますので、少しデータを消去し過ぎているかもしれません。
フーバー型推定量については、標本中央値より0.0012ほど上方修正された値となっており、下裾を考慮し過ぎず、5.57という外れ値の影響も除去している点で、尤もらしい推定量と言えるのではないでしょうか。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題4「幹葉表示とロバスト推定」をPythonで解いていきました。
分布に偏りのあるような場合には外れ値をどのように扱うか、というのが推定量を求める上で考慮すべき事項として上がってきます。
そのような時に平均値、中央値、最頻値以外の推定量を使い分けられると、分布の検証結果の妥当性が増すものと思われますので、ぜひ推定量の引き出しとして頭の片隅に置いていただけると幸いです。




コメント