
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題6「統計的決定理論」について丁寧に解説していきたいと思います。
この問題を通して、取りうる選択のコストを元に、「ある行動がベストな選択であるのは、事前確率がどのような範囲にある時か」という範囲を求めることができるようになります。
問題文
<統計的決定理論>
ネルソン氏の状況(下表1)において、
表1 i ) 晴天$\theta_1$、雨天$\theta_2$の事前確率が$1/2, 1/2$の時、ネルソン氏にとって$a_1, a_2, a_3$のどの行動が最適か.
一般に、事前確率が$w, 1-w$の時はどうか.
$w$の範囲で分類して答えよ.
また、晴天用で外出する時の$w$の範囲を求めよ.(ノー・データ問題)
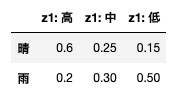
ii ) 晴雨計の示度のデータがあるとして、示度が$z_i (i = 1,2,3)$の時、下表2から晴天$\theta_1$、雨天$\theta_2$の事後確率を各$z_i$に対して求めよ
表2 iii ) (i)の事後確率$w, 1-w$を(ii)で求めた事後確率に代えて、$a_1, a_2, a_3$の中からネルソン氏の最適行動を求めよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第9章 演習問題 P274
ノー・データ問題とは?
本問題の(i)のように、事前確率として$w, 1-w$のような何の情報もないような仮定に対して、具体的なデータを得るよりも先に
$$\sum w_i L(\theta_i, a_i) \cdots (*)$$
を最小化する行動・選択$a^* = a_j$をあらかじめ求めておき、後から具体的なデータ(事後確率)$w'(\theta_1 | z_i)$を当てはめる方法がある。
この時、無情報の状態で$(*)$式を最小化することをノー・データ問題という。
ここで、$L(\theta, a)$は損失関数、つまり特定の状況下でその選択・行動をとった時のコストであり、問題文中の以下表の具体的な数字を表す。
例えば、雨の日に晴れ用の服で外出するとびしょ濡れになってコストが高いし、晴れの日にレインコート・レインシューズ・傘の完全防備で外出するのは動きづらいし暑くてコストがそこそこ高い。

事後確率の計算方法
母数$\theta$が離散的である時、$z$を標本のデータ、尤度関数を$f(z|\theta_i)$、事前確率を$w(\theta_i)$とすると、事後確率$w'(\theta_i | z)$は次のような式で得られる。
$$w'(\theta_i | z) = \frac{w(\theta_i) \cdot f(z|\theta_i)}{\sum w(\theta_i) \cdot f(z|\theta_i)}$$
(i)の解説
上記Checkより、与えられている情報が事前確率$w, 1-w$しかない状況下においては、以下式を最小にするような$a^* = a_j$を考える必要がある。
$$\sum w_i L(\theta_i, a_i) \cdots (*)$$
この時、行動$a_1, a_2, a_3$を選択した時の合計コストをそれぞれ$wL_1, wL_2, wL_3$とすると、表1を使って以下のように計算できる.
$$wL_1 = 0 \times w + 5 \times (1-w) = 5 – 5w$$
$$wL_2 = 1 \times w + 3 \times (1-w) = 3 – 2w$$
$$wL_3 = 3 \times w + 2 \times (1-w) = 2 + w$$
よって、最適な行動が$a_1$であるようなとき、合計コスト$wL_1$は他の行動のコストよりも小さくなるはずなので、以下の連立方程式を解けば、最適行動が$a_1$である時の$w$の範囲が求められる。
ここで、$w$は確率であるから、$0 \leqq w \leqq 1$であることに注意が必要である。
$$5-5w \leqq 3 – 2w$$
$$5-5w \leqq 2 + w$$
上記連立方程式を解くと、行動$a_1$が最適であるときの$w$の範囲は$\frac23 \leqq w \leqq 1$であると求められる。
同様にして、最適行動が$a_2$であるような$w$の範囲は、以下連立方程式を解くことによって求められる。
$$5 – 5w > 3-2w$$
$$3-2w < 2 + w$$
上記連立方程式を解くと、行動$a_2$が最適であるときの$w$の範囲は$\frac13 < w < \frac23$であると求められる。
よって、行動$a_3$が最適であるときの$w$の範囲は$0 \leqq w \leqq \frac13$であると求められる。
ここで、問題文にあるように、晴天$\theta_1$であるような事前確率が$w = \frac12$の時に、不等式が成立するのは$\frac13 < w < \frac23$であるから、晴天の事前確率が$w = \frac12$の時の最適行動は$a_2$であることがわかる。
問題文にある、「晴天用で外出するべきときの$w$の範囲」も上記計算から言わずもがな、$\frac23 \leqq w \leqq 1$である。
つまりは降水確率が34%以下の場合には晴れ用の服装で出掛けるべき、という判断になる。

(ii)の解説
天気の事前確率を$P(\theta_i)$、晴雨計の示す確率(尤度)を$P(z_i | \theta_i)$とすると、事後確率$P(\theta_1 | z_i)$は次のような式で計算することができる。
$$P(\theta_i | z_i) = \frac{P(\theta_i) \cdot P(z_i |\theta_i)}{\sum P(\theta_i) \cdot P(z|\theta_i)}$$
ここで、問題文より$P(\theta_1) = P(\theta_2) = \frac12$であるから、上式は以下のように簡単にすることができる
$$P(\theta_i | z_i) = \frac{\frac12 \cdot P(z_i |\theta_i)}{\sum \frac12 \cdot P(z|\theta_i)} = \frac{P(z_i |\theta_i)}{\sum P(z|\theta_i)}$$
よって、事後確率を尤度$z_1, z_2, z_3$ごとに計算すると次のようになる。
$$P(\theta_1 | z_1) = \frac{0.6}{0.6 + 0.2} = \frac34~~~~P(\theta_2 | z_1) = \frac14$$
$$P(\theta_1 | z_2) = \frac{0.25}{0.25 + 0.3} = \frac5{11}~~~~P(\theta_2 | z_2) = \frac6{11}$$
$$P(\theta_1 | z_3) = \frac{0.15}{0.15 + 0.5} = \frac3{13}~~~~P(\theta_2 | z_3) = \frac{10}{13}$$
(iii)の解説
(ii)より、
$$z_1の時の晴天\theta_1の事後確率P(\theta_1 | z_1) = \frac34$$
$$z_2の時の晴天\theta_1の事後確率P(\theta_1 | z_2) = \frac5{11}$$
$$z_3の時の晴天\theta_1の事後確率P(\theta_1 | z_3) = \frac3{13}$$
よって、ノー・データ問題(i)で求めた最適行動ごとの$w$の範囲と照らし合わせると、
$$z_1のとき、a_1が最適$$
$$z_2のとき、a_2が最適$$
$$z_3のとき、a_3が最適$$
ということがわかる。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題6「統計的決定理論」について丁寧に解説しました。
この問題、個別の事前確率$w, 1-w$を与えられた状態で
$$r = \sum_i w(\theta_i) \left{ \sum_j f(z_j | \theta_i) \cdot L(\theta_i, a^*(z_i))\right}$$
$r$を$a_1, a_2, a_3$ごとに求め、その中で$r$が最小になる$a_i$が最適な行動である、という求め方をすることもできます。
ですが、個別の$w$について考えるよりは一般的な$w$について最適行動の範囲を決めてから、具体的な$w$を入れて判断をする方が簡単であることが理解いただけたかと思います。
本記事を参考にノー・データ問題からの最適行動選択をぜひ社会実装していただけると幸いです!



コメント