「自然科学の統計学」第7章演習問題6-2標本問題と順位和検定をPythonで解いてみた

元教師

こんにちは！データサイエンティストの青木和也（https://twitter.com/kaizen_oni）です！

今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題6「2標本問題と順位和検定」をPythonで解いていきたいと思います。

こちらの問題は分布の仮定によらず、2つの標本が同一分布から抽出されたものであるかどうかを順位という尺度を使って検証する問題です。

2標本の分布を比較する際に使用する検定方法になりますので、ぜひ本記事を読んで理解された上で活用してみてください！

問題文
実装コード
解説
まとめ

問題文

＜2標本問題と順位和検定＞

2つの標本がある。

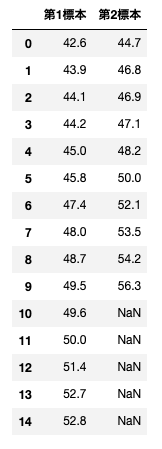
第1標本の標本の大きさは15で、その値を小さいものから順に並べると以下表のようになる。

第2標本の大きさは10で、その値は同じく以下表のようになる。

順位和検定により、2つの分布が等しいという仮説を有意水準5%で検定せよ。

東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章演習問題 P229

今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。

順位和検定とは？

順位和検定とは、2標本$X_1, \cdots, X_m, Y_1, \cdots, Y_n$の分布が等しいという仮説を、2標本を小さい順に並べた順番を利用して検定する検定方法です。

2標本を1から$M = m + n$まで一緒くたにして小さいものから順番に並べて、その中での$X_1, \cdots,X_m$の順位を$R_1,\cdots,R_m$とします。

$R_1,\cdots,R_m$の和$W$を順位和と呼びます。

$$W = \sum R_i$$

すると、仮説が正しい場合の$W$は

$$E(W) = \frac{m(M+1)}2,~~~V(W) = \frac{mn(M + 1)}{12}$$

の正規分布に従うことが知られているため、

$$\left|W – \frac{m(M + 1)}2\right| \geqq z_{\alpha/2}\sqrt{\frac{mn(M + 1)}{12}}$$

の時に仮説を棄却するというのが順位和検定の検定方法になります。

実装コード

本問題は以下のコードによって解くことができます。

import numpy as np
import pandas as pd
import math

df = pd.read_csv('two-sample_problem_and_rank-sum_test.csv')
display(df)
arr1 = df['第1標本']
arr2 = df['第2標本']

df1 = pd.DataFrame()
df1['sample'] = arr1
df1['flag'] = 1

df2 = pd.DataFrame()
df2['sample'] = arr2
df2['flag'] = 2
df2 = df2.dropna(how = 'any')

df = pd.concat([df1, df2], axis = 0)

df = df.sort_values('sample')
df = df.reset_index(drop = True)
display(df)

r_arr = []
for index, row in df.iterrows():
    num = index + 1
    flag = row.flag
    if flag == 1:
        r_arr.append(num)
    
m = len(df1)
n = len(df2)
M = m + n
W = np.sum(r_arr)
print(f'W = {W}')
print(f'm = {m}')
print(f'n = {n}')
print(f'M = {M}')

EW = m * (M  +1) /2
VW = m * n * (M + 1) / 12
s = math.sqrt(VW)
print(f'E(W) = {EW}')
print(f'V(W) = {VW}')
print(f's = {s}')

abs_w_ew = abs(W - EW)
print(f'|W- E(W)| = {abs_w_ew}')

z = 1.96 * s
print(f'z = {z}')

if abs_w_ew >= z:
    print(f'有意水準5%で母集団が等しいという仮説は棄却される')
else:
    print(f'有意水準5%で母集団が等しいという仮説は棄却されない')

解説

本問題は以下の5ステップによって解くことができます。

第1標本と第2標本を元々どちらの標本かという情報を保持したまま、1つのデータフレームに統合する
統合したデータフレームを値の小さい順に並び替える
第1標本の順位を配列に格納する
$m, n, M, W, E(W), V(W), 標準偏差sd$の値を求める
検定を行う

順を追って解説していきます。

第1標本と第2標本を元々どちらの標本かという情報を保持したまま、1つのデータフレームに統合する

import numpy as np
import pandas as pd
import math

df = pd.read_csv('two-sample_problem_and_rank-sum_test.csv')
display(df)
arr1 = df['第1標本']
arr2 = df['第2標本']

# 第1標本と第2標本を元がどちらの標本であるかの情報を保持したまま、1つのデータフレームとして結合する
df1 = pd.DataFrame()
df1['sample'] = arr1
df1['flag'] = 1

df2 = pd.DataFrame()
df2['sample'] = arr2
df2['flag'] = 2
df2 = df2.dropna(how = 'any')

df = pd.concat([df1, df2], axis = 0)

元々のデータフレームが第1標本と第2標本を別々の列で保持していたため、1つの列に結合します。

この際に、flag列に元々の標本IDを入れることによって、後で第1標本の順位を計算できるようにしています。

統合したデータフレームを値の小さい順に並び替える

# 小さい順に並び替える
df = df.sort_values('sample')
df = df.reset_index(drop = True)
display(df)

全体を小さい順に並び替えます。

第1標本の順位の算出に必要な作業です。

第1標本の順位を配列に格納する

# 第1標本の順位を配列に格納する
r_arr = []
for index, row in df.iterrows():
    num = index + 1
    flag = row.flag
    if flag == 1:
        r_arr.append(num)

flag列を参照しながら、第1標本の順位を配列r_arrに格納します。

配列のインデックス番号$+1$が順位であることに気をつけましょう。

$m, n, M, W, E(W), V(W), 標準偏差sd$の値を求める

# m, n, M, Wを求める
m = len(df1)
n = len(df2)
M = m + n
W = np.sum(r_arr)
print(f'W = {W}')
print(f'm = {m}')
print(f'n = {n}')
print(f'M = {M}')


# Wの期待値E(W)と分散V(W)と標準偏差sdを求める
EW = m * (M  +1) /2
VW = m * n * (M + 1) / 12
sd = math.sqrt(VW)
print(f'E(W) = {EW}')
print(f'V(W) = {VW}')
print(f'sd = {sd}')

$m, n, M, W$の値を求めた上で、それらの値を使って期待値$E(W)$と分散$V(W)$、標準偏差$sd$を計算します。

検定を行う

# 検定を行う
abs_w_ew = abs(W - EW)
print(f'|W- E(W)| = {abs_w_ew}')

z = 1.96 * sd
print(f'z = {z}')

if abs_w_ew >= z:
    print(f'有意水準5%で母集団が等しいという仮説は棄却される')
else:
    print(f'有意水準5%で母集団が等しいという仮説は棄却されない')