
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、ベイズ統計学の入門的な内容をPythonで実装しながら学べる『Pythonによるベイズ統計学入門』を読んで、現役データサイティストが得た学びについてご紹介していこうと思います!
本書は頻度統計学にはないベイズ統計学特有の概念について、Pythonでコードを実装して可視化を行いながら理解を進めることができるので、数式・コードの両面からベイズ統計学に関する理解を進めることができる1冊になっています。
本記事ではその中から特に学びになった内容を噛み砕いて解説していきますので、ぜひ気軽にご覧になってください!
本書の概要
本書の目的は、データサイエンティストに不可欠の分析手法としてのベイズ的アプローチによるデータ分析の理論体系、すなわちベイズ統計学を正しく理解するとともに、Pythonというツールを活用してデータという宝石から王冠を作れる人材となるための基礎固めをすることである。
中妻照雄『Pythonによるベイズ統計学入門』(朝倉書店/2024) P3
本書はベイズ統計学を学ぼうとするデータサイエンティスト向けの本であり、その内容の理解には頻度統計学に関する基本的な理解を必要とします。
一方で、内容を理解しないままベイズを適用するのは危険を孕みますが、ベイズ統計学の概要をPythonコードや実行結果を通じて理解する、という文脈でも本書を活用することは可能かと思われます。
本書で扱っている内容の外観を掴んでいただくために、本書の章立てを見てみましょう。
- 「データの時代」におけるベイズ統計学
- ベイズ統計学の基本原理
- 未知の比率に対する推論
- ベイズの定理による事後分布の導出
- 未知のパラメータに関する推論
- 将来の確率変数の値の予測
- 付録(損失関数に対応した点推定の導出/SDDRの導出)
- 様々な確率分布を想定したベイズ分析
- ポアソン分布のベイズ分析
- 正規分布のベイズ分析
- 回帰モデルのベイズ分析
- 付録(ポアソン分布に従う確率変数の予測分布の導出/正規分布に従う確率変数の予測分布の導出/回帰係数と誤差項の分散の事後分布の導出/回帰モデルの予測分布の導出)
- PyMCによるベイズ分析
- ベイズ統計学とモンテカルロ法
- PyMCによる回帰モデルのベイズ分析
- 一般化線形モデルのベイズ分析
- 時系列データのベイズ分析
- 時系列データと状態空間表現
- 状態空間モデルに関する推論
- PyMCによる状態空間モデルのベイズ分析
- 付録(カルマン・フィルターの導出/予測分布の導出/カルマン・スムーザーの導出)
- マルコフ連鎖モンテカルロ法
- マルコフ連鎖と不変分布
- メトロポリス–ヘイスティングズ・アルゴリズム
- ギブズ・サンプラー
上記のように、ベイズの定理という基礎の基礎から、MCMC(マルコフ連鎖モンテカルロ法)などのベイズ統計学の文脈で最近よく使われる手法まで、ベイズ統計学の基礎にあたる部分を網羅的に扱っています。
また、本書のPythonコードに対してはかなり丁寧なコードの解説を入れているため、Pythonを扱うのが初めての人でもPythonコードの内容について理解できるようになっています。
本書から得た学び
私が本書から得た学びは以下の3つです。
- pyMCを活用したベイズ分析の流れ
- Gelman-Rubinの収束判定の基準$\hat{R}$という概念
- 不変分布という概念
順を追って解説していきます。
pyMCを活用したベイズ分析の流れ
本書の後半では、Pythonでベイズ分析を行うときに非常にありがたすぎるライブラリ、pyMCを使用してベイズ分析を行なっていきます。
Rでベイズ分析をするときは設定するためのコードが多くて結構大変だと認識している(Stanを使用しない場合)のですが、pyMCであれば本書で著者が触れているように『拍子抜けするほど』簡単にベイズ分析を行うことができます。
また、本書ではpyMCを使用した事前分布やMCMC(マルコフ連鎖モンテカルロ法)に基づいた乱数系列の作成と事後分布の出力を繰り返し行うため、pyMCの記法に自然と慣れていくことができます。
これから業務でベイズ分析を行いたい方にとっては、pyMCに触れる機会が提供されていることは非常に有益だと認識しています。
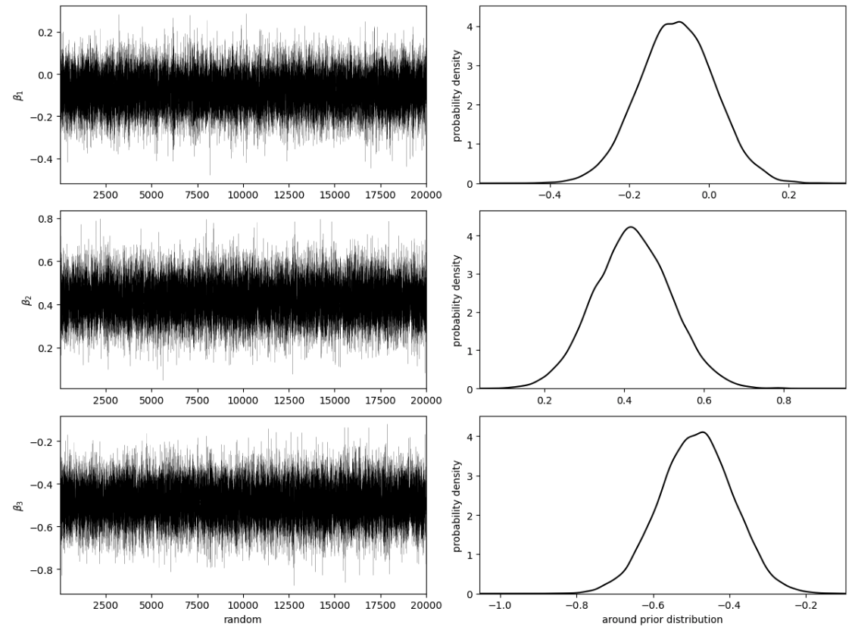
Gelman-Rubinの収束判定の基準$\hat{R}$という概念
重回帰分析でモデルを構築する場合には、精度の良いモデルになっているかどうかは調整済み$R^2$やRMSEなどでチェックを行うかと思います。
また、一般化線型モデルでモデルを構築する際には擬似$R^2$やAICで精度を確認したりと、頻度統計学や機械学習の範囲でモデルを作成する際には何らかの方法でモデルの精度について検証を行うかと思われます。
それでは、ベイズ分析においてはどのような指標で推定された統計量が妥当な値であるかを確認するのでしょうか?
そこで、本書で登場するのがGelman-Rubinの収束判定の基準$\hat{R}$です。
$\hat{R}$は以下のような式で計算されます。
$$\hat{R} = \sqrt{\frac{\hat{V}}{\hat{W}}}$$
ここで、$\hat{V}$と$\hat{W}$について説明する前に、事後統計量を推定するためにどのようにして乱数を生成しているのかについて確認をしていきましょう。
例えば、事後統計量を求めるために20000個の乱数系列を出力したいとします。
ですが、20000個の乱数を1から順番に出力するよりも効率的に乱数を出力したいと考えています。
そこで5000個の乱数系列を4つ同時並行で出力することによって、20000個の乱数系列を4分の1の時間が作成することを考えます。
この時の、1~5000の乱数系列、5001~10000の乱数系列、10001~15000の乱数系列、15001~20000の乱数系列をそれぞれ(そのままですが)系列と呼びます。
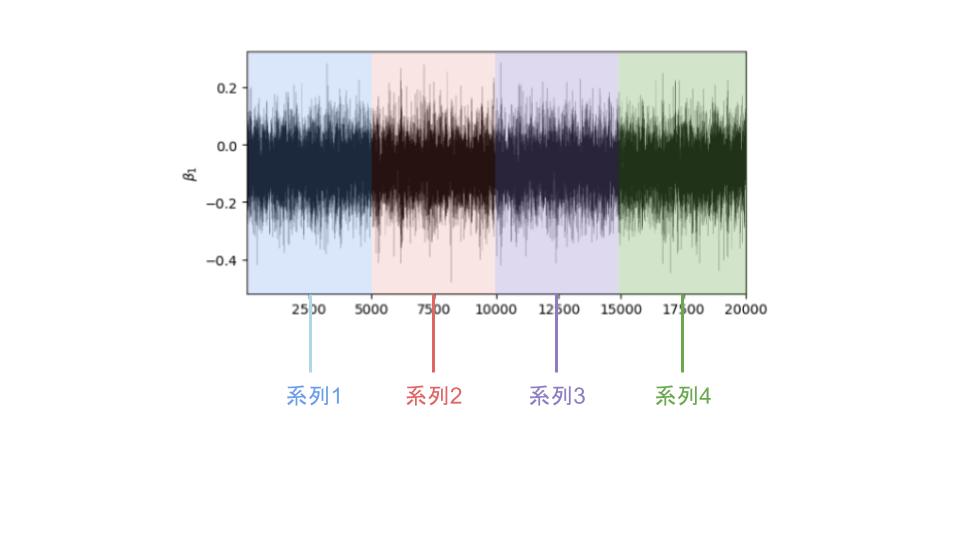
ここで、1~5000の系列に着目すると、乱数が生成されているので当然のことながら値にはばらつきが存在します。
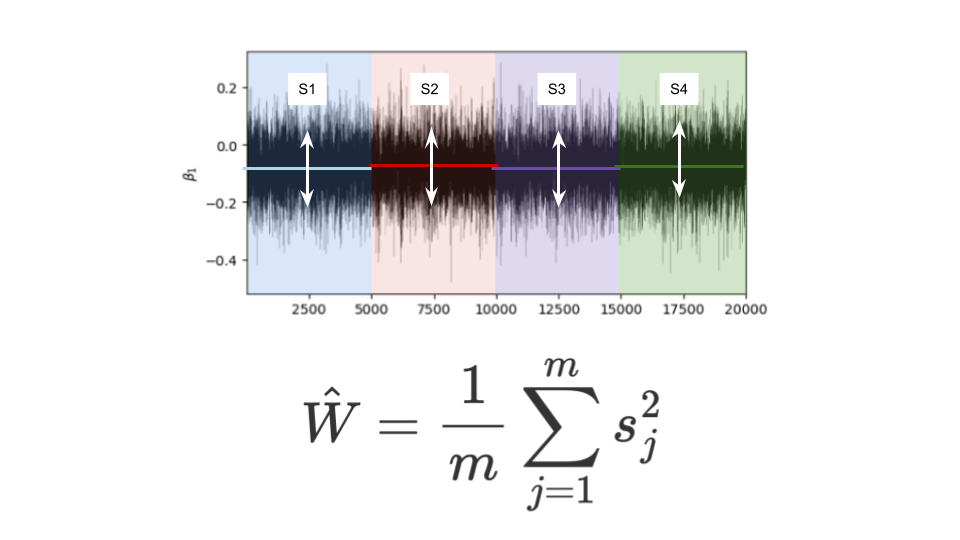
この時、それぞれの系列内におけるばらつきの平均のことを級内分散$\hat{W}$と呼びます。
$$\hat{W} = \frac1{m}\sum_{j = 1}^m s_j^2$$
$$※mは系列の数、今回であればm = 4$$
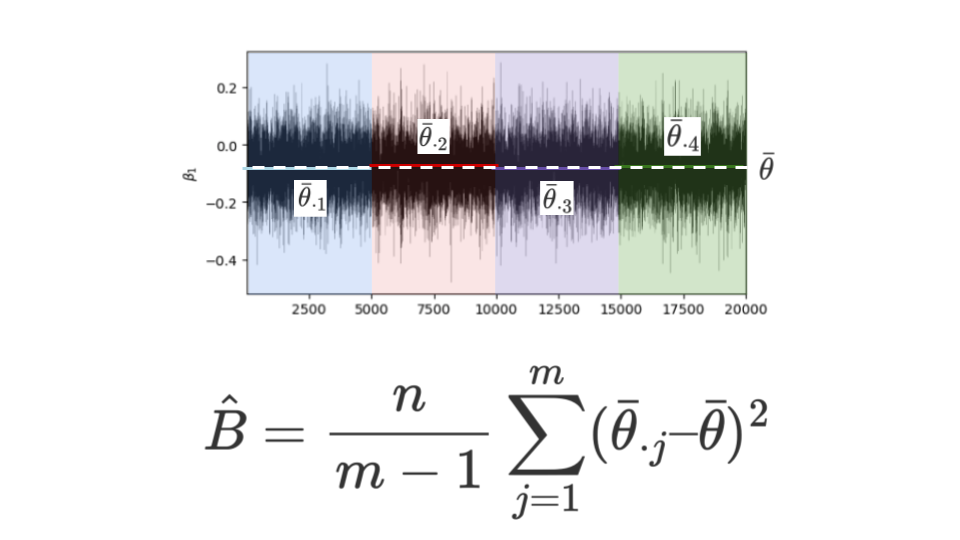
一方で、4つの系列がそれぞれ完全に同一でない以上、系列内だけでなく系列間にも多少のばらつきは発生します。
そのような系列間の平均のばらつきのことを級間分散$\hat{B}$と呼びます。
$$\hat{B} = \frac{n}{m-1}\sum_{j=1}^m (\bar{\theta}_{\cdot j} – \bar{\theta})^2$$
$$※nは系列内での乱数生成数、今回のケースであればn = 5000$$
そして、級内分散$\hat{W}$も級間分散$\hat{B}$も両方考慮した指標が以下の$\hat{V}$で表される値です。
$$\hat{V} = \frac{n}{n-1}\hat{W} + \frac1n \hat{B}$$
そして、$\hat{V}$を$\hat{W}$で割り算し、分散に存在する2乗を1乗に戻すためにルートをとった
$$\hat{R} = \sqrt{\frac{\hat{V}}{\hat{W}}}$$
の式が収束の条件として導かれるのです。
さて、事後分布からの乱数生成が適切に行われているときには$\hat{R}$の値は1に近い値をとる必要があるのですが、それはなぜでしょうか?
乱数を生成している以上、級内分散$\hat{W}$があるのは仕方がないことですが、級間分散$\hat{B}$については並列で作成した乱数系列の平均の間にばらつきがあることになってしまうのであまり望ましくありません。
つまり、理想的な状態では$\hat{B}$の値は0に近い値になっている必要があるのです。
$\hat{B}$の値が0に近い値になっているとき、系列内の乱数の個数$n$を無限大に飛ばすと、$\hat{V}$の値は$\hat{W}$に限りなく近づきます。
すると、
$$\hat{R} = \sqrt{\frac{\hat{W}}{\hat{W}}} = 1$$
となるため、系列間の平均にばらつきがない(=並列で乱数を生成したとしても、どの系列を同じように乱数を生成できている)ときには$\hat{R}$は1となり、事後統計量が正しく推定できたことになるのです。
不変分布という概念
マルコフ連鎖モンテカルロ法(MCMC)においては最初は適当な初期値と事前分布からスタートして、だんだんとパラメータの値を修正していくことによって、最終的には安定した事後分布から乱数系列を生成できるようになります。
このとき、そのような安定した事後分布のことを不変分布または定常分布と呼びます。
例えば、先ほど登場した乱数系列は不変分布であるということができます。
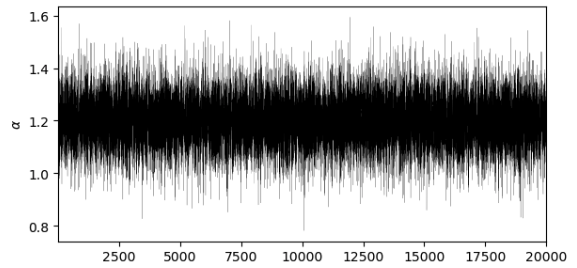
一方で、以下の乱数系列のように、1~2000の間の乱数系列の平均と2000以降の乱数系列の平均が大きく異なったり、その後の乱数系列の平均は0.5程度であるにも関わらず、時折1.4付近に値が飛んでしまうような場合は定常分布とは言えません。
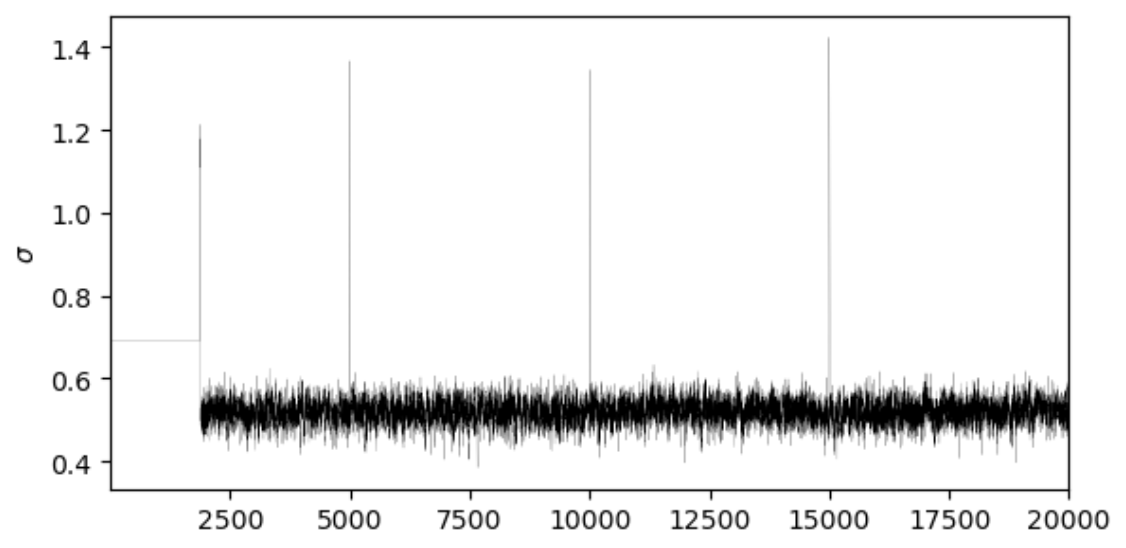
上記のような乱数系列を定常分布にするためには、乱数の値が安定するまでの乱数系列を切り捨てて、安定後の分布に基づいて乱数を生成する必要があります。
そのような乱数がある分布に収束したと判断されるまで乱数を生成し続ける期間のことを検査稼働期間(バーンイン)と呼びます。
例えば、先ほどの乱数系列に対してバーンインを1000に設定した場合の乱数系列は以下の通りになります。
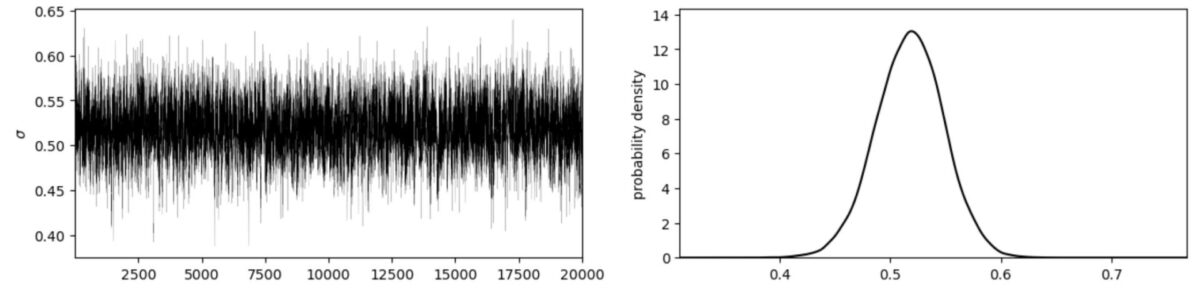
左図を見ると、乱数が0.4~0.6の幅に落ち着いていることが確認できるかと思われます。
このように、MCMCにおいては乱数系列が安定するまでのバーンインが必要であることは覚えておきましょう。
まとめ
今回の記事では、ベイズ統計学の入門的な内容をPythonで実装しながら学べる『Pythonによるベイズ統計学入門』を読んで、現役データサイティストが得た学びについてご紹介していきました!
本書はPython初心者でもpyMCで簡単にベイズ分析について学べる良書となっておりますので、気になった方はぜひお手に取っていただけると幸いです!



コメント