「自然科学の統計学」第8章演習問題4の個別ケース予測をPythonで実装してみた

元教師

こんにちは！データサイエンティストの青木和也（https://twitter.com/kaizen_oni）です！

今回の記事では、統計学の青本「自然科学の統計学」の第8章-演習問題4「個別ケース予測」をPythonで実装して解いてみたので、その手順について解説いたします！

今回の問題はプロビットモデルとロジットモデルを使って実際に予測を行う問題になっているので、第8章の他の問題よりもより実践的で、読者の皆さんにとっても活用の場面があるものかと思われます。

ぜひ、本演習を通してプロビットモデルとロジットモデルの予測方法について熟達していただければ幸いです！

問題文
実装コード
解説
まとめ

問題文

＜個別ケース予測＞

プロビット・モデルとロジットモデルによって以下表のコース選択データを分析した結果を用いて、データの30人の学生のコース選択を予測せよ。

実際のコース選択との一致は、30人中何例、何%となるか
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章演習問題 P249~250

プロビットモデル・ロジットモデルとは？

プロビットモデルとは、1/0のような二値$Y_i$を予測するような回帰問題において、説明変数が$X_i$であるとすると、条件付き確率

$$P(Y_i|X_i) = F^*(X_i)$$

の$F^*(X_i)$に標準正規分布を仮定する時の予測モデルのことを言います。

$$標準正規分布の累積分布関数~~~F^*(X_i) = \Phi(\beta_0 + \beta_1 X_i) = \int_{-\infty}^{\beta_0 + \beta_1 X_i} \frac1{\sqrt{2\pi}}e^{-x^2/2}dx$$

一方で、$F^*(X_i)$にロジスティック分布を仮定するとき、そのモデルをロジットモデルと呼びます。

$$ロジスティック分布の累積分布関数~~~F^*(X_i) = \Lambda(\beta_0 + \beta_1 X_i) = \frac{e^{\beta_0 + \beta_1 X_i}}{1 + e^{\beta_0 + \beta_1 X_i}}$$

この2つの関数が条件付き確率の分布の仮定に使用されている大きな理由は、累積分布関数が0~1に収まるという性質が、「確率は0%~100%に収まっていて欲しいよね」という点とマッチするからです。

今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。

実装コード

今回の問題を解くためのコードは以下の通りです

import pandas as pd
from statsmodels.formula.api import ols, logit, probit

def summarize(formula, df, target):
    
    # 説明変数と目的変数に分割
    X = df.drop(target, axis = 1)
    y = df[target].to_numpy()
    n = len(y)
    
    # プロビットモデルの作成
    res_probit = probit(formula, data = df).fit()
    print(res_probit.summary())
    
    # 予測値の算出
    ppred = res_probit.predict(X)
    #　閾値の設定
    threshold = 0.5
    # 閾値によって生徒のコース選択を決定
    ppred = [ 1 if p > threshold else 0 for p in ppred]
    
    # 正答数を計算
    pcount = 0
    for r, p in zip(y, ppred):
        if r == p:
            pcount += 1
    print(f'閾値{threshold * 100}%における正答数: {pcount}')
    print(f'閾値{threshold * 100}%における正答率: {pcount * 100/ n}%')

    # ロジットモデルの作成
    res_logit = logit(formula, data = df).fit()
    print(res_logit.summary())
    
    # 予測値の算出
    lpred = res_logit.predict(X)
    lpred = [ 1 if p > 0.5 else 0 for p in lpred]
    
    # 正答数を計算
    lcount = 0
    for r, p in zip(y, lpred):
        if r == p:
            lcount += 1
    print(f'閾値{threshold * 100}%における正答数: {lcount}')
    print(f'閾値{threshold * 100}%における正答率: {lcount * 100/ n}%')
    
df = pd.read_csv('Students_choice_of_two_courses_A_and_B.csv', index_col = 0)
formula = 'コース選択 ~ 性別 + 前期試験成績 + 専攻'

summarize(formula, df, 'コース選択')

解説

今回の問題は以下3ステップで解いています

データから各モデルを作成
コース選択の確率を予測、50%を閾値としてコース選択を1/0の二値に変換
正答数・正答率を計算

順を追って解説していきます

データから各モデルを作成

import pandas as pd
from statsmodels.formula.api import ols, logit, probit

def summarize(formula, df, target):
    
    # 説明変数と目的変数に分割
    X = df.drop(target, axis = 1)
    y = df[target].to_numpy()
    n = len(y)
    
    # プロビットモデルの作成
    res_probit = probit(formula, data = df).fit()
    print(res_probit.summary())

    ...

    # ロジットモデルの作成
    res_logit = logit(formula, data = df).fit()
    print(res_logit.summary())

データからプロビットモデルとロジットモデルを作成します。

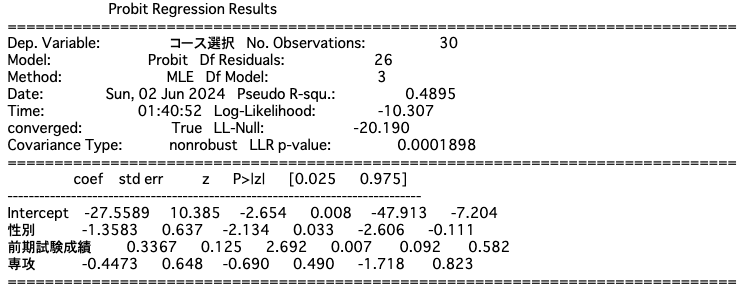
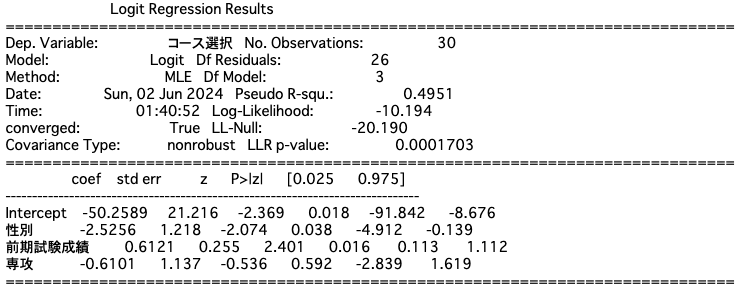
なお、関数の序盤でXとyに分割しているのは、この後で実測値yよ予測値predict(X)を比較するためです。

コース選択の確率を予測、50%を閾値としてコース選択を1/0の二値に変換

    # 予測値の算出
    ppred = res_probit.predict(X)
    #　閾値の設定
    threshold = 0.5
    # 閾値によって生徒のコース選択を決定
    ppred = [ 1 if p > threshold else 0 for p in ppred]

    ...

    # 予測値の算出
    lpred = res_logit.predict(X)
    lpred = [ 1 if p > 0.5 else 0 for p in lpred]

先ほど作成したモデルのpredictメソッドを使って、コース選択確率を予測します。

一方で、今回の問題においては「コースAを選択したか（=1）、していないか（=0）」というデータyと比較する必要があるため、「コース選択確率が50%より大きい場合はコースを選択したと予測する」という条件をおいて、選択確率を1/0の二値に変換していきます。

正答数・正答率を計算

    # 正答数を計算
    pcount = 0
    for r, p in zip(y, ppred):
        if r == p:
            pcount += 1
    print(f'閾値{threshold * 100}%における正答数: {pcount}')
    print(f'閾値{threshold * 100}%における正答率: {pcount * 100/ n}%')

   ...

    # 正答数を計算
    lcount = 0
    for r, p in zip(y, lpred):
        if r == p:
            lcount += 1
    print(f'閾値{threshold * 100}%における正答数: {lcount}')
    print(f'閾値{threshold * 100}%における正答率: {lcount * 100/ n}%')
    
df = pd.read_csv('Students_choice_of_two_courses_A_and_B.csv', index_col = 0)
formula = 'コース選択 ~ 性別 + 前期試験成績 + 専攻'

summarize(formula, df, 'コース選択')

先ほど作成した二値の予測値と実測値yを比較し、一致したデータ数をカウントしていきます。

再度に、一致したデータ数を総データ数で割り算して、一致率を計算します。

||| プロビットモデルの一致数・一致率