
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学界の青本「自然科学の統計学」を読んで現役DSが得た学びをご紹介していきたいと思います。
本書は東大出版の統計学シリーズの2作目にあたる本で、統計学界の赤本「統計学入門」で統計学の基礎について学んだのちに待ち受ける、統計学の発展的な内容について解説された1冊になります。
本書は初版1992年に発行された歴史ある統計学書でありながら、統計学者必見の書として語り継がれており、丁寧な説明、図表、ふんだんな演習問題によって統計学に対する理解を統計学入門以上に深めることができる1冊となっています。
本記事では本書から私が得た学びのエッセンスをみなさんにご紹介させていただきたいと思います!
本書の概要
本書は東大出版の統計学シリーズ「統計学入門」「自然科学の統計学」「人文・社会科学の統計学」の中の中間に位置する1冊となっています。
統計学入門が頻度統計学の基礎を外観できる一冊であるのに対して、自然科学の統計学は統計学入門の復習的内容なありつつも、以下の章立てを見ていただけばわかるようにさらに踏み込んだ内容を取り扱っています。
- 確率の基礎
- 線形モデルと最小二乗法
- 実験データの分析
- 最尤法
- 適合度検定
- 検定と標本の大きさ
- 分布の仮定
- 質的データの統計的分析
- ベイズ決定
- 確率過程の基礎
- 乱数の性質
また本書にある演習問題は各章ごとに平均6問程度用意されており、以下のような種類の問題が含まれています。
- ゴリゴリと計算する問題
- ゴリゴリと証明を行う問題
- データを用いてプログラムなどで解決する問題
どの問題もある程度歯応えがあるため、かなりの時間楽しめる1冊となっています。
現役DSが本書から得た学び
本書は骨太でさまざまな学びを得られたのですが、特に私が学びを得たポイントは以下の3点です。
- 適合度検定によるモデルの妥当性の検証
- 1次元的な強さを算出できるブラッドリー・テリーモデル
- 質的データに対する予測モデル
順を追ってご紹介いたします。
適合度検定によるモデルの妥当性の検証
多項分布の各項の生起確率$p_1, p_2, \cdots, p_a$がある一定の法則に従っているという仮説の検定は一般に適合度検定 test of goodness of fit とよばれており、いろいろな応用がある
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 P145
上の引用文でいう「生起確率」とは、例えば「10回コインを投げる試行を100回行った時に1~10回コインが出るそれぞれの確率」のような実測値のことを指します。
上記の例で言えば、10回コインを投げる時のそれぞれの確率は確率$\frac12$の二項分布に従っていると考えられるので、生起確率に基づいて「確率$\frac12$の二項分布という仮定が正しいのか」を検証することを適合度検定といいます。
適合度検定は次の2ステップで考えることができます。
- 仮定に基づいて理想的な度数(理論度数)を算出する
- 理論度数と実測値から適合度$\chi^2$を算出し、$\chi^2$分布と比較することによって仮定を棄却するか否かを決定する
順を追って解説していきます。
仮定に基づいて理想的な度数(理論度数)を算出する
「生起確率に関する仮定」についてはさまざまな仮定をおくことができ、本書においても以下のように多様な仮定が置かれています。
- 円周率$\pi$には0~9の数字が一様に登場するという仮定
- 原子核破壊で毎7.5秒ごとにある地点に到達する粒子の個数はポアソン分布に従うという仮定
- 解析学と代数学のテストの成績配分には関連がないという仮定
- ドラム缶製造工程を改良したことによる効果はないという仮定
- 腸チフスの予防接種には効果がないという仮定
- 職業によって癌の重症度に違いはないという仮定
- 野球チームの強さは一次元的なパラメータで表現できるという仮定
これらの仮定に基づいて、「その仮定が真であったならば、理想的にはどのような値になっているべきか」という値を計算します。
この値のことを理論度数といい、適合度検定に使用します。
理論度数と実測値から適合度$\chi^2$を算出し、$\chi^2$分布と比較することによって仮定を棄却するか否かを決定する
適合度$\chi^2$は以下の式によって計算することができます。
$$ \chi^2 = \sum_i^{n} \frac{(実測値_i – 理論度数_i)^2}{理論度数_i}$$
式を見てわかるように、実測値と理論度数の差が大きいほど適合度$\chi^2$の値は大きくなるようになっています。
そして、$\chi^2$分布の値を調べるにあたっては自由度$\nu$というパラメータを検証したい仮定から求めます。
$$\nu = (多項分布の自由度) – (あてはめたモデルのパラメータの個数)$$
ここでいう「多項分布の自由度」とは、先ほどの例で言えば「コインの表が出るありうる回数」($=$10回)のことですし、「あてはめたモデルのパラメータの個数」は「二項分布の確率$p=\frac12$」($=1$個)になります。
この自由度に基づいて、自由度$\nu$の$\chi^2$分布$\chi^2(\nu)$の上側$25%$点の値$\chi^2_{0.25}(\nu)$と先ほど求めた適合度$\chi^2$を比べることによって、仮定を棄却するか否かを決定するのです。

1次元的な強さを算出できるブラッドリー・テリーモデル
先ほどの適合度検定の仮定で、
野球チームの強さは一次元的なパラメータで表現できるという仮定
というものがありました。
この仮定に基づいてチームの強さのような指標を算出するのが、ブラッドリー・テリーのモデルです。
詳細は以下記事に譲るのですが、ある2チーム$i, j$が対戦した時の勝敗の確率$p_ij, p_ji$を強さのパラメータ$\theta_i, \theta_j$を以下の式で表されると仮定し、各チームの強さのパラメータ$\theta$を反復的な方法によって推定するという手法です。
$$p_ij = \frac{\theta_i}{\theta_i + \theta_j}, p_ji = \frac{\theta_j}{\theta_i + \theta_j}$$
質的データに対する予測モデル
「統計学入門」やその他書籍で重回帰分析のような目的変数が実数であるようなデータについては繰り返し学んできました。
一方で、目的変数が質的変数であるようなデータの予測については、統計学という文脈ではあまり学んできませんでした。
本書では質的変数を予測するようなモデル、ロジット・モデルとプロビット・モデルについても学ぶことができるため、自分自身のできることが広がったと認識しています。
例えば、「ある被験者は肥満かどうか」というのを、体重・身長・1日あたりの摂取カロリーなどの説明変数から予測をしたいとします。
ここで、肥満である場合は1、肥満でない場合は0という値が肥満カラム(列)に振られているとします。
この時、重回帰分析を使って肥満列の値を推定することもできるのですが、重回帰分析は説明変数に係数をかけて線形に(足し算で)組み合わせた式が予測式になるので時には0より小さくなったり、1より大きくなったりしてしまいます。
今回のケースにおいては肥満か肥満でないかの1/0を予測したいので、0~1の範囲をオーバーする予測値は少し解釈に困ってしまいます。
そのような場合に活用できるのが、ロジットモデルとプロビットモデルです。
ロジットモデルはロジスティック分布の累積密度関数を、プロビットモデルは標準正規分布の累積密度関数を用いるため、必ず0~1の区間に収めることができます。
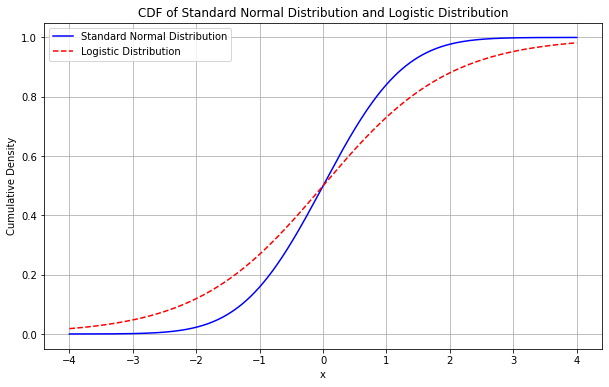
これらのモデルによって、「肥満である確率」を0~1の間の値で算出することができます。
そして、閾値(例えば0.5)を設け、その値を上回ったら肥満、下回ったら肥満でないのように判定することによって、肥満かどうかを1/0で予測することができるのです。
まとめ
今回の記事では、統計学界の青本「自然科学の統計学」を読んで現役DSが得た学びをご紹介していきました。
本書には他にも証明的な意味でも、計算的な意味でも、プログラムの実装的な意味でも実践的な演習や、気分転換にちょうどいいコラムなど、たくさんの魅力がある書籍になっています。
統計検定準1級のための予習としてちょうどいい書籍という噂も聞くので、統計学入門よりも一歩踏み込んだ統計の内容を学習したい方は、ぜひ本書を手に取ってみてください!




コメント