
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回は統計学の基本の「き」、平均値と並んで利用される値、中央値について解説していきたいと思います!
中央値は平均値の影に隠れていながらも、平均値ではカバーできない領域をカバーしている優秀な脇役なのです。
ぜひ中央値についてマスターして、データの分布によって代表値を使い分けられる人になっちゃってください!
中央値とは
中央値とは、データを代表する値(代表値)のうちの1つであり、読んで字の如く、データの真ん中の値を表します。
中央値はデータの数が偶数個か奇数個かによって若干定義が異なりますので、比較的分かりやすい奇数個の場合から定義を見ていきましょう!
中央値の定義(データの数が奇数個の場合)
データを値の大きい順または小さい順に順番に並べた時に、ちょうど真ん中にある数字を中央値とします。
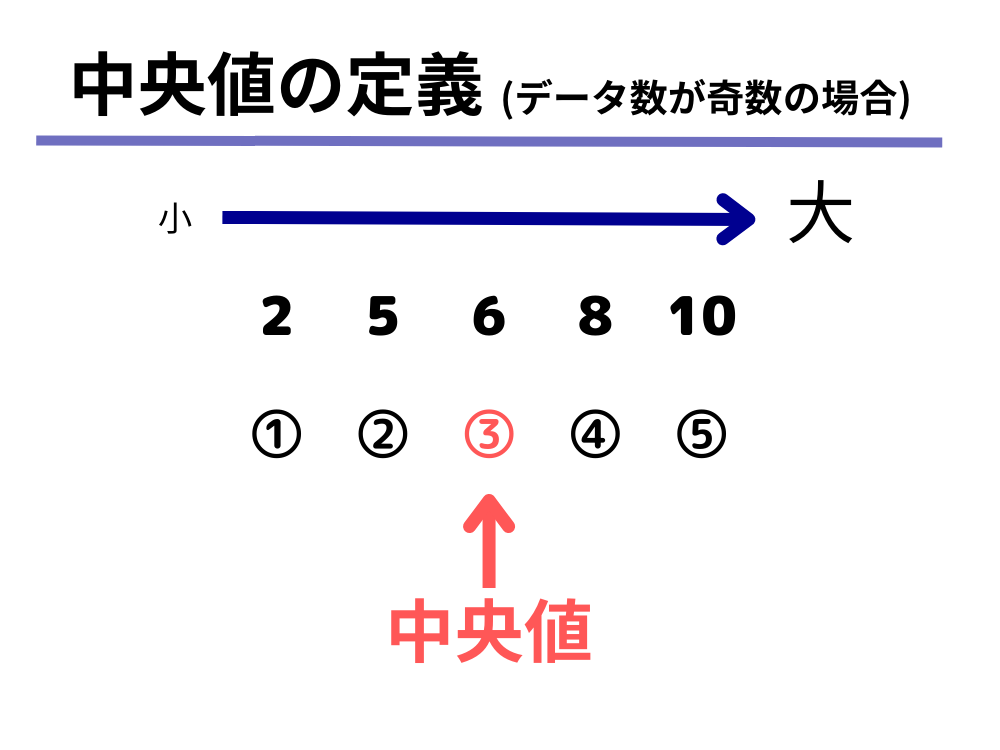
奇数の場合の定義は、まさしく「中央値」というにふさわしく、データのちょうどど真ん中の数字を持ってくればいいので非常に分かりやすいですね。
さて、次なる問題はデータの数が偶数個の場合の中央値の定義ですが、ここで立ち止まって、皆さんで偶数の場合の定義を考えてみてください。
偶数の場合は、どのようにして「中央値」たる指標を定義すれば良いでしょうか?
さて、いかがでしょうか。
データが偶数個の場合は、「まさにここでデータのど真ん中や!」と言える1つの数字を指定することができませんので、奇数個の場合とは異なった定義をしなければなりません。
それでは、偶数個の場合の定義を見ていきましょう。
中央値の定義(データの数が偶数の場合)
データを値の大きい順または小さい順に順番に並べた時に、データの真ん中に当たる2つの数字の平均値を中央値とします。
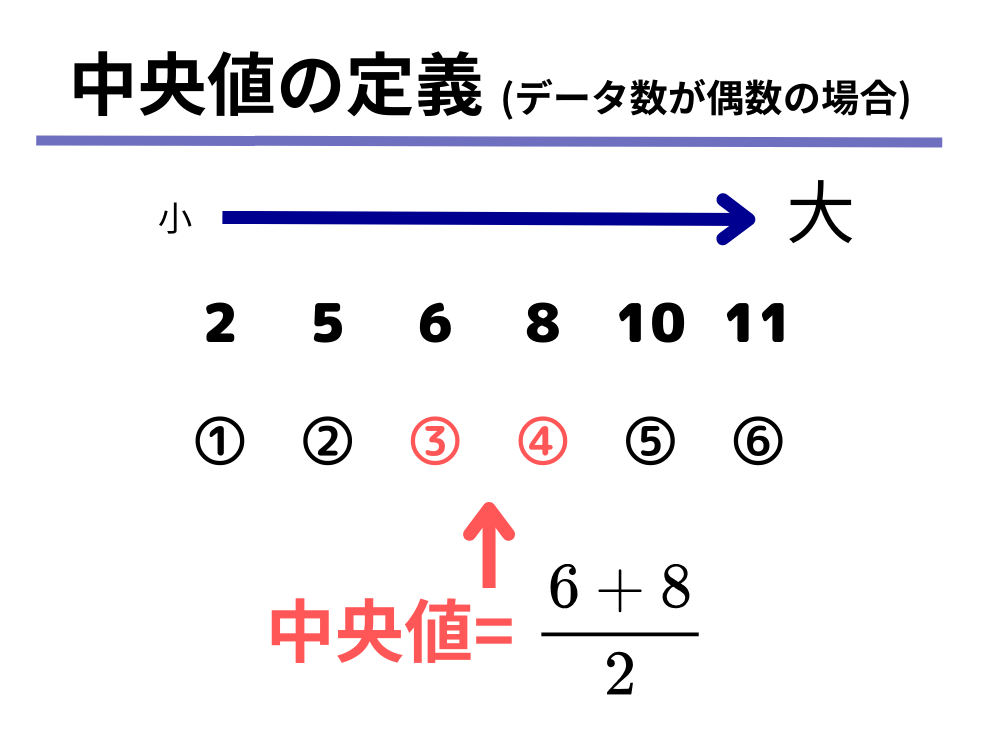
データの数が偶数個の場合は、「中央値らしき値」は2つ出てしまいますので、その2つの値の平均値を取る、というのは納得のいく定義かと思います。
平均値じゃダメなの?
同じようにデータの中心を表す代表値として平均値がありますが、平均値があれば中央値などなくてもデータの中心を表すことができるのではないでしょうか。
例えば、データをヒストグラムで表した時に、以下のような分布であれば平均値も中央値も一致するので、平均値だけでも事足りると思うかもしれません。
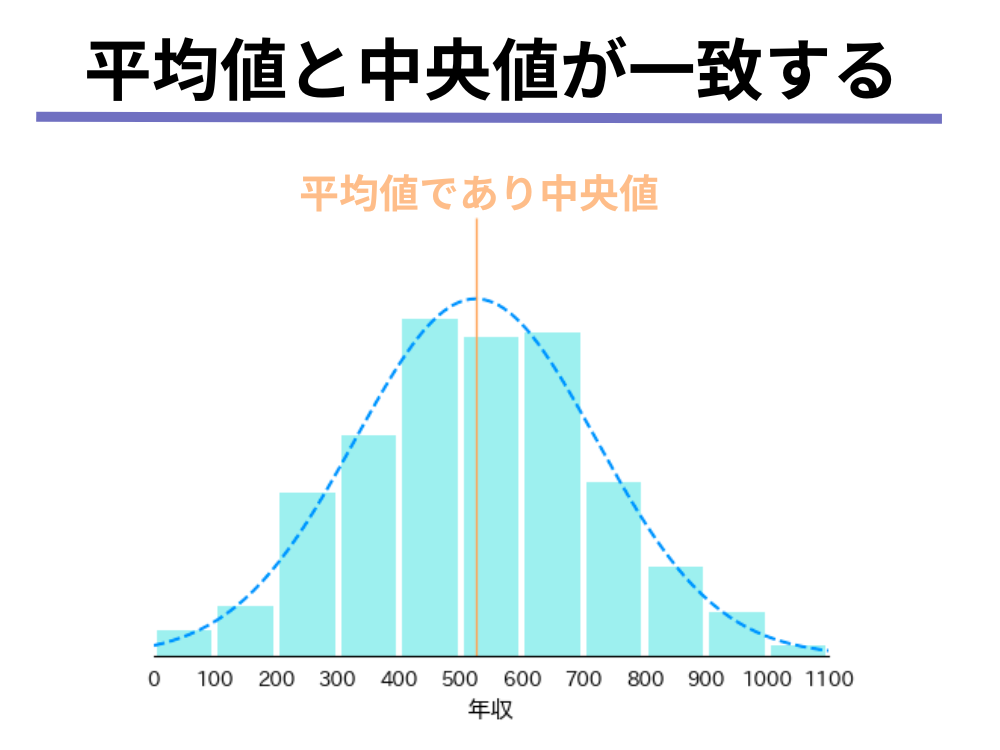
このような左右対称で分布の平均にピーク(山の頂上)があるような分布を、正規分布と言います。
しかし、「日本の所得分布」のように左右対称でなく偏りがある場合は、数は少ないが値が大きい方に平均値が引っ張られてしまうため、平均値と中央値が離れてしまうケースがあります。

上記の分布の場合には、全体から見ると少数派ですが一部の高所得者層(特に年収2000万円以上の人たち)に平均値が引っ張られて、中央値よりも120万円ほど高くなっていることがいることが分かります。
こうした時に、何を持って「データの中心」というべきかを考えると、その値より大きい年収と小さい年収の人の数が等しい中央値の方がデータの中心としては適していると言えるのではないでしょうか。
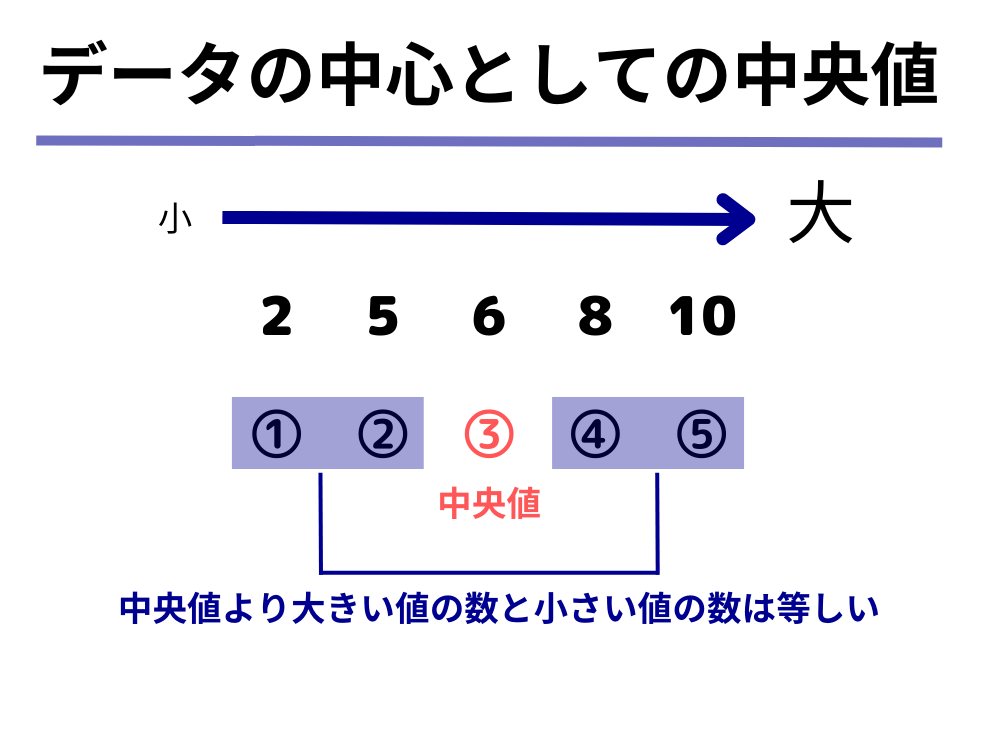
中央値に関する統計検定の類似問題
それでは実際の統計検定3級で出題された中央値の類似問題を解きながら、中央値についての理解を深めましょう!
次の幹葉図は、北海道網走市における2023年2月1日〜2月28日までの28日間の最深積雪(単位: cm)を表したものです。例えば、41(cm)という値は、十の位に4を書き、一の位に1を書く。

資料:気象庁「過去の気象データ検索」
[1] この28日間の網走市における最深積雪の最頻値はいくらか。
[2] この28日間の網走市における最深積雪の中央値はいくらか。
「最頻値」という聞きなれない言葉があるかもしれませんが、最頻値は「最もよく出現する値」という意味です。
それを踏まえて問題を解いてみましょう!
[1] 最頻値は「最もよく出現する値」なので、各積雪量の出現回数をカウントしてみると以下の表のようになります。
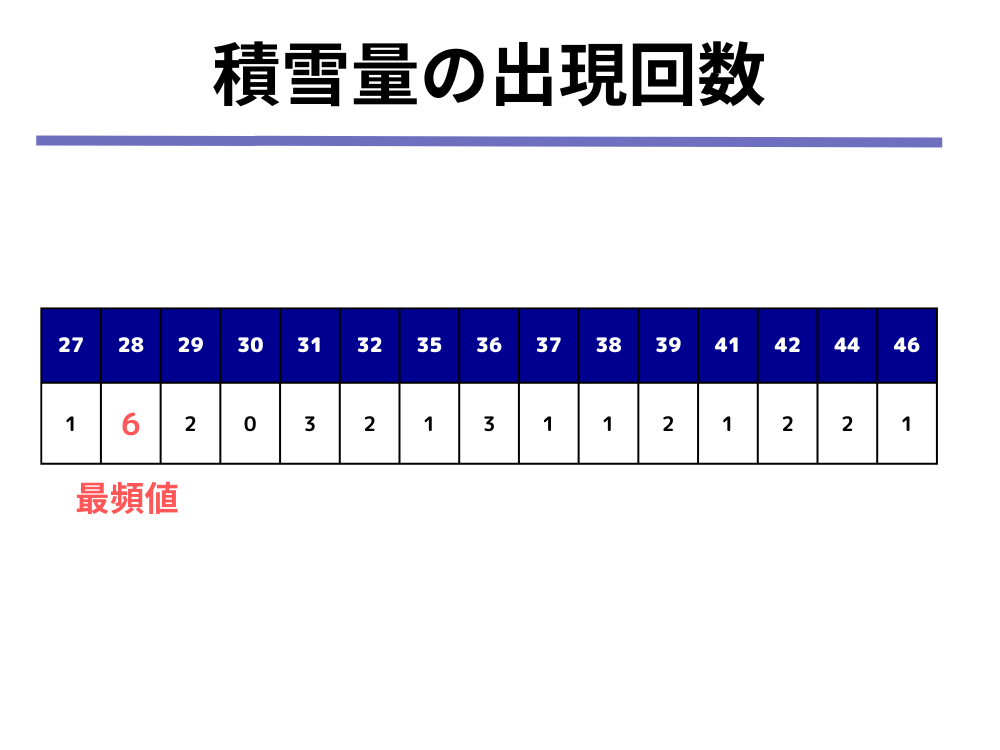
28(cm)が6回と最も多く出現しているので、最頻値は28となります
[2] データ数は「28日間」なので、データの真ん中の値は14番目の値と15番目の値の2つであることが分かります。
14番目の値は32、15番目の値は35なので、求める中央値は( 32 + 35 ) ÷ 2 = 33.5 となります
Python/R/SQLでの中央値の算出方法
先ほどは網走市の最深積雪量のデータに対して手計算で最頻値、中央値を求めましたが、今度はPython/R/SQLを使って、最頻値、中央値を求めてみましょう!
まずは、pandasでCSVを読み込んで、mode()とmedian()を使用して最頻値と中央値を求めましょう。
#csvを読み込むためにpandasライブラリをインポート
import pandas
#csv読み込み
df = pd.read_csv('snowfall.csv')
#mode()で最頻値を、median()で中央値を算出
print('最頻値: {}'.format(df['snow'].mode()[0]))
print('中央値: {}'.format(df['snow'].median()))最頻値: 28
中央値: 33.5df[‘カラム名’].mode() でdf[‘カラム名’]の配列(より正確にはpandas.Series)の最頻値を出力します。
今回の例で言えば、最深積雪量の最頻値を出力します。
mode()関数の後ろに[0]がついている理由は、最頻値が複数の値を取る可能性があるからです。
例えば、以下のような場合はmode()関数は最頻値を2つ返します。
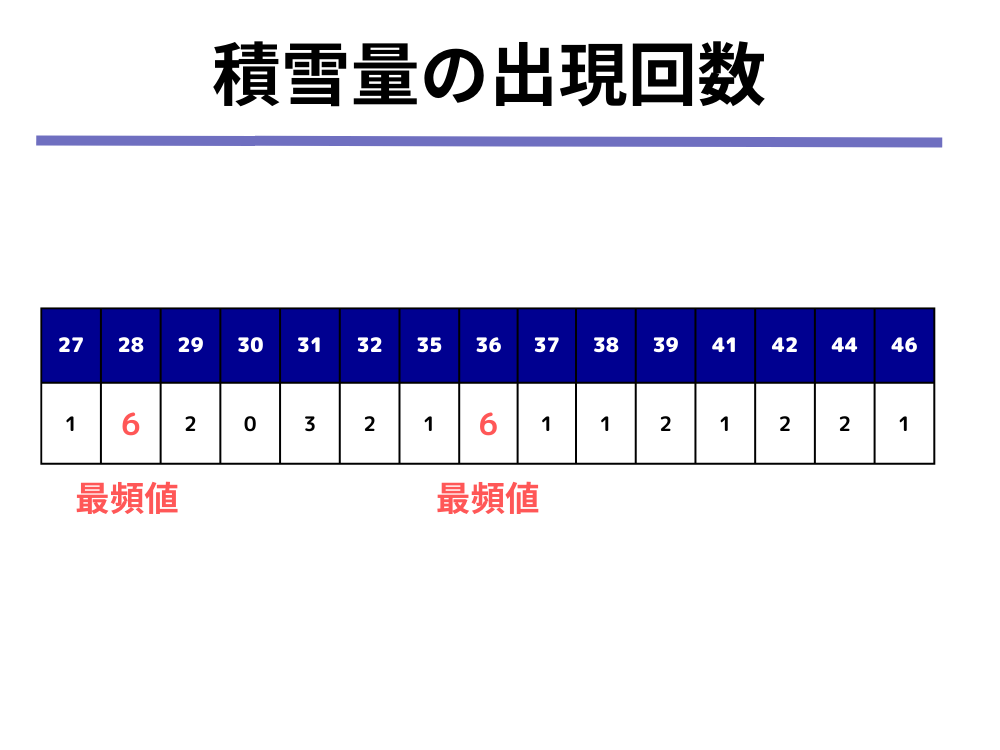
この時、mode()関数は「1つ目の最頻値は28、2つ目の最頻値は36」というように、最頻値に番号をつけて返してくれます。
ただし、Pythonの場合はそのような番号は0番目から始まるので、「0番目の最頻値は28、1番目の最頻値は36」という風にカウントしてくれます。
この仕様は最頻値が1つの場合でも同様で、今回の例では「0番目の最頻値は28」と返してくれているので、mode()[0]と指定することによって0番目の最頻値、すなわち28を取りに行っているのです。
read_csvでCSVファイルを読み込んだ後に、mode()やmedian()で最頻値と中央値を求めましょう。
#csvを読み込み
df <- read.csv('./snowfall.csv')
#最頻値を計算
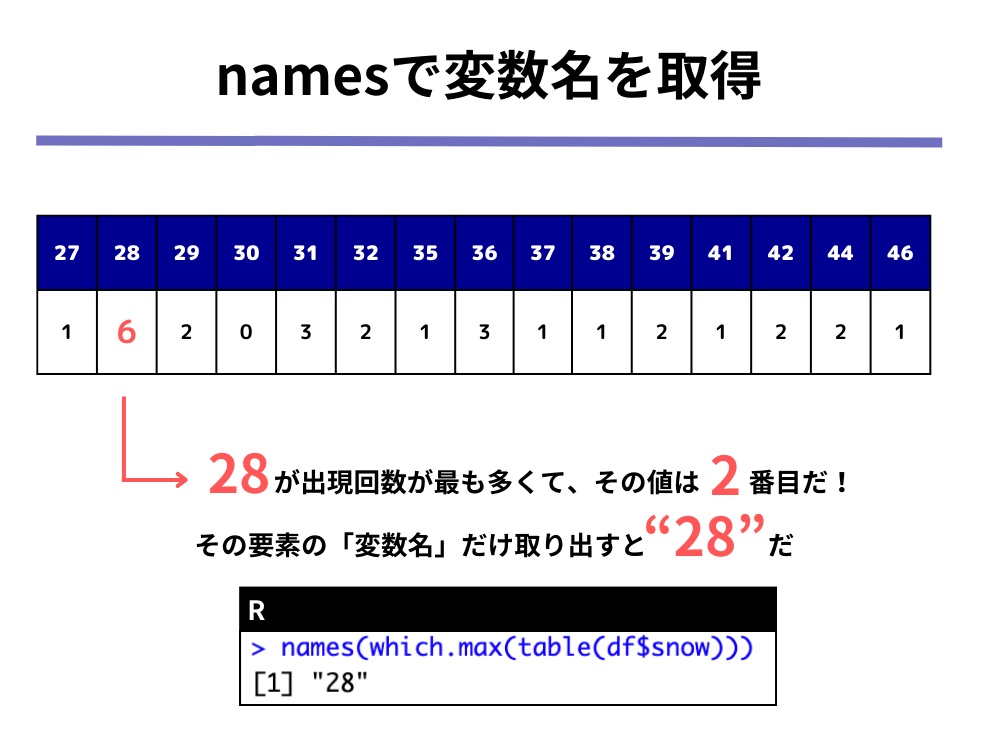
names(which.max(table(df$snow)))
#中央値を計算
median(df$snow)>names(which.max(table(df$snow)))
[1] "28"
>median(df$snow)
[1] 33.5中央値の算出方法については問題ないかと思いますが、最頻値の計算方法については、Rに最頻値を簡単に求める関数がないために少し複雑になっているので、段階を追って解説していきます。
- table(df$snow)
- which.max(table$snow)
- names(which.max(table$snow))
「1.table(df$snow)」では以下のような各最深積雪量とその出現回数についてカウントした表を作成しています。
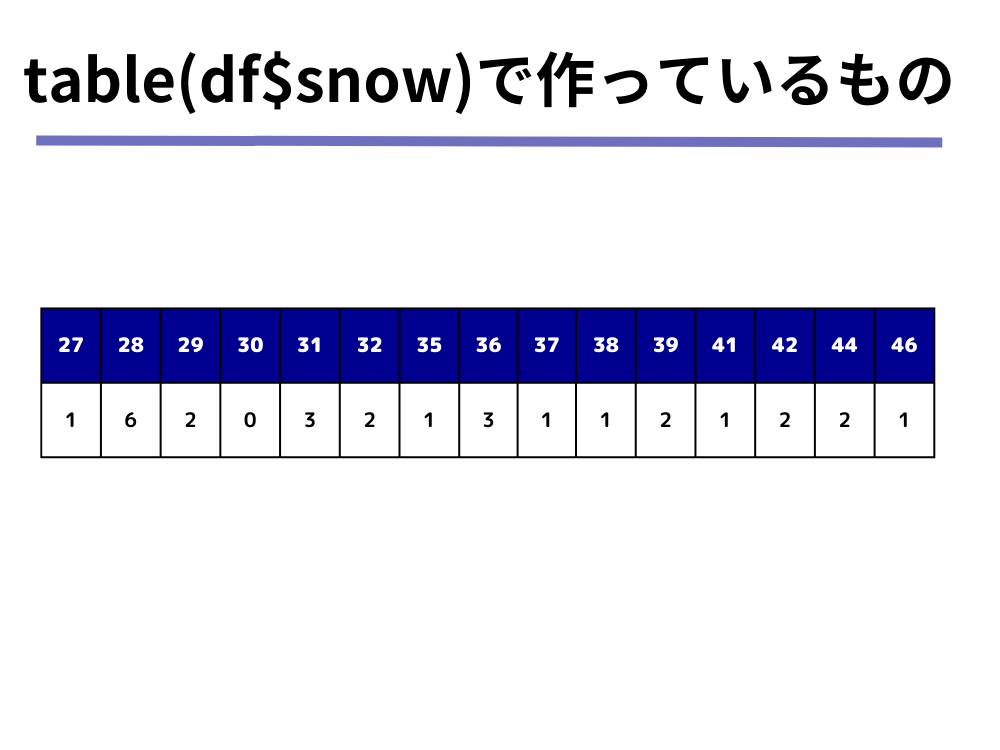
「2.which.max(table(df$snow))」では、①上の表の中で出現回数が最も多い値と、②その値が表の左から数えて何番目にあるのか、の2つの値を抽出しています。
なお、Rの場合はPythonと異なり、最初の要素を「1番目」としてカウントします。
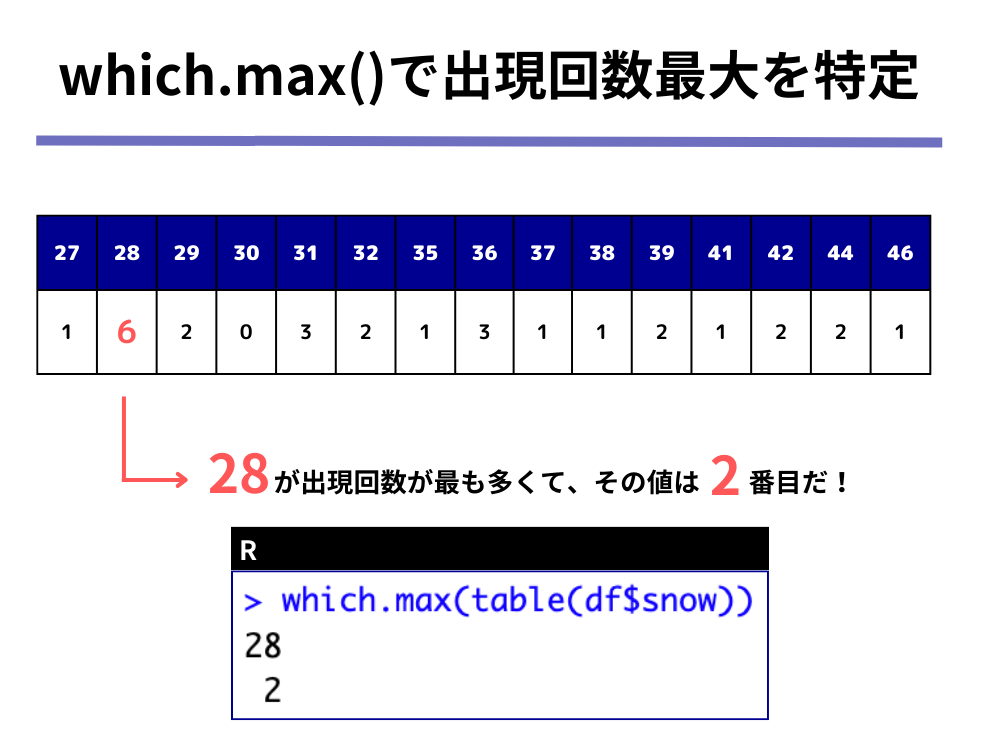
「3.names(which.max(table(df$snow)))」では、先ほど取り出した「28 2」という要素のうち、変数名(=names)にあたる「28」を取り出します。
次のSQL文を実行して、SNOWFALLテーブルを定義し、SNOW列の最頻値と中央値を計算してください。
CREATE TABLE SnowFall
(
date DATE,
snow INTEGER
);
INSERT INTO SnowFall VALUES('2023-02-01', 31);
INSERT INTO SnowFall VALUES('2023-02-02', 41);
INSERT INTO SnowFall VALUES('2023-02-03', 38);
INSERT INTO SnowFall VALUES('2023-02-04', 31);
INSERT INTO SnowFall VALUES('2023-02-05', 30);
INSERT INTO SnowFall VALUES('2023-02-06', 29);
INSERT INTO SnowFall VALUES('2023-02-07', 28);
INSERT INTO SnowFall VALUES('2023-02-08', 28);
INSERT INTO SnowFall VALUES('2023-02-09', 31);
INSERT INTO SnowFall VALUES('2023-02-10', 29);
INSERT INTO SnowFall VALUES('2023-02-11', 28);
INSERT INTO SnowFall VALUES('2023-02-12', 28);
INSERT INTO SnowFall VALUES('2023-02-13', 28);
INSERT INTO SnowFall VALUES('2023-02-14', 27);
INSERT INTO SnowFall VALUES('2023-02-15', 36);
INSERT INTO SnowFall VALUES('2023-02-16', 35);
INSERT INTO SnowFall VALUES('2023-02-17', 36);
INSERT INTO SnowFall VALUES('2023-02-18', 32);
INSERT INTO SnowFall VALUES('2023-02-19', 28);
INSERT INTO SnowFall VALUES('2023-02-20', 44);
INSERT INTO SnowFall VALUES('2023-02-21', 46);
INSERT INTO SnowFall VALUES('2023-02-22', 44);
INSERT INTO SnowFall VALUES('2023-02-23', 42);
INSERT INTO SnowFall VALUES('2023-02-24', 42);
INSERT INTO SnowFall VALUES('2023-02-25', 39);
INSERT INTO SnowFall VALUES('2023-02-26', 39);
INSERT INTO SnowFall VALUES('2023-02-27', 37);
INSERT INTO SnowFall VALUES('2023-02-28', 36);まずは最頻値から求めてみましょう。
SQLには最頻値を求める関数がないので、以下のようにクエリ文を組んで最頻値を取り出します。
SELECT
snow,
COUNT(*) AS cnt --①最深積雪量ごとの出現回数をカウント
FROM snowfall
GROUP BY snow
--すべての出現回数以上の出現回数、つまり最大の出現回数の行のみを表示
HAVING COUNT(*) >= ALL(SELECT COUNT(*) FROM snowfall
GROUP BY snow)
上記回答について、順を追って解説していきましょう。
まずは前半5行を見てみると、snowでGROUP BYして、snowの値ごとに出現回数をCOUNTしていることが分かります。

そして、後半の2行では、HAVING句の中で「snowの出現回数がすべての出現回数以上の行のみ取り出す」という指示をしています。
つまりは最も大きい出現回数6回の最深積雪量28cmのみが取り出されることとなります。
続いて、中央値を求めてみましょう。
SQLには(どのDBでも実装できる)中央値を求める関数ないので、次のようにクエリ文を組んで中央値を求めていきます。
--- ①
WITH OrderSnow AS (
SELECT
date,
snow,
--- ROW_NUMBER()関数によって、最深積雪量の小さい順に1から数字を割り当てる
ROW_NUMBER() OVER(order by snow) as order_id,
--- ct列に日数(=28)を入れる
(SELECT COUNT(*) FROM SnowFall) AS ct
FROM SnowFall
)
SELECT
--- ③
AVG(snow) AS median
FROM OrderSnow
--- ②
WHERE order_id BETWEEN ct/2 AND ct/2 + 1上記クエリを段階を追って解説していきましょう。
①WITH句を使って作成したOrderSnowテーブルのクエリを実行すると、元々のSnowFallテーブルにorder_id列とct列がくっつきます。
新しい列2つは中央値を計算するために後ほど使用します。
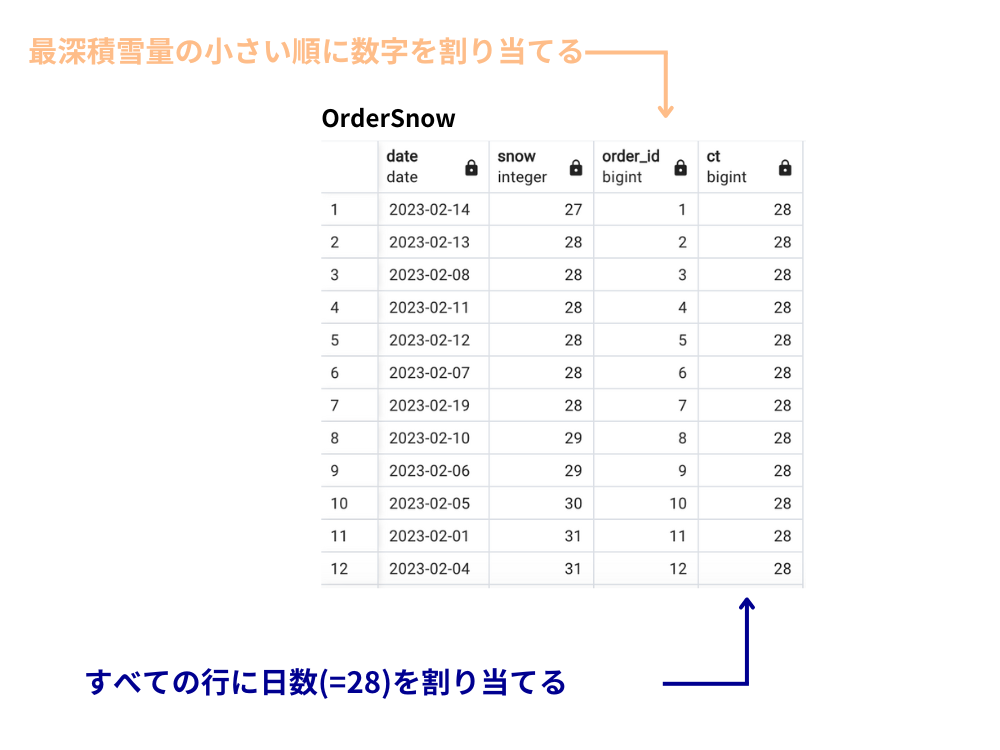
②WHERE句の条件でct列の値(=28)を割った値とその値に1を足した値の間にある数字を算出します。
これはデータ数が偶数であろうが奇数であろうが正しい中央値を求めるためです。
データ数が奇数の場合は真ん中の数字1つが選ばれ、データ数が偶数の場合は真ん中の数字2つが選ばれます。

③ ②で真ん中の数字が1つ選ばれた場合は、AVG(snow)はそのまま選ばれた1つの数字を返します。
②で真ん中の数字が2つ選ばれた場合は、AVG(snow)は選ばれた2つの数字の平均を返します。
これがデータの中央値となるわけです。

まとめ
今回の記事では統計学の超基本、中央値について演習問題つきで解説してみました。
中央値は「まさにデータのど真ん中」を表す指標であるため、分布に偏りがあったり、外れ値があったりと平均値がデータの真ん中として適切ではない時に有用です。
逆に言えば、平均値と中央値に大きな乖離があるときは、データに偏りがあるまたは外れ値がある可能性が高いので、データの分布に立ち返ってみるのが良いでしょう。
当ブログは「世界一分かりやすい解説」を目指しているので、分かりづらい部分があった場合はコメント等で教えていただけると幸いです!
それでは、また次の記事で!



コメント