
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題1「コーシー分布の最尤推定量と標本中央値の比較」の証明について解説していきたいと思います。
今までの章では正規分布や二項分布などの比較的扱いやすい分布に対しての性質を観察してきましたが、本章からはコーシー分布などの比較的扱いづらい分布に対しての性質を考察しています。
本問題を通して、本章で扱ってきたような扱いづらい分布の場合にどのような考察を行うのかについて理解を深めていただけると幸いです!
問題文
<コーシー分布の最尤推定量と標本中央値の比較>
最尤推定量と標本中央値を比較するために
i ) コーシー分布
$$ f_{\theta}(x) = \frac1{\pi(1 + (x-\theta)^2)},~~~~-\infty < x < \infty$$
のフィッシャー情報量$I(\theta)$を求めよ。
標本の大きさ$n$が十分大きい時の$\theta$の最尤推定量$\hat{\theta}_{ML}$の分散$V(\hat{\theta}_{ML})$はいくらか
ii ) 標本の大きさ$n$が十分大きい時の標本中央値$X_{med}$の分散$V(X_{med})$はいくらか
iii ) $V(X_{med})$の$V(\hat{\theta}_{ML})$に対する比を求めよ
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章 演習問題 P228
最尤推定量とは?
最尤推定量とは、未知な母数$\mathbf{\theta} = (\theta_1, \cdots, \theta_n)$を含むような確率分布を尤度$L(\theta)$としたときに、尤度$L(\theta)$を最大にするような$\theta$の値$\tilde{\theta}$のことを指します。
最尤推定量は
$$ \frac\partial{\partial {\theta}}\log L({\theta}) = {0}$$
を解くことによって求めることができます。
フィッシャー情報量$I(\theta)$とは?
フィッシャー情報量とは、誤差${\epsilon}$が正規分布$N(0, \sigma^2)$に従う単回帰モデル${y} = \beta{x} + {\epsilon}$において、データ${y}$の持つ情報量$\frac{{x}'{x}}{\sigma^2}$のことを指す。
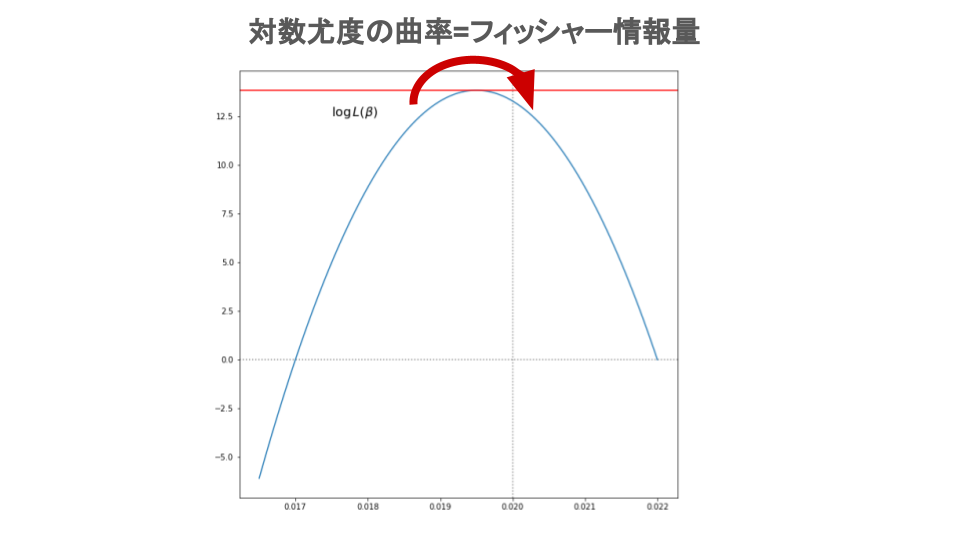
グラフで考えると、単回帰モデル${y} = \beta{x} + {\epsilon}$の対数尤度$L(\beta)$の頂点における曲率(曲がり具合)を指し、フィッシャー情報量が大きいほど曲がり方が急になる、つまり最尤推定量をピンポイントで推定できる(=データ${y}$に対する情報をしっかり持っている)こととなり、フィッシャー情報量が小さいほど山がなだらかになる、つまり最尤推定量を正確には推定できていないことになる。
フィッシャー情報量を求める式は対数尤度の2階微分の期待値$\times(-1)$で求められる。
なお、以下式においてはデータ${y}$が密度関数$f_{\theta}({y})$に従っていることから、尤度$L(\theta) = f_{\theta}(x)$(=確率分布)としている。
$$I(\theta) = – E\left(\frac{\partial^2 \log L(\theta)}{\partial \theta^2}\right) = – E\left(\frac{\partial^2 \log f_{\theta}({y})}{\partial \theta^2}\right) $$
$-1$がかけ算されているのは、フィッシャー情報量が上に凸の曲線の曲率を表すことを示している。
なお、フィッシャーの情報量$I(\theta)$は以下のようにも式変形され、こちらの方が1階微分と2乗で計算できるため、フィッシャーの情報量を求める際には使われることが多い。
$$I(\theta) = – E\left(\frac{\partial^2 \log f_{\theta}({y})}{\partial \theta^2}\right) = E\left( \frac{\partial \log f_{\theta}(y)}{\partial \theta}\right)^2 = \int\left( \frac{\partial \log f_{\theta}(y)}{\partial \theta}\right)^2 f_{\theta}(x) dx$$
解答に向けた準備
本問題を解答するためには、以下の2点について整理しておく必要がある。
- 標本の大きさ$n$が十分に大きい時の最尤推定量$\hat{\theta}_{ML}$の分散$V(\hat{\theta}_{ML})$
- 標本の大きさ$n$が十分に大きい時の標本中央値$\hat{\theta}_{med}$の分散$V(\hat{\theta}_{med})$
標本の大きさ$n$が十分に大きい時の最尤推定量$\hat{\theta}_{ML}$の分散$V(\hat{\theta}_{ML})$
標本の大きさが十分に大きい時は、$\theta$の最尤推定量$\hat{\theta}_{ML}$はほぼ平均$\theta$、分散$\frac1{nI(\theta)}$の正規分布に従う
標本の大きさ$n$が十分に大きい時の標本中央値$\hat{\theta}_{med}$の分散$V(\hat{\theta}_{med})$
観測値の分布が対称であり、標本の大きさが十分に大きい時は、 観測値$X_1,\cdots,X_n$の分布を$g(x)$とすると、$\theta$の標本中央値$X_{med}$は平均が母中央値$\theta$、分散$\frac1{4n\{g(\theta)\}^2}$の正規分布にほぼ従う
解答
それでは、(i)から順に回答をしていきましょう。
コーシー分布のフィッシャー情報量$I(\theta)$と分散V(\hat{\theta}_{ML})$$
コーシー分布$f_{\theta}(x)$の対数尤度は以下のようになる
$$\log f_{\theta}(x) = – \log\pi – \log(1+ (x- \theta)^2)$$
上式を微分すると
$$\frac{\partial \log f_{\theta}}{\partial \theta} = \frac{2(x-\theta)}{1+(x-\theta)^2}$$
よって、フィッシャーの情報量は以下の式で計算される
$$I(\theta) =\int_{\infty}^{\infty} \left(\frac{2(x-\theta)}{1+(x-\theta)^2}\right) \frac1{\pi(1 + (x-\theta)^2)} dx$$
ここで、$x-\theta = y$とすると
$$I(\theta) = \int_{\infty}^{\infty} \frac{4y^2}{\pi(1 + (x-\theta)^2)^3}dy = \frac4\pi \int_{\infty}^{\infty} \left(\frac{1 + y^2}{(1 + y^2)^3} – \frac1{(1 + y^2)^3}\right) dy$$
ここで、$y = \tan\theta$とすると、$\frac1{1 + y^2} = \cos^2 \theta$、$dy = \frac1{\cos^2\theta}d\theta$であり、
積分区間は$-\frac\pi2$から$\frac\pi2$になるので、
$$I(\theta) = \frac4\pi\left(\int_{-\frac\pi2}^{\frac\pi2} \cos^2 \theta d\theta – \int_{-\frac\pi2}^{\frac\pi2} \cos^4 \theta d\theta\right)$$
$\cos^2 \theta$の積分を、2倍角の公式$\cos2\theta = 2\cos^2 \theta -1$を利用して計算すると
$$\int_{-\frac\pi2}^{\frac\pi2} \cos^2\theta d\theta = \frac12\int_{-\frac\pi2}^
{\frac\pi2} \left(\cos2\theta + 1\right)d\theta = \frac12\left[\frac{1}{2}\sin2\theta + \theta\right]^{\frac\pi2}_{-\frac\pi2} = \frac\pi2$$
$\cos^4 \theta$についても同様に計算をすると
$$\int_{-\frac\pi2}^{\frac\pi2} \cos^2\theta d\theta = \frac14\int_{-\frac\pi2}^{\frac\pi2}\left(\cos2\theta + 1\right)^2 d\theta = \frac14\int_{-\frac\pi2}^{\frac\pi2}(\cos^22\theta + 2\cos2\theta + 1)d\theta$$
$$=\frac14\int_{-\frac\pi2}^{\frac\pi2} \cos^2 2 \theta d\theta + \frac14\left[\frac12\sin2\theta + \theta\right]_{-\frac\pi2}^{\frac\pi2} = \frac18\int_{-\frac\pi2}^{\frac\pi2}(\cos4\theta + 1)d\theta + \frac\pi4$$
$$=\frac18\left[\frac14 \sin4\theta + \theta\right]_{-\frac\pi2}^{\frac\pi2} + \frac\pi4 = \frac\pi8 + \frac\pi4 = \frac38\pi$$
よって、
$$I(\theta) = \frac4\pi\left(\frac\pi2 – \frac38\pi\right) = \frac4\pi \times \frac\pi8 = \frac12$$
ここで、標本の大きさ$n$が十分に大きい時、最尤推定量$\hat{\theta}_{ML}$はほぼ平均$\theta$、分散$\frac1{nI(\theta)}$に従うので、
$$V(\hat{\theta}_{ML}) = \frac{1}{n \times \frac12} = \frac2n$$
標本中央値$X_{med}$の分散$V(X_{med})$
$g(x) = f_{\theta}(x)$とおくと、
$$g(\theta) = \frac1{\pi(1 + (\theta-\theta)^2)} = \frac1\pi$$
よって、観測値の分布が対称で、標本$n$が十分大きい時の標本中央値$X_{med}$は平均が母中央値$\theta$、分散が$\frac1{4n\{g(\theta)\}^2}$の正規分布にほぼ従うので、
$$V(X_{med}) = \frac1{4n \times \{\frac1\pi\}^2} = \frac{\pi^2}{4n}$$
$V(X_{med})$の$V(\hat{\theta}_{ML})$に対する比を求めよ
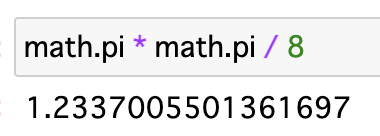
$$\frac{V(X_{med})}{V(\hat{\theta}_{ML})} = \frac{\frac{\pi^2}{4n}}{\frac2n} = \frac{\pi^2}8 = 1.234$$
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題1「コーシー分布の最尤推定量と標本中央値の比較」の証明について解説してみました。
最尤推定量やフィッシャーの情報量などについて解説をし、証明に必要な近似についても解説をしてから、詳細な解答を記述させていただきました。
上記のようにして、正規分布以外においても、標本数が多いという過程を置くことができれば、最尤推定量や標本中央値は正規分布にほぼ従うことを覚えていただけると幸いです。



コメント