
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題3「予測分布, ベータ分布の場合」を非常に簡潔に解説させていただきます。
ベータ分布の性質を知っていれば一瞬で解を求めることができる問題になっているので、「なるほど、ベータ分布にはそんな特性があるのか」という点をご承知おきいたければと思います!
問題文
<予測分布, ベータ分布の場合>
成功$S$, 失敗$F$の二項確率を$P(S)=\theta, P(F)=1-\theta(0\leqq \theta \leqq 1)$としよう。
当初、$\theta$の事前確率分布は一様分布とする。
今、5回目までの逐次の試行結果が$S,F,S,S,S$であったとするとき、6回目の成功、失敗の結果$S,F$の確率分布を、5回目における事後確率分布$Be(5,2)$の密度関数$w(\theta|z)$から
$$\int_0^1 \theta\cdot w'(\theta|z)d\theta, ~~~z=(4,1)$$
によって計算せよ。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第9章 演習問題 P273
ベータ分布とは?
ベータ分布とは、$\alpha$と$\beta$という2つのパラメータによって特徴づけられう分布です。
ベータ分布について3つのトピックスを紹介いたします
- ベータ分布の確率密度関数
- ベータ分布の期待値
- ベータ関数の簡単な計算方法
- ベータ分布と一様分布
順を追って説明いたします
ベータ分布の確率密度関数
ベータ分布の確率密度関数は以下のような式で表されます。
$$f(\theta) = \frac{\theta^{\alpha – 1}(1-x)^{\beta-1}}{B(\alpha, \beta)}$$
ここで、ベータ関数$B(\alpha, \beta)$は次のように計算されます。
$$B(\alpha, \beta) = \int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt$$
ベータ分布の期待値
確率変数$\theta$がベータ分布に従う時、確率分布$\theta$の期待値$E(\theta)$はベータ分布の$Be(\alpha, \beta)$と一致し、
$E(\theta) = \frac\alpha{\alpha + \beta}$
と求められる
ベータ関数の簡単な計算方法
先ほど登場したベータ関数$B(\alpha, \beta)$は$\alpha, \beta$が自然数なら次のように計算することができます
$$B(\alpha, \beta) = \frac{(\alpha -1)! (\beta – 1)!}{(\alpha + \beta -1)!}$$
ベータ分布と一様分布
ベータ分布$Be(\alpha, \beta)$に$\alpha = 1, \beta = 1$を代入すると、
$$Be(1,1) = \frac{\theta^0 (1-\theta)^0}{B(1,1)} $$
ここで、$B(1,1) = \frac{0!0!}{(2-1)!} = 1$であるから、
$$Be(1,1) = \frac11 = 1$$
これは一様分布の確率密度関数に他ならない。
よって、一様分布というのは、ベータ分布の$\alpha$と$\beta$が1であるような時の分布のことをいう。
尤度関数が二項分布、事前確率分布がベータ分布である時の事前確率分布の更新
尤度関数($\fallingdotseq$条件付き確率)が二項分布であり、事前確率分布がベータ分布であるような時について考えます。
$n$回中$x$回成功するという状況における尤度関数・二項分布の式は
$$f(x|\theta) = {}_n\mathrm{C}_x \theta^x (1-\theta)^{n-x}$$
であり、同様に事前確率分布$w(\theta) = Be(\alpha, \beta)$の式は
$$w(\theta) = \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)}$$
である。
ここで、事後確率分布$w'(\theta)$を求める式は
$$w'(\theta) = \frac{w(\theta_i)\cdot f(z|\theta_i)}{\sum w(\theta_i)\cdot f(z|\theta_i)}$$
で求められるので、$w(\theta_i)$と$f(z|\theta_i)$のそれぞれにベータ分布と二項分布の式を代入し整理すると
$$w'(\theta) \propto \theta^{\alpha + x – 1}(1-\theta)^{\beta + (n-x) -1} \sim Be(\alpha + x, \beta + (n-x))$$
これは、成功の場合はベータ分布の左側$x$が$+1$され、失敗の場合はベータ分布の右側$n-x$が$+1$されることを意味する。
よって、尤度関数が二項分布、事前確率分布がベータ分布であるような場合には、成功または失敗という結果を得るために、ベータ分布に数字が追加される形で事後分布(=次の施行の事前分布)が更新されることを意味する。
この時、事前確率分布ベータ分布が更新されることによって、次の事後確率の期待値が変動する、というところが本問題の肝になっております。
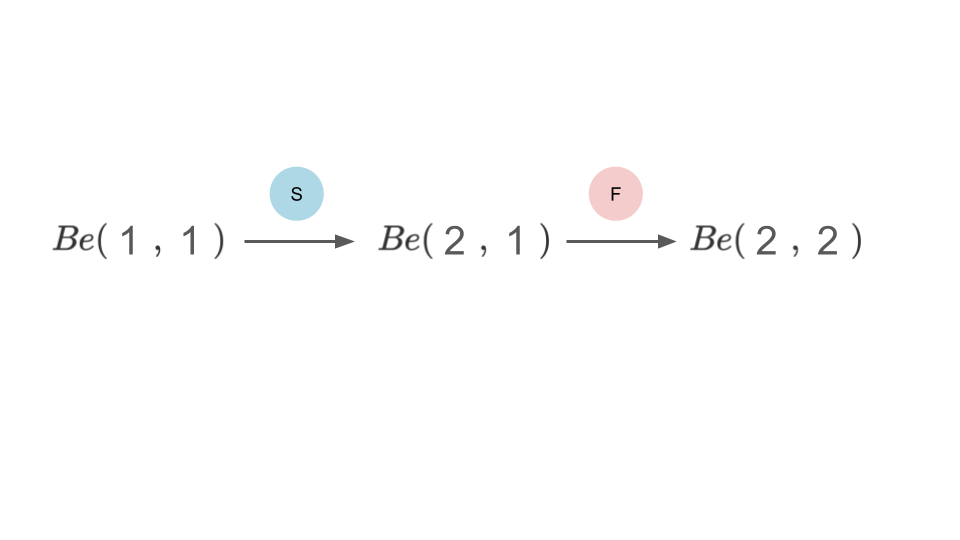
解説
本問題は上記Pointの内容を踏まえると、非常にシンプルに6回目の成功$S$、失敗$F$の確率を求めることができます。
本問題の前提の確認
本問題では以下の3つの前提が置かれています。
- 尤度関数は二項分布
- 事前確率分布は一様分布、つまりベータ分布$Be(1,1)$
- 5回目のまでの試行結果は$S,F,S,S,S$、つまり6回目の事前確率分布は$Be(5,2)$
そして、6回目の成功確率を考えることは、5回目の事前確率分布$Be(5,2)$を利用すれば、6回目に成功が出る期待値を求めることと同じであることが分かります。
ここで、事前確率分布$Be(5,2)$の期待値は次のようにして求められます。
$$Be(5,2)の期待値 = \frac{5}{5+2} = \frac57$$
よって、求める6回目の成功確率、失敗確率は
$$成功確率 = \frac57$$
$$失敗確率 = 1-\frac57 = \frac27$$
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題3「予測分布, ベータ分布の場合」を非常に簡潔に解説させていただきました!
とはいえ、問題を解く前提となるベータ分布に関するインプットがたくさん必要で大変だったかと思われます。
とはいえ、尤度関数が二項分布を仮定できるような状況では、事前確率分布をベータ分布と置くことができれば、事後確率分布の更新が非常に簡単にできることを体験いただけたかと思います!
皆さんもぜひ尤度関数が二項分布の場合には、本記事で紹介した方法を使って事後確率分布を逐次的に更新してみてください!



コメント