
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、KaggleのThe Learning Agency Lab – PII Data Detectionコンペにおいて、ビタビアルゴリズムを実装してみた時のロジックを、図解しながら解説していきたいと思います。
大規模言語モデル入門の第6章の内容を参考にしながら実装しましたが、ところどころ理解が及ばない部分があり、コンペに一緒に参加した仲間に説明できなかったことが動機となって、今回このような解説記事を書いた次第です。
できる限り分かりやすく解説していきますが、分かりずらい箇所があった場合にはコメント等をいただければ追加説明等を付与いたしますので、お気軽にコメントいただけると幸いです。
ビタビアルゴリズムの概要
ビタビアルゴリズムについて、Wikipediaの説明を引用してみます。
ビタビアルゴリズム(英: Viterbi algorithm)は、観測された事象系列を結果として生じる隠された状態の最も尤もらしい並び(ビタビ経路と呼ぶ)を探す動的計画法アルゴリズムの一種であり、特に隠れマルコフモデルに基づいている。
https://ja.wikipedia.org/wiki/%E3%83%93%E3%82%BF%E3%83%93%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0
隠れマルコフモデルについて理解を深めるためにまずは「マルコフ過程」「マルコフ連鎖」という単語について理解を深めましょう。
マルコフ過程
マルコフ過程(マルコフかてい、英: Markov process)とは、マルコフ性をもつ確率過程のことをいう。すなわち、未来の挙動が現在の値だけで決定され、過去の挙動と無関係であるという性質を持つ確率過程である。
https://ja.wikipedia.org/wiki/%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95%E9%81%8E%E7%A8%8B
「未来の挙動が現在の値だけで決定される」というところがポイントです。
イメージとしては、天気で考えてみると分かりやすいかもしれません。
1日おきの天気を考えてみると
「今日晴れだった場合は明日も晴れであることが多い」
「晴れから急に雨になることはあまりない」
「晴れから曇りになることや、曇りから雨になることは比較的多い」
などの経験則があるかと思われます。
一方で、昨日や一昨日の天気というのは、今日の天気以上に明日の天気に影響を及ぼすということは(梅雨などの雨フィーバーボーナスタイムを除けば)ほとんどないはずです。
このように、未来の挙動が過去の挙動と無関係であることをマルコフ性と言います。
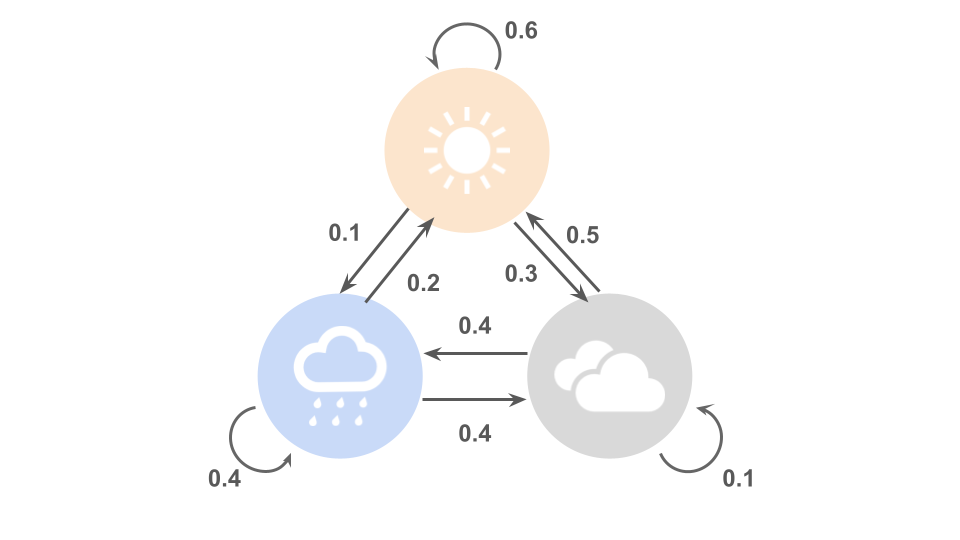
つまり、以下の図のように、明日の天気というのは今日の天気がどうであったかによって、確率的にある天気に推移するものと考えられます。
このように、ある状態(=天気)からある状態への移る際の確率を遷移確率と呼びます。
マルコフ連鎖
マルコフ連鎖(マルコフれんさ、英: Markov chain)とは、確率過程の一種であるマルコフ過程のうち、とりうる状態が離散的(有限または可算)なもの(離散状態マルコフ過程)をいう。
https://ja.wikipedia.org/wiki/%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95%E9%80%A3%E9%8E%96
例えば、先ほどの例のように「今日」「明日」や「1日後」「2日後」のような少し飛び飛びの値のことを離散的と呼びます。
つまり、先ほどの天気のような例はマルコフ過程でもありマルコフ連鎖でもあるということができます。
隠れマルコフモデル
隠れマルコフモデル(かくれマルコフモデル、英: hidden Markov model; HMM)は、確率モデルのひとつであり、観測されない(隠れた)状態をもつマルコフ過程である。
https://ja.wikipedia.org/wiki/%E9%9A%A0%E3%82%8C%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95%E3%83%A2%E3%83%87%E3%83%AB
先ほどの例では、今日の天気や明日の天気は観測可能だったので、今日の天気という情報をもとに明日の天気を確率的にある程度予測することができました。
一方で、隠れマルコフモデルというのは「状態(=天気)」が見えないようなマルコフモデルのことを指します。
「じゃあ、今の状態が見えないのにどうやって次の状態を予測すればいいのさ」と思われたことでしょう。
この時、我々に与えられるのは今の「状態」ではなく、「出力」というものが与えられます。
天気の例で言えば、「朝ランニングをしている人」などが「出力」として考えられます。
隠れている状態が晴れの場合はそこそこ多くの人が朝ランニングをしているかもしれません。
曇りの場合は晴れの時よりも涼しいのでより多くの人がランニングをしているかもしれません。
一方で、雨の場合はコンディションが悪いため、朝ランニングをしている人は他の天候の日に比べて少ないかもしれません。
そして皆さんには今日の天気という情報は渡されていないが、今日の朝ランニングをしていた人数だけが情報として与えられている状況で、「明日の天気を予測してください」と言われてしまうのが隠れマルコフモデルということができます。
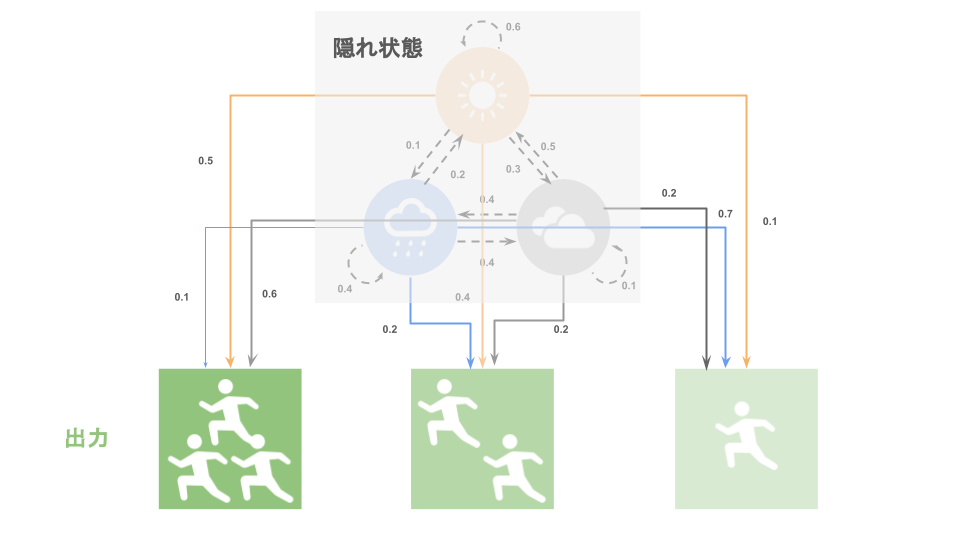
そして、「雨の日の場合はどれだけの確率で多くの人が朝ランニングをするのか」のように、隠れている状態から出力が導かれる確率を「出力確率」と呼びます。
ビタビアルゴリズム
ビタビアルゴリズム(英: Viterbi algorithm)は、観測された事象系列を結果として生じる隠された状態の最も尤もらしい並び(ビタビ経路と呼ぶ)を探す動的計画法アルゴリズムの一種であり、特に隠れマルコフモデルに基づいている。
https://ja.wikipedia.org/wiki/%E3%83%93%E3%82%BF%E3%83%93%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0
さて、先ほどの例で、ある地域における過去3日間の朝ランニング人口について、
「多い」→「普通」→「多い」
という変遷を経ていたことがわかったとしましょう。
この時の過去3日間の天気として、最もありそう(=尤もらしい)なのはどのような天気の組み合わせでしょうか。
ランニング人口が比較的多い日が2日あるということは、ずっと曇りだったのかもしれません。
もしかしたら、曇り→晴れ→曇りで中日は暑かったから人が減ったのかもしれません。
もしかしたら、曇り→雨→曇りで、中日は雨が降ったから人がランニングする人が減少したのかもしれません。
このように、ありうる天気のパターンは無数に考えられますが、遷移確率、出力確率を用いて、さまざまなパターンを試しながら(=動的計画法)、一番ありそうなパターンを導くのがビタビアルゴリズムになります。

PII-Detectionコンペの概要
ビタビアルゴリズムの実装について紹介する前に、今回ビタビアルゴリズムを導入したPII-Detectionコンペについて簡単に説明をしておきましょう。
PII-Detection(個人情報検出)コンペとは、文章中に個人情報があった場合、その個人情報が氏名なのかURLなのか住所なのか等の情報をラベリングするコンペティションです。
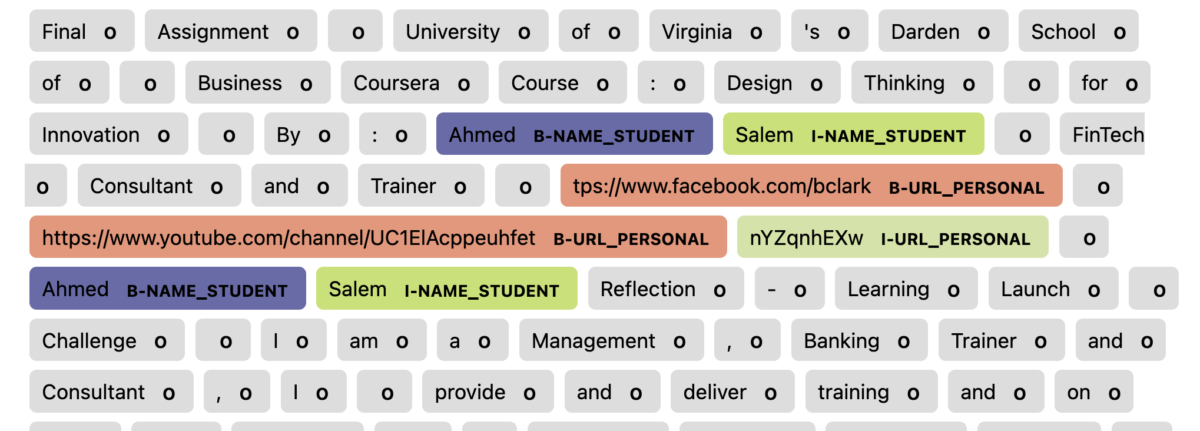
上記図にもあるように、連続するPIIのうち、1つ目のPIIには「B-」のラベルを、2つ目以降のPIIラベルには「I-」のラベルを付与することとします。
そして、今回このコンペディションでビタビアルゴリズムを実装する意義は「B-ラベルとI-ラベルのルールに反するラベルを排除する」ことです。
例えば、「I-NAME_STUDENT」ラベルの次に「I-URL_PERSONAL」ラベルが来ることは上記ルールからすると誤りになります。
このような「尤もらしくない」ラベルをビタビアルゴリズムによって排除したい、というのがビタビアルゴリズム導入の動機です。
ビタビアルゴリズムの実装部分
それでは、実際のビタビアルゴリズム実装部分を抜粋してみていきましょう。
ビタビアルゴリズムの実装には、create_transitions関数とdecode_with_viterbi関数の2つの関数を用います。
def create_transitions(
label2id: dict[str, int]
) -> tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
"""遷移スコアを定義"""
### B-ラベルIDのlist
b_ids = [v for k, v in label2id.items() if k[0] == 'B']
### I-ラベルIDのlist
i_ids = [v for k, v in label2id.items() if k[0] == 'I']
o_id = label2id['O']
# 開始遷移スコアを定義する
# 全てのスコアを-100で初期化する
start_transitions = torch.full([len(label2id)], -100)
# B-ラベル/O-ラベルへは遷移可能として0を代入
start_transitions[b_ids] = 0
start_transitions[o_id] = 0
# ラベル間の遷移スコアを定義する
# 全てのスコアを-100で初期化
transitions = torch.full([len(label2id), len(label2id)], -100)
# B-ラベル/O-ラベルは全てのラベルから遷移可能
transitions[:, b_ids] = 0
transitions[:, o_id] = 0
# I-から同じタイプのI-への遷移可能として0を代入
transitions[i_ids, i_ids] = 0
#遷移スコアdfを定義
df = pd.DataFrame(transitions)
df.columns = label2id.keys()
df.index = label2id.keys()
# B->Iの変換の作成
cols = ['ID_NUM', 'NAME_STUDENT', 'PHONE_NUM', 'STREET_ADDRESS', 'URL_PERSONAL']
for col in cols:
df.at[f'B-{col}', f'I-{col}'] = 0
display(df)
# テンソルに変換
transitions = torch.tensor(np.array(df.astype('f')))
# 終了遷移スコアを定義する
# 全てのライベルから遷移可能
end_transitions = torch.zeros(len(label2id))
return start_transitions, transitions, end_transitions
def decode_with_viterbi(
predictions: torch.Tensor,
start_transitions: torch.Tensor,
transitions: torch.Tensor,
end_transitions: torch.Tensor
) -> torch.Tensor:
"""ビタビアルゴリズムを用いて最適なラベル列を探索"""
# バッチサイズ、 系列長(トークンの長さ)を取得する
batch_size, seq_length, _ = predictions.shape
# 予測スコアに関して、0次元目と1次元目を入れ替える
# 予測スコアは系列長 * バッチサイズ * ラベル数になる
predictions = predictions.transpose(1,0)
histories = [] # 最適ラベル保存のためのarray
# 開始遷移スコアと予測スコアを加算して、累積スコアの初期値とする
score = start_transitions + predictions[0]
for i in range(1, seq_length): # 系列長でForを回す(初期値0時点は入っているので1からスタート)
# 累積スコアを3次元に変換する
broadcast_score = score.unsqueeze(2)
# 現在の予測スコアを3次元に変換する
broadcast_prediction = predictions[i].unsqueeze(1)
# 累積スコアと遷移スコアと現在の予測スコアを加算して、現在の累積スコアを取得する
next_score = (
broadcast_score + transitions + broadcast_emission
)
# 現在の累積スコアの各ラベルの最大値とそのインデックスを取得する = 最も確率が高い経路を辿るための準備
next_score, indices = next_score.max(dim = 1)
# マスクしない要素の場合、累積スコアを更新する
score = next_score
# スコアの高いインデックスを履歴のlistに追加する
histories.append(indices)
# 終了遷移スコアを加算して合計スコアとする
score += end_transitions
# 各事例で最適なラベル列を取得する
best_labels_list = []
for i in range(batch_size):
# 合計スコアの中で最大のスコアとなるラベルを取得する = 遷移確率を加味した時に最もありうるラベル
_, best_last_label = score[i].max(dim=0)
best_labels = [best_last_label.item()]
# 再度のラベルの遷移を逆方向に探索し、最適なラベル列を取得する
for history in reversed(histories): # これで一番最後から辿れる
best_last_label = history[i][best_labels[-1]] #iバッチ目の(最も遷移確率の高い)ラベルを逆から見ていく
best_labels.append(best_last_label.item())
# 順序を反転する
best_labels.reverse()
best_labels_list.append(best_labels)
return torch.LongTensor(best_labels_list)
# 遷移行列の作成
start_transitions, transitions, end_transitions = (
create_transitions(label2id)
)
predictions = trainer.predict(ds).predictions
predictions = softmax(predictions, axis = -1)
# ビタビアルゴリズムのためにテンソルに変換
predictions = torch.Tensor(predictions)
pred_label_ids = decode_with_viterbi(
predictions,
start_transitions,
transitions,
end_transitions
)
...コード解説: 遷移スコア作成
まずは、create_transitions関数について解説をしていきます。
create_transitions
create_transitions関数ではのちに用いる遷移スコアと呼ばれるものを表の形式で算出していきます。
これは、遷移確率を計算する代わりに「このラベルからこのラベルへの遷移は絶対にあり得ない」ような遷移に対してペナルティを与えるようなスコアになります。
ペナルティを与えるとどうなるかというと、最終的には各遷移スコアを合計して最もスコアの高い、つまり最もあり得そうなラベルの組み合わせを選出するのですが、その点については後ほど解説いたします。
今回作成する遷移スコアは以下の3種類です。
- 開始遷移スコア(start_transitions)
- ラベル間の遷移スコア(transitions)
- 終了遷移スコア(end_transitions)
それぞれの遷移スコアについて見ていく前に、コードに度々登場するlabel2idについて紹介いたしましょう。
label2id
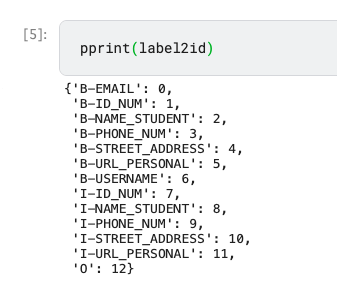
label2idとは、「B-」ラベルや「I-」ラベル、そして何もPIIが検出できなかった時の「O」ラベルをID番号に変換するためのdict形式の対応表です。
label2idを出力してみると、各ラベルに対応する数字(ID)が割り当てられていることがわかるかと思います。
開始遷移スコア(start_transitions)
開始遷移スコアは文章の一番初めのラベルに対する遷移スコアになります。
天気の例で言えば、「晴れ」→「雨」→「曇り」という並びであった場合の「晴れ」に対する遷移スコアです。
天気の場合はどんな天気でも一番初めに来ることはありますが、PII-Detectionにおいてはそうではありません。
なぜなら、PIIラベルには「B-」というラベルの始まりを意味するラベルと、そのラベルの続きのラベルであることを意味する「I-」というラベルが存在するためです。
そのため、「I-」というラベルでいきなりスタートすることはあり得ません。
そのため、start_transitionsでは「I-」ラベルに対して、$-100$というペナルティを与えることで、「I-」ラベルが最初に来るようなラベルの組み合わせが選ばれないようにします。
start_transitionsを作成しているコードは以下の部分になります。
def create_transitions(
label2id: dict[str, int]
) -> tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
"""遷移スコアを定義"""
### B-ラベルIDのlist
b_ids = [v for k, v in label2id.items() if k[0] == 'B']
### I-ラベルIDのlist
i_ids = [v for k, v in label2id.items() if k[0] == 'I']
o_id = label2id['O']
# 開始遷移スコアを定義する
# 全てのスコアを-100で初期化する
start_transitions = torch.full([len(label2id)], -100)
# B-ラベル/O-ラベルへは遷移可能として0を代入
start_transitions[b_ids] = 0
start_transitions[o_id] = 0上記コードによって、以下のようなstart_transitionsが作成されます。

配列の出力だけではわかりづらいので、この配列をデータフレームに格納して、インデックスをつけてみると以下のようになります。
tmp_df = pd.DataFrame(start_transitions)
tmp_df.index = label2id.keys()
tmp_df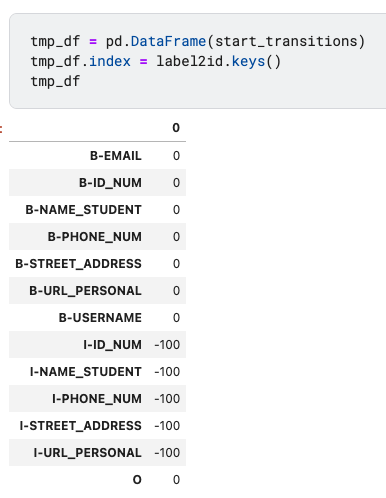
終了遷移スコア(end_transitions)
終了遷移スコアも、開始遷移スコアと同じように「文章の終わりにこのラベルは来ないよね」というものにペナルティを与えるようなスコアになります。
とはいえ、今回のPIIコンペにおいては全てのラベルが文章の一番最後に来る可能性があるので、end_transitionsとしてはラベル数分の0が入った配列を用意することとなります。
def create_transitions(
label2id: dict[str, int]
) -> tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
"""遷移スコアを定義"""
...
# 終了遷移スコアを定義する
# 全てのラベルから遷移可能
end_transitions = torch.zeros(len(label2id))
return start_transitions, transitions, end_transitionstmp_df = pd.DataFrame(end_transitions)
tmp_df.index = label2id.keys()
tmp_df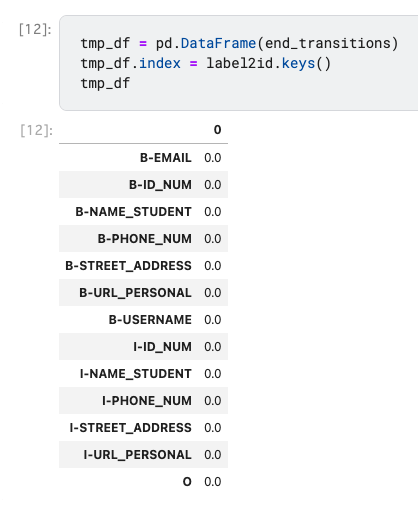
ラベル間遷移スコア(transitions)
ラベル間の遷移スコアについては以下のような条件が必要になります。
- B-ラベルとOラベルは全てのラベルから遷移可能
- IラベルからIラベルへの移動はタイプが同じであれば遷移可能
- BラベルからIラベルへの移動はタイプが同じであれば遷移可能
以上の条件を加味して遷移スコアを作成するコードは以下の部分になります。
def create_transitions(
label2id: dict[str, int]
) -> tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
"""遷移スコアを定義"""
### B-ラベルIDのlist
b_ids = [v for k, v in label2id.items() if k[0] == 'B']
### I-ラベルIDのlist
i_ids = [v for k, v in label2id.items() if k[0] == 'I']
o_id = label2id['O']
# ラベル間の遷移スコアを定義する
# 全てのスコアを-100で初期化
transitions = torch.full([len(label2id), len(label2id)], -100)
# 条件1: B-ラベル/O-ラベルは全てのラベルから遷移可能
transitions[:, b_ids] = 0
transitions[:, o_id] = 0
# 条件2: I-から同じタイプのI-への遷移可能として0を代入
transitions[i_ids, i_ids] = 0
#遷移スコアdfを定義
df = pd.DataFrame(transitions)
df.columns = label2id.keys()
df.index = label2id.keys()
# 条件3: B->Iの変換の作成
cols = ['ID_NUM', 'NAME_STUDENT', 'PHONE_NUM', 'STREET_ADDRESS', 'URL_PERSONAL']
for col in cols:
df.at[f'B-{col}', f'I-{col}'] = 0
display(df)
# テンソルに変換
transitions = torch.tensor(np.array(df.astype('f')))
...上記コードで作成したラベル間の遷移スコアは以下のようになっています。
display(transitions)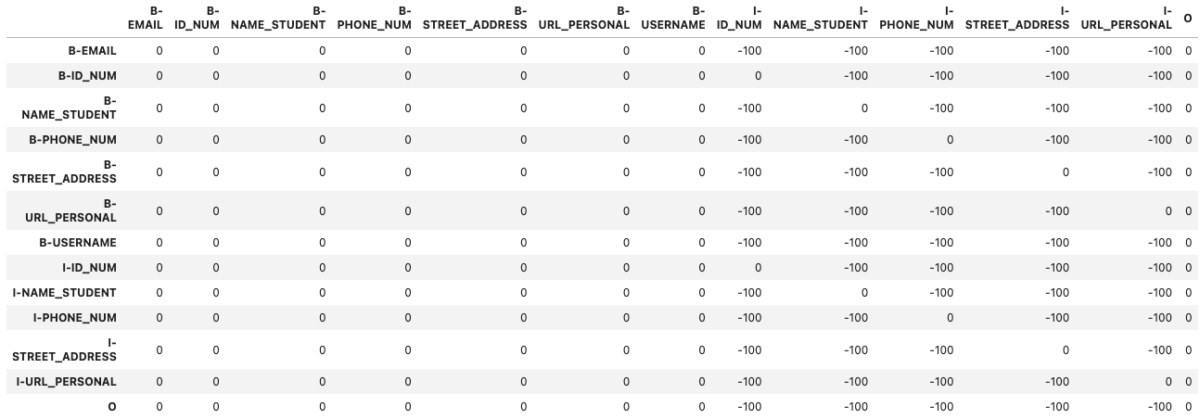
このようにして開始時、ラベル間、終了時の3パターンの遷移スコアを作成することができました。
次にビタビアルゴリズムを実際に行う部分のコードを見ていきます。
コード解説: ビタビアルゴリズム実行部分
ビタビアルゴリズム実行部分については3つのステップに分けて見ていきます。
- 下準備
- スコア計算
- 最適なラベル順の再現
上記3ステップについて解説する前に、前提となる今回のモデルの予測値predictionsがどのような形で出力されるのかを見ていきましょう。
予測値predictionsの形式
学習データを用いて訓練されたモデルはラベルの予測値predictionsを以下のような次元の構成で出力します。
- バッチサイズ : PIIを予測するドキュメントの数
- 系列長 : 1ドキュメントあたりのトークンの数
- ラベル数: B- / I- / Oラベルの数
図にすると以下のように3次元構造になっています。
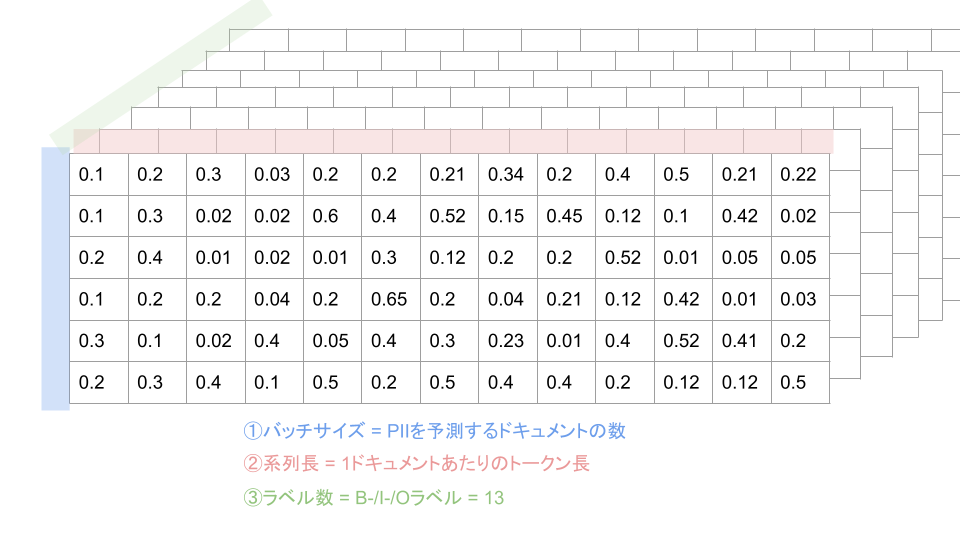
この時、各セルに入っている値はラベルの予測確率です。
つまり、1次元(何番目のドキュメントか)と2次元(ドキュメントの何個目のトークンか)を固定して3次元目を並べて見たときに、最も値の大きい=最も確率の高いラベルが選ばれるわけです。
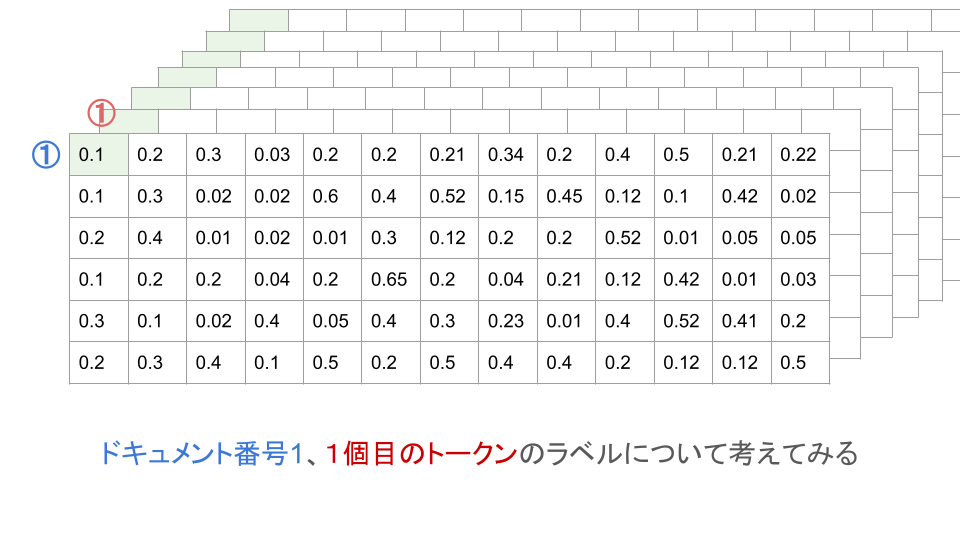

ですが、上記のラベルの選択法では、ラベルの文脈、つまり前後のラベルが何であったのかについては考慮されていません。
そのため、ビタビアルゴリズムを使用して前後のラベルも考慮した最も可能性の高いラベルを推定しようというのが当該アルゴリズム導入の動機です。
predictionsがこのような形であることを踏まえて、ビタビアルゴリズムの実装を順に見ていきましょう。
下準備
ビタビアルゴリズムの下準備の段階では以下の3つのことを実行します。
- バッチサイズと系列長を取得する
- 予測スコアの次元を①バッチサイズ、②系列長、③ラベル数から①系列長、②バッチサイズ、③ラベル数に変更する
- 遷移スコアの初期値を設定する
バッチサイズと系列長を取得する
def decode_with_viterbi(
predictions: torch.Tensor,
start_transitions: torch.Tensor,
transitions: torch.Tensor,
end_transitions: torch.Tensor
) -> torch.Tensor:
"""ビタビアルゴリズムを用いて最適なラベル列を探索"""
# バッチサイズ、 系列長(トークンの長さ)を取得する
batch_size, seq_length, _ = predictions.shape まずは、モデルの予測結果からバッチサイズ(PIIラベルを予測する文の数)と系列長(文のトークンの長さ)を取得します。
先ほどの図でいう1次元目(縦)と2次元目(横)にあたります。
予測スコア(predictions)の次元を①バッチサイズ、②系列長、③ラベル数から①系列長、②バッチサイズ、③ラベル数に変更する
# 予測スコアに関して、0次元目と1次元目を入れ替える
# 予測スコアは系列長 * バッチサイズ * ラベル数になる
predictions = predictions.transpose(1,0)最初の並びは1次元目にバッチサイズが来ていますが、今回のビタビアルゴリズムにおいては系列長の最初から最後に向かって順番に処理していく必要があるため、1次元目に系列長が来るように順番を並び替えます。
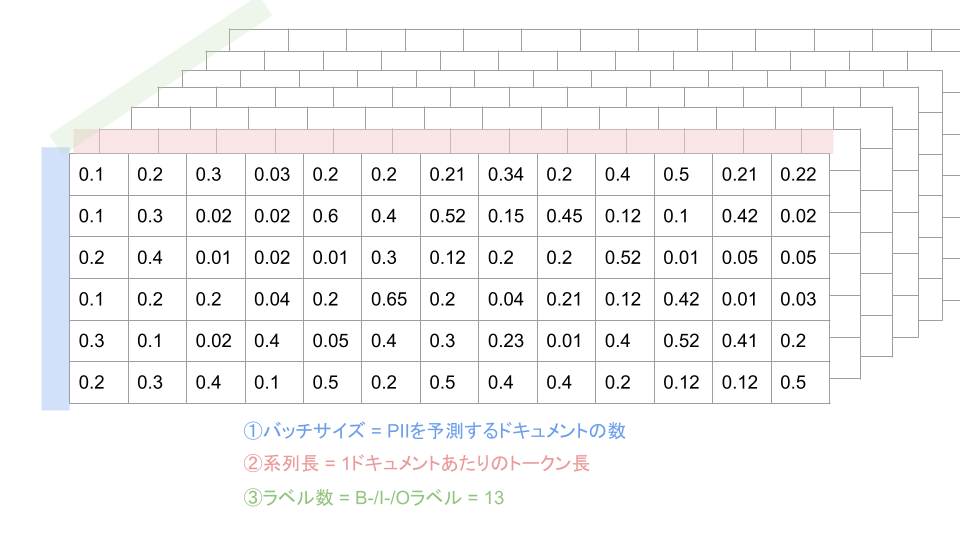

遷移スコアの初期値を設定する
# 開始遷移スコアと予測スコアを加算して、累積スコアの初期値とする
score = start_transitions + predictions[0] 下準備の最後に遷移スコアの初期値を設定します。
この初期値は開始時遷移スコアstart_transitionsと系列長1個目のドキュメントごとのラベル確率predictions[0]に基づいて計算されます。
predictions[0]は下図の赤い部分にあたります。

開始遷移スコアstart_transitionsはラベルの数と同じ13個の数字(0か-100か)を格納した配列なので、predictions[0]の各ドキュメントのラベル確率に一律に足し算される結果となります。

これによって、系列の一番初めにI-ラベルが来る確率はグッと小さくなります。
これで下準備の工程は終了です。
次にビタビアルゴリズムのスコア計算部分を見ていきましょう。
スコア計算
スコア計算については、以下の4つの手順を系列長の2番目から最後まで実施していくこととなります。
- 累積スコアと次の予測値の次元を整える
- 累積スコアとラベル間遷移スコアと次の予測スコアを足し算する
- 現時点での最もスコアの高いラベル位置を記憶し、累積スコアをスコア最大値に更新する
- スコアの高かったラベル位置を履歴historyとして残す
- 系列の一番最後に終了遷移スコアを足す
ここはビタビアルゴリズムのかなり難しい部分になってくるので、順を追って読み解いていきましょう。
累積スコアと次の予測値の次元を整える
for i in range(1, seq_length): # 系列長でForを回す(初期値0時点は入っているので1からスタート)
# 累積スコアを3次元に変換する
broadcast_score = score.unsqueeze(2)
# 現在の予測スコアを3次元に変換する
broadcast_prediction = predictions[i].unsqueeze(1)ここで先ほど赤い2次元の配列だったscoreに3次元目を追加していきます。
そして、次の予測値predictions[i]の方には、なんと2次元目を追加していき、こちらも結果として3次元になります。
そのため、3次元の累積スコアbroadcast_scoreと3次元の予測スコアbroadcast_predictionは同じ3次元でも次元ごとの大きさが異なります。
例えば、バッチサイズ(=ドキュメント数)が10、ラベル数が13とすると
broadcast_scoreは3次元目に次元が追加されているので、10 * 13 * 1の配列となります。
一方で、broadcast_predictionは2次元目に次元が追加されているので、10 * 1 * 13の配列となります。
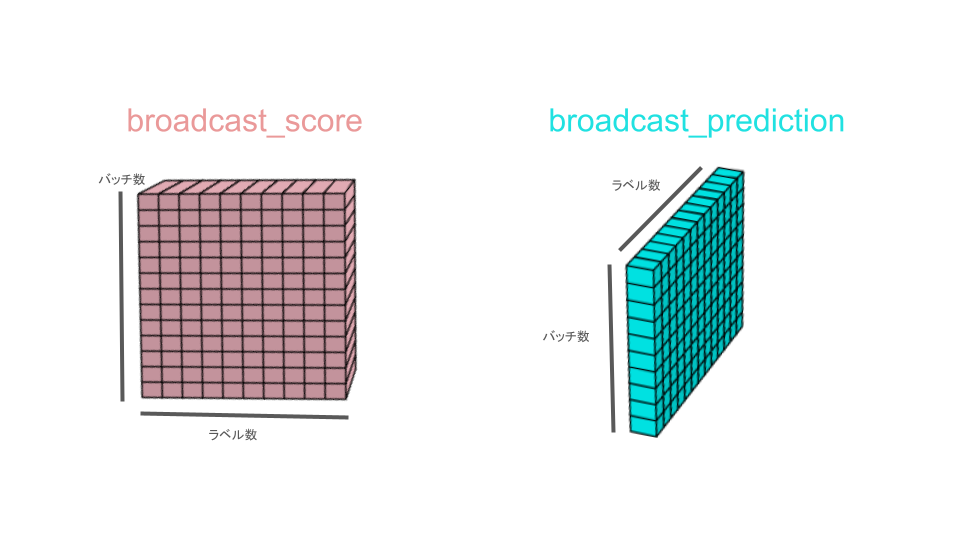
累積スコアとラベル間遷移スコアと次の予測スコアを足し算する
# 累積スコアと遷移スコアと現在の予測スコアを加算して、現在の累積スコアを取得する
next_score = (
broadcast_score + transitions + broadcast_emission
)先ほど作成した累積スコアbroadcast_scoreと予測スコアbroadcast_predictionとラベル遷移スコアtransitionsを足し算します。
この手順についてもさらに2ステップに分解して見ていきましょう
- broadcast_score + transitions …(*)
- (*) + broadcast_prediction
broadcast_score + transitions
累積スコアbroadcast_scoreはバッチ数 * ラベル数 * 1の3次元配列です。
一方で、ラベル遷移スコアtransitionsはラベル数 * ラベル数の2次元配列です。
この時、ラベル遷移スコアtransitionsの1次元目には現在のラベルがインデックスとしてあり、2次元目には次のラベルがカラム名として存在しています。
そして、現在のラベルから次のラベルへの遷移について、実際にはあり得ないような遷移については-100という数字が設定されています。

累積スコアbroadcast_score(バッチ数 * ラベル数 * 1)とラベル遷移スコアtransitions(ラベル数 * ラベル数)を足し算するとどのような配列ができるのでしょうか?
答えはバッチ数 * ラベル数 * ラベル数のような配列が出来上がります。
イメージとしては、broadcast_scoreが3次元方向にラベル数分複製され、バッチ数 * ラベル数 * ラベル数の3次元配列になってから、ラベル数 * ラベル数の部分にラベル遷移スコアtransitionsがバッチ数分だけ足し算されるイメージです。
これによって、現在のラベルからあり得ないラベルに遷移する時のスコアに罰則を与えることができます。
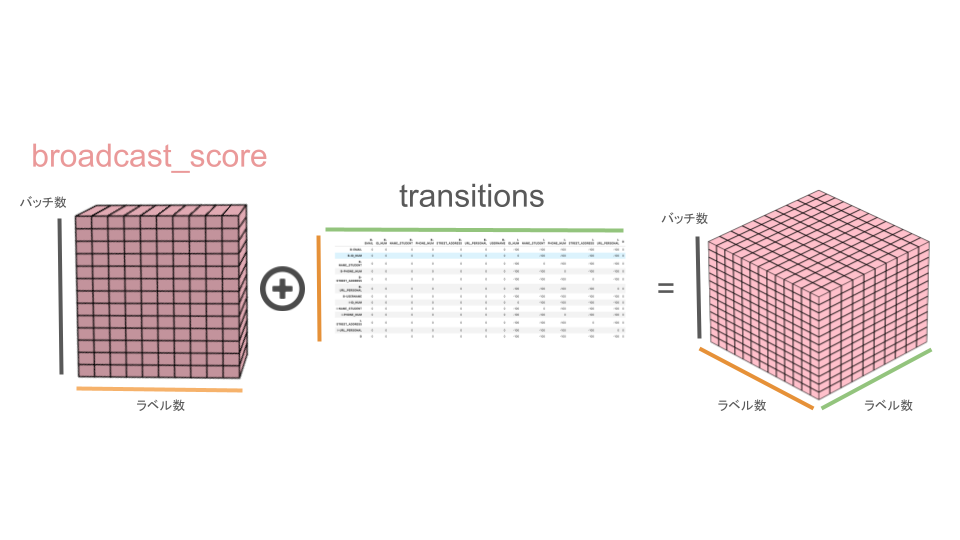
(*) + broadcast_prediction
次に、この先ほどの足し算の結果出来上がったバッチ数 * ラベル数 * ラベル数の立体(*)に、次の予測スコアbroadcast_prediction(バッチ数 * 1 * ラベル数)を足し算していきます。
さて、今回のような次元数は同じでも各次元の値が異なる場合にはどのように足し算がなされるのでしょうか。
次の予測スコアbroadcast_predictionの2次元目が立体(*)と比較して不足しているので、次の予測スコアbroadcast_predictionの2次元目を増やすような形をとります。
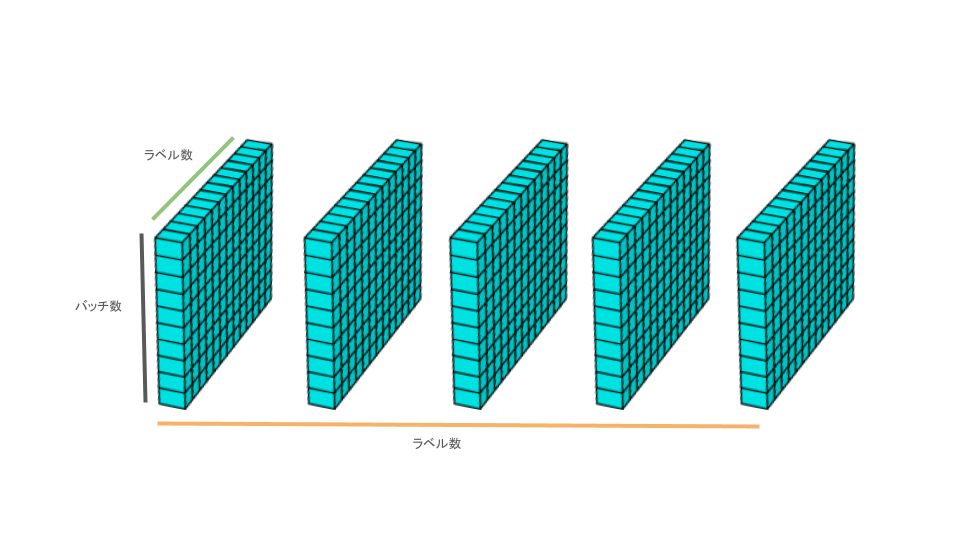
そして、2次元目を複製したbroadcast_predictionと立体(*)を足し合わせることとなります。
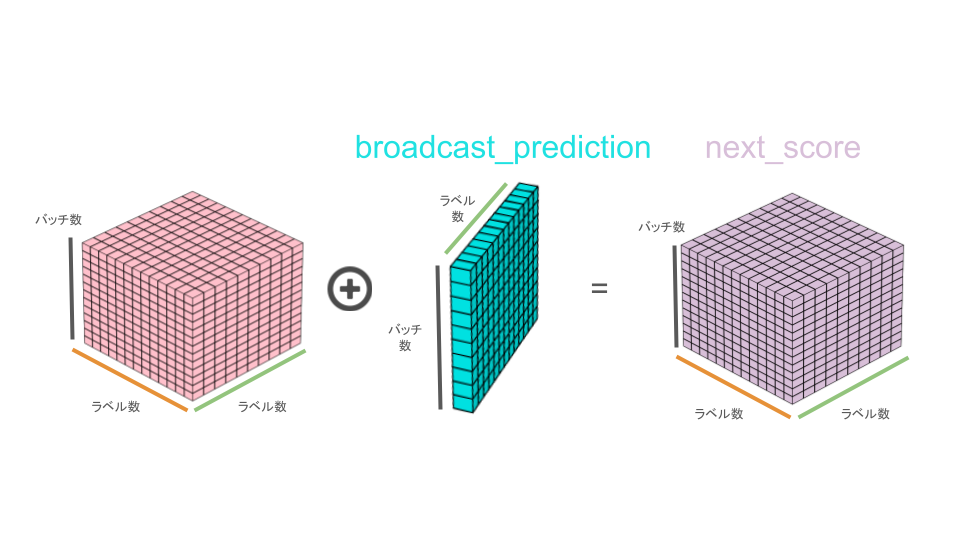
上記の処理で、罰則を加味した現在ラベル(2次元方向)に対する次のラベルのスコア(3次元方向)が算出できたことになります。
現時点での最もスコアの高いラベル位置を記憶し、累積スコアをスコア最大値に更新する
# 現在の累積スコアの各ラベルの最大値とそのインデックスを取得する = 最も確率が高い経路を辿るための準備
next_score, indices = next_score.max(dim = 1)ここまでで現在ラベルに対する次ラベルの罰則付きスコアを算出してきましたが、次の処理では現在ラベルスコアのうち、最もスコアの高い(現時点で最もあり得る)ラベルを抽出していきます。
ここで、現在ラベルスコアのうちの最大値を取る、というところに注意が必要です。
つまり、「次ラベルがI-NAME_STUDENTラベルなら、現在のラベルがB-URL_PERSONALなわけないね」という、次から現在最もありうるラベルを逆算するような選択の仕方をします。
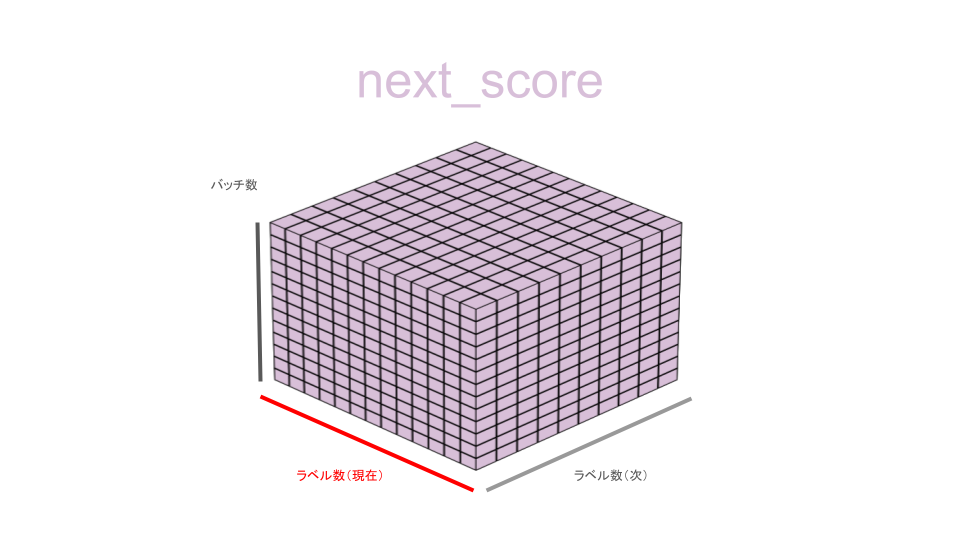

そして最大スコアを取得すると同時に、最大スコアであったラベルが何であったのかをindicesに情報として格納しています。
スコアの高かったラベル位置を履歴historyとして残す
# スコアの高いインデックスを履歴のlistに追加する
histories.append(indices)前の手順で最もスコアの高かったラベル位置をhistoryに格納します。
historyに格納したラベル情報はスコア計算後の次の手順で活用します。
系列の一番最後に終了遷移スコアを足す
# 終了遷移スコアを加算して合計スコアとする
score += end_transitionsループ終了後に終了遷移スコアを足して終了とします。
なお、今回の例の場合は終了遷移スコアは全て0なので、特段足す必要はありません。
これで遷移スコアを計算する処理は終了となり、最終的にドキュメントごとの各ラベルの合計スコアが算出されました。
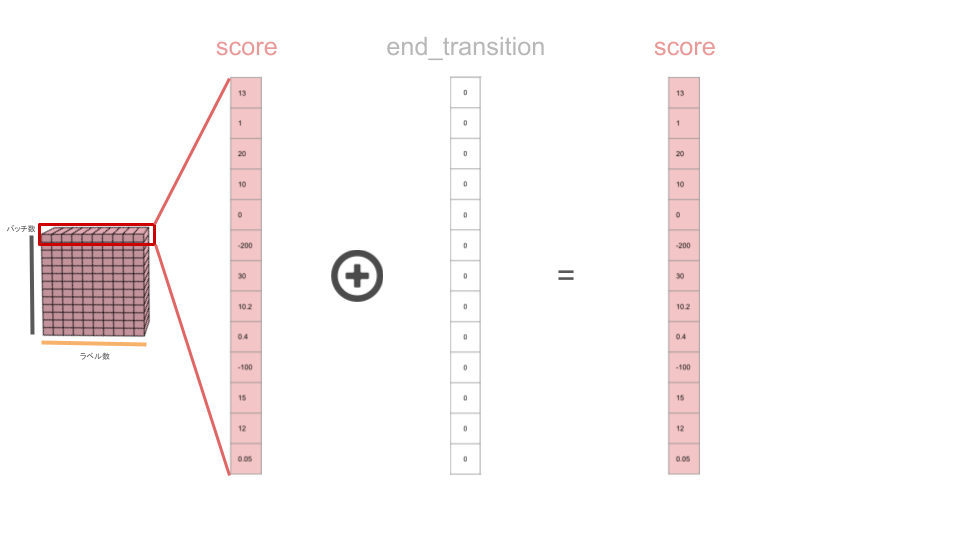
最適なラベル順の再現
ここまでに作成した合計スコアscoreと、直前のラベルとして最もスコア(=可能性)の高いインデックスを格納した履歴historiesを使って、最適なラベルの順番を再現していきます。
ラベルの順番の再現には以下3ステップを実行します。
- 合計スコアのうち最もスコアの高いラベルを特定する
- 最もスコアの高いラベルから順に直前のラベルを配列に格納する
- 最後から順に格納した配列を逆転させて、順方向のラベルの配列を完成させる
いよいよラストスパートです。
順を追って見ていきましょう。
最終スコアのうち最もスコアの高いラベルを特定する
# 各事例で最適なラベル列を取得する
best_labels_list = []
for i in range(batch_size):
# 合計スコアの中で最大のスコアとなるラベルを取得する = 遷移確率を加味した時に最もありうるラベル
_, best_last_label = score[i].max(dim=0)
best_labels = [best_last_label.item()]合計スコアが最も高いスコアをmaxメソッドによって特定し、最も可能性の高いラベルとして格納します。
ここが最適なラベルを求める、遡りの旅のスタート地点になります。
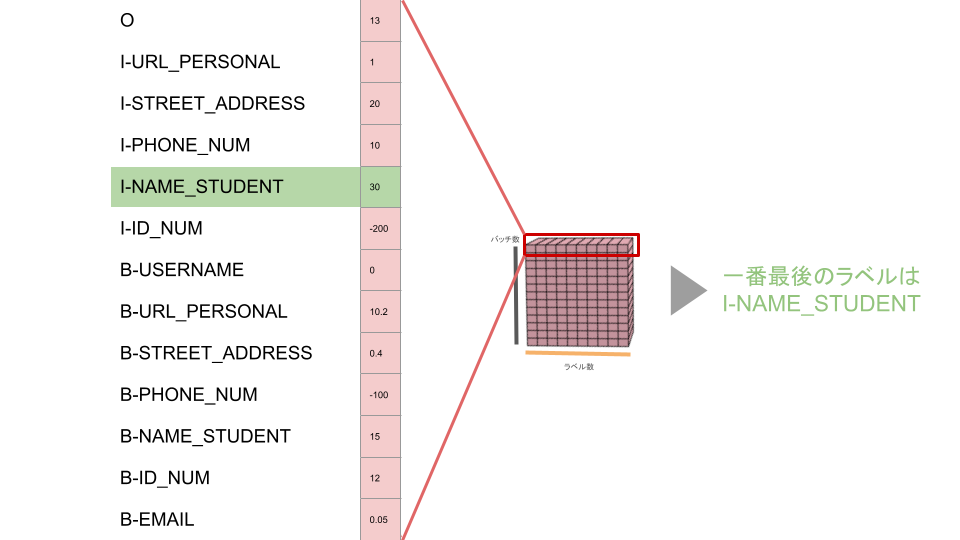
最もスコアの高いラベルから順に直前のラベルを配列に格納する
# ラベルの遷移を逆方向に探索し、最適なラベル列を取得する
for history in reversed(histories): # これで一番最後から辿れる
best_last_label = history[i][best_labels[-1]] # 後ろから逆に直前のラベルIDを取得する
best_labels.append(best_last_label.item())先ほど特定した最適なラベルのスタート地点からどんどんと直前のラベルを特定していきます。
履歴の配列historiesには「あるラベルの直前のラベルはどれである可能性が最も高いか」を示すIDが入っています。
これを順々に遡っていけば文章の全ての最適なラベルを知ることができます。
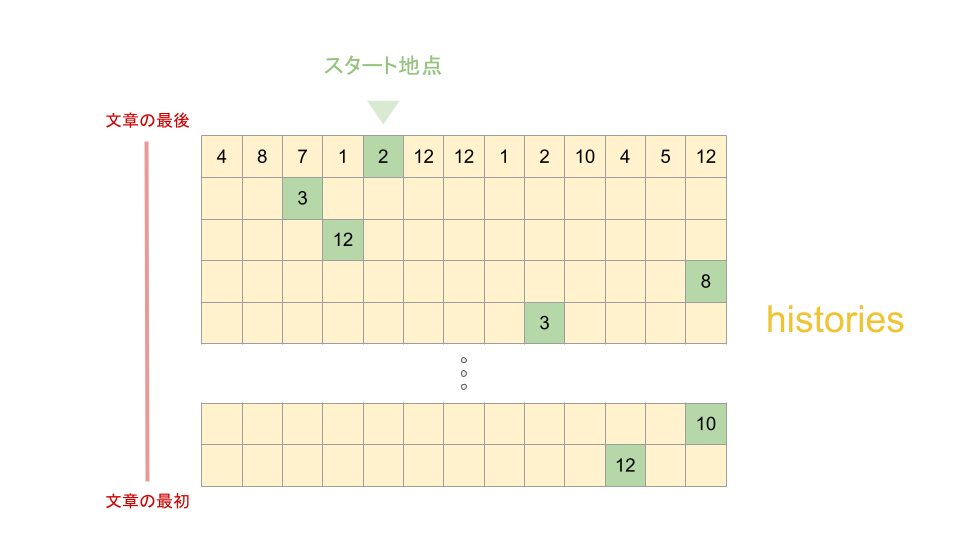
最後から順に格納した配列を逆転させて、順方向のラベルの配列を完成させる
# 順序を反転する
best_labels.reverse()
best_labels_list.append(best_labels)
return torch.LongTensor(best_labels_list)文章の後ろから順に格納したラベルの配列を、逆転させることによって文章の初めから順に格納したラベルの配列を完成させましょう。

まとめ
みなさん、ビタビアルゴリズムの実装の解説を最後までご覧いただき、ありがとうございました!
ところどころ説明が難解なところがあるかと思われますので、コメントにてご指摘をいただければ随時修正させていただきます。
今回の記事における学びは、誰かに説明することを念頭に「どうすればわかりやすく伝わるか」という視点で考えると、難解なアルゴリズムでも少しづつ理解が進んでくる、ということです。
皆さんもぜひ、「ある確率を推定するのに前後の文脈を考慮する必要がある」ような場合にはビタビアルゴリズムを活用して見てください!



コメント