
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題3「M系列による乱数発生プログラムの作成」をPythonで実装していきたいと思います。
M系列による乱数発生法を知らない方にもわかるように解説させていただきますので、ご参考にしていただけると幸いです.
問題文
<M系列による乱数発生プログラムの作成>
適当なプログラム言語を使って、M系列に基づく一様乱数発生のプログラムを作成せよ。
これを使って10,000個の乱数を発生し、これが一様分布からのランダム・サンプルとみなせるかどうかを検定(適合度の検定)せよ。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第11章 P331
M系列とは?
$p > q$とする。
ランダムな1ビットの(1または0からなる)$a_0, a_1, \cdots, a_{p-1}$を用意し、$p$以降の$a_n$については
$$a_n = a_{n-q} + a_{n-p}~~(mod~2)$$
として数列$\{a_n\}$を作成するとき、この数列をM系列という。
M系列に基づく乱数生成法とは?
M系列に基づく乱数生成法では以下3ステップで乱数を生成する。
この時、用意するパラメータは$p, q, l$の3種類
- $a_0$から$a_{p-1}$までランダムな1ビットの数列を用意する
- $a_{p-1}$から$a_{p\times l}$は$a_n=a_{n-p} + a_{n-q}~~(mod~2)$を使って計算し、M系列を用意する。
- $X_0$から$X_{p-1}$までは、M系列の$l$個の要素$a_{i \times l},\cdots,a_{(i +1 ) \times l-1}~(0\geqq l \geqq )$を順に並べて2進整数とする。
- $X_p$以降については$X_n = X_{n-p} \oplus X_{n-q}$で計算をし、欲しいサンプルサイズが生成し終わるまで繰り返す.

排他的論理和の計算
1ビットの排他的論理和については以下のように計算することができます
$$0 \oplus 0 = 0$$
$$1 \oplus 0 = 1$$
$$0 \oplus 1 = 1$$
$$1 \oplus 1 = 0$$
実装コード
M系列に基づく乱数生成法の実装コードは以下の通りです
import math
import numpy as np
import pandas as pd
import random
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
# パラメータの設定
p = 127
q = 63
# 2進数の長さ = 最大数の定義
digits = 2 ** 3
# 生成する乱数のサンプルサイズ
N = 10000
# 一様分布との比較のためのビンのサイズ
bin_ = 0.1
# ランダムなバイナリa_nをa_pまで作成
ans = random.choices([0,1], k = p)
# a_p以降はa_n = a_{n-q} + a_{n-p}で計算
for n in range(p, p * digits):
an = ans[n - p] + ans[n - q]
# 1+1=0で擬似的に排他的論理和を計算
if an == 2:
an = 0
ans.append(an)
# 2進数の文字列同士から排他的論理和を計算する関数
def bitwise_addition_no_carry(bin1, bin2):
# 長さを合わせるためにゼロ埋めする
max_len = max(len(bin1), len(bin2))
bin1 = bin1.zfill(max_len)
bin2 = bin2.zfill(max_len)
# 結果を保存するためのリスト
result = []
# 各ビットごとにXORを計算する
for b1, b2 in zip(bin1, bin2):
sum_bit = int(b1) ^ int(b2) # XORを計算
result.append(str(sum_bit))
# 結果のリストを文字列に変換する
return ''.join(result)
# 2進数を格納する配列
Xns_binary = []
# 10進数を格納する配列
Xns_decimal = []
# [0, 1)の一様乱数を格納する配列
pns = []
for n in range(p):
# a_nからX_nを作成
Xn = ans[n * digits: (n + 1) * digits]
# 配列を文字列に変換
Xn = ''.join(map(str, Xn))
Xns_binary.append(Xn)
# 2進数を10進数に変換
Xn_decimal = int(Xn, 2)
# 10進数を[0, 1)の一様乱数に変換
pn = Xn_decimal / (2**8)
pns.append(pn)
Xns_decimal.append(Xn_decimal)
for n in range(p, N):
# X_n = X_{n-p} + X_{n - q}(排他的論理和)
Xn =bitwise_addition_no_carry(Xns_binary[n - p], Xns_binary[n - q])
Xns_binary.append(Xn)
# 2進数を10進数に計算
Xn_decimal = int(Xn, 2)
# 10進数を[0, 1)の一様乱数に変換
pn = Xn_decimal / (2 ** digits - 1)
pns.append(pn)
Xns_decimal.append(Xn_decimal)
# 適合度検定のため、[0, 1)を等間隔でビニング
range_arr = np.arange(0, 1, bin_)
print(f'range_arr: {range_arr}')
df = pd.DataFrame(columns = ['p', '度数', '期待度数'])
df['p'] = range_arr
for i, f in enumerate(range_arr):
# ビンの幅の中にある乱数の個数をカウント
count = np.sum((f <= pns) & (pns < f + bin_))
df.at[i, '度数'] = count
# 期待度数 = 総数 / ビニング区間の数
df.at[i, '期待度数'] = N / len(range_arr)
df.at[i, 'p'] = f'{str(round(f,3))} ~ {str(round(f + bin_, 3))}'
display(df)
# カイ二乗値を計算する関数
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
# 自由度と有意水準からカイ分布の値を計算
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('生成された乱数は一様分布からのランダムサンプリングとみなせるという仮定は有意水準5%で適合しない')
else:
print('生成された乱数は一様分布からのランダムサンプリングとみなせるという仮定は有意水準5%で適合する')
print()
print()乱数生成コード解説
上記実装は以下5ステップで乱数を生成します
- 1ビットの数列$a_0$から$a_{p-1}$を生成する
- 1ビットの数列$a_p$から$a_{p \times l}$を$a_n = a_{n-p} + a_{n-q}~(mod~2)$に基づいて生成する
- M系列$a_0$から$a_{p \times l}$に基づいて$X_0$から$X_{p-1}$を生成し、10進数に変換する
- $X_p$から$X_{10000}$を$X_n = X_{n-p} \oplus X_{n-q}$に基づいて生成し、2進数→10進数、10進数→[0,1)の一様乱数に変換する
順を追って解説していきます。
1ビットの数列$a_0$から$a_{p-1}$を生成する
import math
import numpy as np
import pandas as pd
import random
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
# パラメータの設定
p = 127
q = 63
# 2進数の長さ = 最大数の定義
digits = 2 ** 3
# 生成する乱数のサンプルサイズ
N = 10000
# 一様分布との比較のためのビンのサイズ
bin_ = 0.1
# ランダムなバイナリa_nをa_pまで作成
ans = random.choices([0,1], k = p)random.choice関数を使って、0または1からランダムに$p$個重複ありで取り出した配列を作成します。
配列の要素$p$個がそれぞれ$a_0$から$a_{p-1}$に対応します。
1ビットの数列$a_p$から$a_{p \times l}$を$a_n = a_{n-p} + a_{n-q}~(mod~2)$に基づいて生成する
# a_p以降はa_n = a_{n-q} + a_{n-p}で計算
for n in range(p, p * digits):
an = ans[n - p] + ans[n - q]
# 1+1=0で擬似的に排他的論理和を計算
if an == 2:
an = 0
ans.append(an)$a_p$から$a_{p \times l}$までは$a_n = a_{n-p} + a_{n-q}~(mod~2)$を計算することによって順次求めていきます。
M系列$a_0$から$a_{p \times l}$に基づいて$X_0$から$X_{p-1}$を生成し、10進数に変換する
# 2進数を格納する配列
Xns_binary = []
# 10進数を格納する配列
Xns_decimal = []
# [0, 1)の一様乱数を格納する配列
pns = []
for n in range(p):
# a_nからX_nを作成
Xn = ans[n * digits: (n + 1) * digits]
# 配列を文字列に変換
Xn = ''.join(map(str, Xn))
Xns_binary.append(Xn)
# 2進数を10進数に変換
Xn_decimal = int(Xn, 2)
# 10進数を[0, 1)の一様乱数に変換
pn = Xn_decimal / (2**8)
pns.append(pn)
Xns_decimal.append(Xn_decimal)ここでは排他的論理和を定義する関数を定義した後で、$X_n$を$a_{n \times l}$から$a_{(n+1) \times l – 1}$までの1と0の配列をくっつけることによって、2進数の整数を作成します。
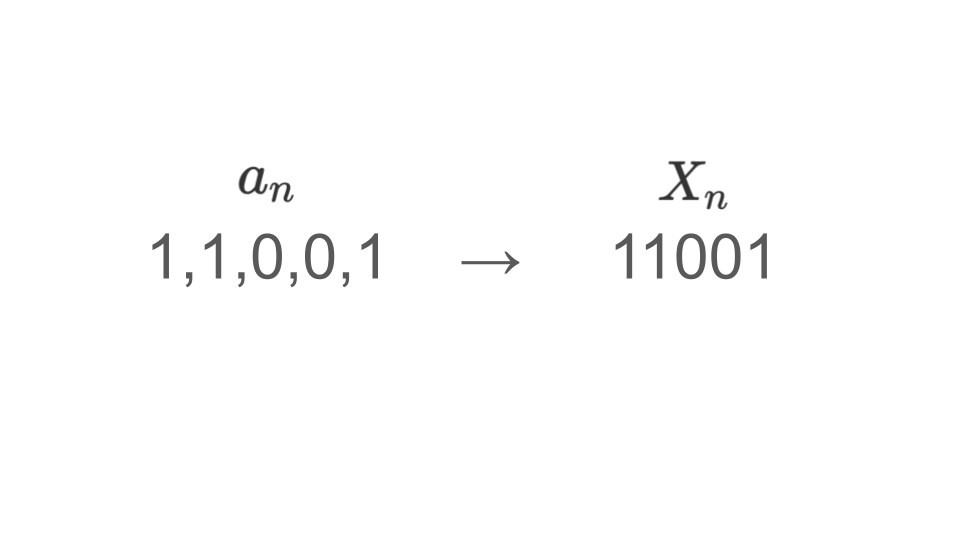
$X_p$から$X_{10000}$を$X_n = X_{n-p} \oplus X_{n-q}$に基づいて生成し、2進数→10進数、10進数→[0,1)の一様乱数に変換する
# 2進数の文字列同士から排他的論理和を計算する関数
def bitwise_addition_no_carry(bin1, bin2):
# 長さを合わせるためにゼロ埋めする
max_len = max(len(bin1), len(bin2))
bin1 = bin1.zfill(max_len)
bin2 = bin2.zfill(max_len)
# 結果を保存するためのリスト
result = []
# 各ビットごとにXORを計算する
for b1, b2 in zip(bin1, bin2):
sum_bit = int(b1) ^ int(b2) # XORを計算
result.append(str(sum_bit))
# 結果のリストを文字列に変換する
return ''.join(result)
....
for n in range(p, N):
# X_n = X_{n-p} + X_{n - q}(排他的論理和)
Xn =bitwise_addition_no_carry(Xns_binary[n - p], Xns_binary[n - q])
Xns_binary.append(Xn)
# 2進数を10進数に計算
Xn_decimal = int(Xn, 2)
# 10進数を[0, 1)の一様乱数に変換
pn = Xn_decimal / (2 ** digits - 1)
pns.append(pn)
Xns_decimal.append(Xn_decimal)最初に排他的論理和を計算する関数を定義し、順次$X_n = X_{n-p} \oplus X_{n-q}$を計算していきます。
最後にint($X_n$, 2)で2進数を10進数に、$\frac{X_n}{2^l – 1}$で10進数を[0,1)の一様乱数に変換します。
なお、$X_n$を$2^l -1$で割り算しているのは、$l$桁の2進数において全ての桁が$1$である時の値を10進数に変換すると$2^l – 1$であるためです。
一様乱数かどうかを確かめる手順
実装においては以下3ステップで、生成した乱数が一様分布からランダムに抽出されたものと言えるかどうかを検定しています。
- 生成した$[0,1)$の範囲の乱数について、0.1の幅ずつ個数をカウントする / 期待度数を算出する
- $\chi^2$値を計算する
- 自由度を求め、有意水準5%の時の$\chi^2$分布と比較する
順を追って解説いたします
生成した$[0,1)$の範囲の乱数について、0.1の幅ずつ個数をカウントする / 期待度数を算出する
# 適合度検定のため、[0, 1)を等間隔でビニング
range_arr = np.arange(0, 1, bin_)
print(f'range_arr: {range_arr}')
df = pd.DataFrame(columns = ['p', '度数', '期待度数'])
df['p'] = range_arr
for i, f in enumerate(range_arr):
# ビンの幅の中にある乱数の個数をカウント
count = np.sum((f <= pns) & (pns < f + bin_))
df.at[i, '度数'] = count
# 期待度数 = 総数 / ビニング区間の数
df.at[i, '期待度数'] = N / len(range_arr)
df.at[i, 'p'] = f'{str(round(f,3))} ~ {str(round(f + bin_, 3))}'適合度検定を行うために、0.1の幅づつビニングを行い、$0〜0.1, 0.1〜0.2, \cdots, 0.9〜1$の区間に含まれる一様乱数の数を数え、データフレームdfの度数列に保存します。
同時にサンプルサイズ$10000$をビニングの区間数10で割った1000を一様乱数を仮定した時の期待度数とします。
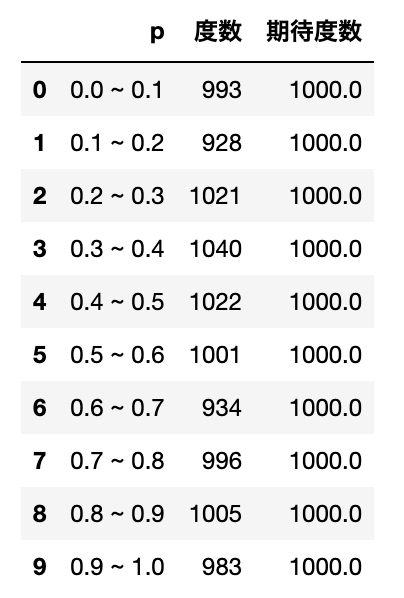
この時点で生成した乱数の度数が期待度数にかなり近しい数字になっていることがわかりますね。
$\chi^2$値を計算する
# カイ二乗値を計算する関数
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
求めた度数と期待度数から$\chi^2$値を計算します。
$\chi^2$値は以下式によって計算することができます。
$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$
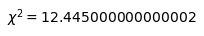
適合度検定について学びたい方へ
適合度検定については「自然科学の統計学」第5章において詳細に解説しており、本ブログでも第5章の演習問題は全て解説しています。
演習問題の解説には適合度検定をPythonで実装する方法や適合度検定の式などについても詳細に解説しておりますので、適合度検定について詳しく勉強したい方は第5章の演習問題の解説をご覧ください
自由度を求め、有意水準5%の時の$\chi^2$分布と比較する
# 自由度 (度数の数 - 1)
v = len(df) - 1
print(f'自由度: {v}')
alpha = 0.05
# 自由度と有意水準からカイ分布の値を計算
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('生成された乱数は一様分布からのランダムサンプリングとみなせるという仮定は有意水準5%で適合しない')
else:
print('生成された乱数は一様分布からのランダムサンプリングとみなせるという仮定は有意水準5%で適合する')
print()
print()自由度は度数の数$-1$で計算することができるので、
$$\ = 10 – 1$$
と求めることができます。
そして、自由度$9$の有意水準5%における$\chi^2$分布の値はchi2.ppf関数を使用すると
$$\chi^2_{0.05}(9) = 16.918$$
と求めることができ、先ほど求めた$\chi^2$値と比較すると
$$\chi^2 = 12.445 < \chi^2_{0.05}(9) = 16.918$$
であり、生成した乱数が一様乱数であるという仮定を棄却できないことがわかります.
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第11章-演習問題3「M系列による乱数発生プログラムの作成」をPythonで実装して、コードが解答を導く手順を詳細に解説していきました。
今回の実装を参考に指定いただければ、一様分布に基づいて乱数を生成することはもちろん、その乱数が一様分布からランダム抽出してものと言えるということも担保できるかと思われます。(random.uniformを使えばいいじゃんと言われればそれまでですが…)
皆さんの中でも乱数生成に興味が湧いた方は、ぜひ本記事の乱数生成方法を参考に乱数を生成していただけると幸いです!




コメント