
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題5「ベイズ診断」についてPythonで解いていきたいと思います。
今回の問題はある病気に対する症状の確率(尤度=もっともらしさ)が得られているときに、病気である確率と病気でない確率のどちらの方が高いのかをベイズの観点から推定する問題となっており、ベイズ統計学を理解する上で重要な問題となっています。
今回の問題を通して、ベイズ統計学に対する理解を深めていただけると幸いです。
問題文
<ベイズ診断>
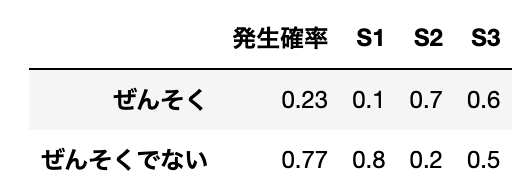
ある疾病$D$(例えば、ぜんそく)があるかどうかを診断するために、3つの症候$S_1, S_2, S_3$があるかどうかを調べるものとする。
$S_1, S_2, S_3$はそれぞれ確率的に生じ、かつ独立とし、また、$D$の場合と$D$でない場合$\bar{D}$(正常な時)とでは、これらの症候の確率(尤度)が異なり、以下の表で与えられている。
なお、疾病$D$の発生確率(統計的な発生率)も事前に与えられている。
i ) 症候$S_3$はなく、$S_1, S_2$がある時、このパターンを$S = (1, 0, 0)$と表す。この時の、$D$の事後確率$P(D|S)$、$\bar{D}$の事後確率$P(\bar{D}|S)$を求めよ
ii ) 比$\Omega(S) = \frac{P(D|S)}{P(\bar{D}|S)}$を、8通りのすべてのパターン$S$について計算し、大きさの順に並べよ。
また、この比を最大にする(最も高い可能性で’ぜんそく’と診断される)症候のパターンはどれか。
iii ) 事後オッズ$\Omega(S)$の大きさの順序は、尤度比$\lambda(S) = \frac{P(S|D)}{P(S|\bar{D})}$の順序に一致することを示せ。
また、$\lambda(S) \geqq 1$となるパターン$S$をすべて挙げよ。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第9章 演習問題 P273~274
事後確率の計算方法
母数$\theta$が離散的である時、$z$を標本のデータ、尤度関数を$f(z|\theta_i)$、事前確率を$w(\theta_i)$とすると、事後確率$w'(\theta_i | z)$は次のような式で得られる。
$$w'(\theta_i | z) = \frac{w(\theta_i) \cdot f(z|\theta_i)}{\sum w(\theta_i) \cdot f(z|\theta_i)}$$
実装コード
本問題を解くためのコードは以下のように実装できる。
import numpy as np
import pandas as pd
import itertools
# (i)
# S=(1,1,0)の時のP(D)P(S | D)
pdsd = 0.23 * 0.1 * 0.7 * 0.4
# S=(1,1,0)の時のP(bar(D))P(S | bar(D))
pbdsd = 0.77 * 0.8 * 0.2 * 0.5
# S = (1,1,0)の時のP(D|S)
pds = pdsd / (pdsd + pbdsd)
print(f'Dの事後確率: {pds}')
# S= (1,1,0)の時のP(bar(D) | S)
pbds = pbdsd / (pdsd + pbdsd)
print(f'bar(D)の事後確率: {pbds}')
print()
# (ii)/(iii)
# P(D)
priord = 0.23
# P(bar(D))
priord_bar = 0.77
# D(ぜんそく)というデータが得られた時の尤度関数
likelihoodd = np.array([0.1, 0.7, 0.6])
# D(ぜんそく)というデータが得られた時の1 - 尤度関数
inv_likelihoodd = 1- likelihoodd
# bar(D)(ぜんそくでない)というデータが得られた時の尤度関数
likelihoodd_bar = np.array([0.8, 0.2, 0.5])
# bar(D)(ぜんそくでない)というデータが得られた時の1 - 尤度関数
inv_likelihoodd_bar = [1,1,1] - likelihoodd_bar
# すべてのSのペアを計算
ss = [0,1]
ss = list(itertools.product(ss,ss,ss))
# Omegaが最大である時のSを保存するための準備
max_omegas = 0
max_s = []
# SをOmegaが大きい順に並べるための配列の準備
omegass = []
lambdass = []
# Sを取り出して処理を開始
for s in ss:
# (ii)
# P(D|S)の初期化
pdsd = priord
# P(bar(D) | S)の初期化
pbdsd = priord_bar
# (iii)
# P(S | D)の初期化
psd = 1
# P(S | bar(D))の初期化
psbd = 1
# iは尤度関数の取り出しに使用、symptomは尤度関数と1-尤度関数のどちらを使用するかを判断するために使用
for i, symptom in enumerate(s):
# P(S_i | D)を求める
sd = likelihoodd[i] if symptom == 1 else inv_likelihoodd[i]
# (ii)
pdsd *= sd
# (iii)
psd *= sd
# P(S_i | bar(D))を求める
sdb = likelihoodd_bar[i] if symptom == 1 else inv_likelihoodd_bar[i]
# (ii)
pbdsd *= sdb
# (iii)
psbd *= sdb
# P(D|S), P(bar(D) | S)の分母の計算
sum_ = pdsd + pbdsd
# P(D | S)
pds = pdsd / sum_
# P(bar(D) | S)
pbds = pbdsd / sum_
# Omega(S)の導出
omegas = pdsd / pbdsd
# lambda(S)の導出
lambdas = psd /psbd
# 順番に並べるために配列に格納
omegass.append(omegas)
lambdass.append(lambdas)
print(f'S = {s}の場合: P(D | S) = {pds}, P(bar(D) | S) = {pbds}, OMEGA(S) = {omegas}')
# 最大のOmega(S)の更新
if omegas > max_omegas:
max_omegas = omegas
max_s = s
print(f'S ={max_s}の時に事後オッズ{max_omegas}でぜんそくと診断される')
df = pd.DataFrame()
df['S'] = ss
df['Omega'] = omegass
# Omega(S)順に並び替え
df = df.sort_values('Omega', ascending= False)
display(df)
df = pd.DataFrame()
df['S'] = ss
df['Lambda'] = lambdass
df = df.sort_values('Lambda', ascending= False)
display(df)
# lambda(S) >= 1であるようなSを抽出
df_s_up_1 = df.query('Lambda >= 1')
ss = df_s_up_1['S'].to_list()
print(f'lambda(s) >= 1となるのは、以下の{len(ss)}通り: {ss}')(i)の解説
# (i)
# S=(1,1,0)の時のP(D)P(S | D)
pdsd = 0.23 * 0.1 * 0.7 * 0.4
# S=(1,1,0)の時のP(bar(D))P(S | bar(D))
pbdsd = 0.77 * 0.8 * 0.2 * 0.5
# S = (1,1,0)の時のP(D|S)
pds = pdsd / (pdsd + pbdsd)
print(f'Dの事後確率: {pds}')
# S= (1,1,0)の時のP(bar(D) | S)
pbds = pbdsd / (pdsd + pbdsd)
print(f'bar(D)の事後確率: {pbds}')(i)は以下の3ステップで解いています。
- $S = (1,1,0)の時の$$P(D)P(S|D)$の計算
- $S = (1,1,0)の時の$$P(\bar{D})P(S|\bar{D})$の計算
- $P(D|S), P(\bar{D} | S)$の計算
順を追って解説していきます。
$S = (1,1,0)の時の$P(D)P(S|D)$の計算
# S=(1,1,0)の時のP(D)P(S | D)
pdsd = 0.23 * 0.1 * 0.7 * 0.4状態$D$(ぜんそく)である時の各症候がある確率$S_1, S_2, S_3$はそれぞれ$0.1, 0.7, 0.6$である。
一方、状態$D$(ぜんそく)である時の各症候がない確率$\bar{S_1}, \bar{S_2}, \bar{S_3}$はそれぞれ$0.9, 0.3, 0.4$である。
また、状態$D$になる確率$P(D)$が$0.23$であるから、症候$S_3$がないことに注意をすると$P(D)P(S|D)$の計算は以下のようになる
$$P(D)P(S|D) = 0.23 \times 0.1 \times 0.7 \times (1 – 0.6) =0.23 \times 0.1 \times 0.7 \times 0.4$$
$S = (1,1,0)の時の$P(\bar{D})P(S|\bar{D})$の計算
# S=(1,1,0)の時のP(bar(D))P(S | bar(D))
pbdsd = 0.77 * 0.8 * 0.2 * 0.5状態$\bar{D}$(ぜんそくでない)である時の各症候がある確率$S_1, S_2, S_3$はそれぞれ$0.8, 0.2, 0.5$である。
一方、状態$\bar{D}$(ぜんそくでない)である時の各症候がない確率$\bar{S_1}, \bar{S_2}, \bar{S_3}$はそれぞれ$0.2, 0.8, 0.5$である。
また、状態$\bar{D}$になる確率$P(\bar{D})$が$0.77$であるから、症候$S_3$がないことに注意をすると$P(\bar{D})P(S|\bar{D})$の計算は以下のようになる
$$P(\bar{D})P(S|\bar{D}) = 0.77 \times 0.8 \times 0.2 \times (1 – 0.5) =0.77 \times 0.8 \times 0.2 \times 0.5$$
$P(D|S), P(\bar{D} | S)$の計算
# S = (1,1,0)の時のP(D|S)
pds = pdsd / (pdsd + pbdsd)
print(f'Dの事後確率: {pds}')
# S= (1,1,0)の時のP(bar(D) | S)
pbds = pbdsd / (pdsd + pbdsd)
print(f'bar(D)の事後確率: {pbds}')$P(D|S), P(\bar{D] | S)$はそれぞれ以下の式で計算される。
$$P(D|S) = \frac{P(D)P(S|D)}{P(D)P(S|D) + P(\bar{D})P(S|\bar{D})}$$
$$P(\bar{D}|S) = \frac{P(\bar{D})P(S|\bar{D})}{P(D)P(S|D) + P(\bar{D})P(S|\bar{D})}$$

(ii)/(iii)の解説
# (ii)/(iii)
# P(D)
priord = 0.23
# P(bar(D))
priord_bar = 0.77
# D(ぜんそく)というデータが得られた時の尤度関数
likelihoodd = np.array([0.1, 0.7, 0.6])
# D(ぜんそく)というデータが得られた時の1 - 尤度関数
inv_likelihoodd = 1- likelihoodd
# bar(D)(ぜんそくでない)というデータが得られた時の尤度関数
likelihoodd_bar = np.array([0.8, 0.2, 0.5])
# bar(D)(ぜんそくでない)というデータが得られた時の1 - 尤度関数
inv_likelihoodd_bar = [1,1,1] - likelihoodd_bar
# すべてのSのペアを計算
ss = [0,1]
ss = list(itertools.product(ss,ss,ss))
# Omegaが最大である時のSを保存するための準備
max_omegas = 0
max_s = []
# SをOmegaが大きい順に並べるための配列の準備
omegass = []
lambdass = []
# Sを取り出して処理を開始
for s in ss:
# (ii)
# P(D)P(S|D)の初期化
pdsd = priord
# P(bar(D))P(S|bar(D))の初期化
pbdsd = priord_bar
# (iii)
# P(S | D)の初期化
psd = 1
# P(S | bar(D))の初期化
psbd = 1
# iは尤度関数の取り出しに使用、symptomは尤度関数と1-尤度関数のどちらを使用するかを判断するために使用
for i, symptom in enumerate(s):
# P(S_i | D)を求める
sd = likelihoodd[i] if symptom == 1 else inv_likelihoodd[i]
# (ii)
pdsd *= sd
# (iii)
psd *= sd
# P(S_i | bar(D))を求める
sdb = likelihoodd_bar[i] if symptom == 1 else inv_likelihoodd_bar[i]
# (ii)
pbdsd *= sdb
# (iii)
psbd *= sdb
# P(D|S), P(bar(D) | S)の分母の計算
sum_ = pdsd + pbdsd
# P(D | S)
pds = pdsd / sum_
# P(bar(D) | S)
pbds = pbdsd / sum_
# Omega(S)の導出
omegas = pdsd / pbdsd
# lambda(S)の導出
lambdas = psd /psbd
# 順番に並べるために配列に格納
omegass.append(omegas)
lambdass.append(lambdas)
print(f'S = {s}の場合: P(D | S) = {pds}, P(bar(D) | S) = {pbds}, OMEGA(S) = {omegas}')
# 最大のOmega(S)の更新
if omegas > max_omegas:
max_omegas = omegas
max_s = s
print(f'S ={max_s}の時に事後オッズ{max_omegas}でぜんそくと診断される')
df = pd.DataFrame()
df['S'] = ss
df['Omega'] = omegass
# Omega(S)順に並び替え
df = df.sort_values('Omega', ascending= False)
display(df)
df = pd.DataFrame()
df['S'] = ss
df['Lambda'] = lambdass
df = df.sort_values('Lambda', ascending= False)
display(df)
# lambda(S) >= 1であるようなSを抽出
df_s_up_1 = df.query('Lambda >= 1')
ss = df_s_up_1['S'].to_list()
print(f'lambda(s) >= 1となるのは、以下の{len(ss)}通り: {ss}')(ii)と(iii)は求める値が$\Omega(S)$, $\lambda(S)$で異なるものの、大まかな計算過程は同じなので、同一の処理の中に盛り込みました。
(ii)と(iii)を解くためのコードとしては、以下7つの手順で処理を進めています。
- 事前確率、尤度、$S$のペアを用意する
- すべてのSに対して$P(D)P(S|D)$と$P(\bar{D})P(S|\bar{D})$を求める
- $P(D|S)$と$P(\bar{D}|S)$を求める
- $\Omega(S)$と$\lambda(S)$を求める
- (ii) $\Omega(S)$が最大になるときのSを求める
- (ii) $\Omega(S)$が大きい順になるようにデータフレームを作成する
- (iii) $\lambda(S) \geqq 1$となるようなパターン$S$を求める
順を追って解説していきます。
事前確率、尤度、$S$のペアを用意する
# (ii)/(iii)
# P(D)
priord = 0.23
# P(bar(D))
priord_bar = 0.77
# D(ぜんそく)というデータが得られた時の尤度関数
likelihoodd = np.array([0.1, 0.7, 0.6])
# D(ぜんそく)というデータが得られた時の1 - 尤度関数
inv_likelihoodd = 1- likelihoodd
# bar(D)(ぜんそくでない)というデータが得られた時の尤度関数
likelihoodd_bar = np.array([0.8, 0.2, 0.5])
# bar(D)(ぜんそくでない)というデータが得られた時の1 - 尤度関数
inv_likelihoodd_bar = [1,1,1] - likelihoodd_bar
# すべてのSのペアを計算
ss = [0,1]
ss = list(itertools.product(ss,ss,ss))
# Omegaが最大である時のSを保存するための準備
max_omegas = 0
max_s = []
# SをOmegaが大きい順に並べるための配列の準備
omegass = []
lambdass = []次の手順以降ではfor文を使って処理を作成していくため、for文で処理をしやすいように変数や配列を準備しておきます。
すべてのSに対して$P(D)P(S|D)$と$P(\bar{D})P(S|\bar{D})$を求める
# Sを取り出して処理を開始
for s in ss:
# (ii)
# P(D)P(S|D)の初期化
pdsd = priord
# P(bar(D))P(S|bar(D))の初期化
pbdsd = priord_bar
# (iii)
# P(S | D)の初期化
psd = 1
# P(S | bar(D))の初期化
psbd = 1
# iは尤度関数の取り出しに使用、symptomは尤度関数と1-尤度関数のどちらを使用するかを判断するために使用
for i, symptom in enumerate(s):
# P(S_i | D)を求める
sd = likelihoodd[i] if symptom == 1 else inv_likelihoodd[i]
# (ii)
pdsd *= sd
# (iii)
psd *= sd
# P(S_i | bar(D))を求める
sdb = likelihoodd_bar[i] if symptom == 1 else inv_likelihoodd_bar[i]
# (ii)
pbdsd *= sdb
# (iii)
psbd *= sdbfor文を使って、すべてのパターン$S$について$P(D)P(S|D)$と$P(\bar{D})P(S|\bar{D})$を求めていきます。
この時、$S$の配列の中の値が1であるか0であるかによって、かけ算する尤度を使い分けている点に注意しましょう。
$P(D|S)$と$P(\bar{D}|S)$を求める
# P(D|S), P(bar(D) | S)の分母の計算
sum_ = pdsd + pbdsd
# P(D | S)
pds = pdsd / sum_
# P(bar(D) | S)
pbds = pbdsd / sum_以下の式に則り、$P(D|S)$と$P(\bar{D}|S)$を計算します。
$$P(D|S) = \frac{P(D)P(S|D)}{P(D)P(S|D) + P(\bar{D})P(S|\bar{D})}$$
$$P(\bar{D}|S) = \frac{P(\bar{D})P(S|\bar{D})}{P(D)P(S|D) + P(\bar{D})P(S|\bar{D})}$$
$\Omega(S)$と$\lambda(S)$を求める
# Omega(S)の導出
omegas = pdsd / pbdsd
# lambda(S)の導出
lambdas = psd /psbd
# 順番に並べるために配列に格納
omegass.append(omegas)
lambdass.append(lambdas)
print(f'S = {s}の場合: P(D | S) = {pds}, P(bar(D) | S) = {pbds}, OMEGA(S) = {omegas}')
以下の式に則り、$\Omega(S)$と$\lambda(S)$を計算します。
$$\Omega(S) = \frac{P(D|S)}{P(\bar{D}|S)}$$
$$\lambda(S) = \frac{P(S|D)}{P(S|\bar{D})}$$
ここで、(iii)の「事後オッズ$\Omega(S)$の大きさの順序は、尤度比$\lambda(S) = \frac{P(S|D)}{P(S|\bar{D})}$の順序に一致することを示せ。」を証明しておきましょう。
$P(D|S)$と$P(\bar{D]|S)$の分母$P(D)P(S|D) + P(\bar{D})P(S|\bar{D})$は同一であるため、$\Omega(S)$は以下のように式変形することができます。
$$\Omega(S) = \frac{P(D)P(S|D)}{P(\bar{D})P(S|\bar{D})} = \frac{P(D)}{P(\bar{D})}\cdot\frac{P(S|D)}{P(S|\bar{D})} = \frac{P(D)}{P(\bar{D})}\cdot \lambda(S)$$
ここで、$P(D)P(S|D) + P(\bar{D})P(S|\bar{D}) = \frac{0.23}{0.77} = 0.299$となり、$\Omega(S)$は$\lambda(S)$の0.299倍であることから、事後オッズ$\Omega(S)$と尤度比$\lambda(S)$の順序が一致するのは至極当然と言えます。
(ii) $\Omega(S)$が最大になるときのSを求める
# 最大のOmega(S)の更新
if omegas > max_omegas:
max_omegas = omegas
max_s = s
print(f'S ={max_s}の時に事後オッズ{max_omegas}でぜんそくと診断される')変数max_omegasを毎回のomegasの値と比較して更新、更新が行われた時の$S$の値も更新することによって、事後オッズ$\Omega(S)$が最大になる時の$S$を求めることができます。
(ii) $\Omega(S)$が大きい順になるようにデータフレームを作成する
df = pd.DataFrame()
df['S'] = ss
df['Omega'] = omegass
# Omega(S)順に並び替え
df = df.sort_values('Omega', ascending= False)
display(df)df.sort_values()により、$\Omega(S)$が大きい順に配列を並び替えています。

(iii) $\lambda(S) \geqq 1$となるようなパターン$S$を求める
df = pd.DataFrame()
df['S'] = ss
df['Lambda'] = lambdass
df = df.sort_values('Lambda', ascending= False)
display(df)
# lambda(S) >= 1であるようなSを抽出
df_s_up_1 = df.query('Lambda >= 1')
ss = df_s_up_1['S'].to_list()
print(f'lambda(s) >= 1となるのは、以下の{len(ss)}通り: {ss}')df.query()の条件に「Lambda列の値が1以上であること」という条件を付与することによって、$\lambda(S)\geqq 1$となるような$S$のペアを抽出しています。
ついでに、$\lambda(S)$を大きい順に並べることによって、$\Omega(S)$の並び順と同一であることも示しています。

まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第9章-演習問題5「ベイズ診断」についてPythonで解き、解説をいたしました。
変数が多くなってしまいましたが、やっていること自体は非常にシンプルであることがご理解いただけたかと思います。
今回の問題のように、事象の発生確率と、事象と相関のある尤度が分かれば、事後確率を求めることができますので、ぜひご活用いただければと思います!



コメント