
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題7「正規性の仮定のチェック」をPythonで解いていきたいと思います。
今回の問題では正規確率紙をmatplotlibで実装したり、標本r次モーメントの関数が出てきたりと、自身でも知らなかったトピックが複数できてたので、皆さんにも何かしらの学びがあると幸いです!
問題文
<正規性の仮定のチェック>
次のデータ(A),(B)について、それぞれ
i ) 正規確率紙へのプロットを行い、考察せよ
ii ) 標本歪度$b_1$及ぼ標本尖度$b_2$を求めよ。データは正規分布からのものとみなせるか
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第7章 演習問題 P229
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
標本$r$次モーメント、標本歪度、標本尖度とは?
母集団の$r$次モーメントが
$$\mu’_{r} = \int_\infty^\infty (x-\mu)^r f(x) dx$$
と表されるのに対し、
$$m’_r = \sum (X_i – \bar{X})^2 /n$$
で表される値を標本r次モーメントと呼びます。
そして、この標本r次モーメントを利用すると、以下の式のようにして標本歪度$b_1$と標本尖度$b_2$を求めることができます。
$$b_1 = \frac{m’_3}{(m’_2)^{3/2}}$$
$$b_2 = \frac{m’_4}{(m’_2)^2} – 3$$
標本歪度は3乗によって標本に偏りがある場合はそれをより強調するような尺度に、標本尖度は4乗によって標本が平均より遠い値が大きく重み付けされるため、より裾の長さを強調するような尺度となっています。
正規分布では標本歪度と標本尖度は計算上0となるため、標本数に応じたある一定の値よりお大きい場合は正規性の仮定を棄却することができます。
本書に掲載の表では、標本数$n=15$の場合、標本歪度では0.9以上、標本尖度では1.1以上の場合に正規性の仮定が棄却されるとされています。
正規確率紙とは?
ある正規分布$N(\mu, \sigma^2)$について、$Z = (X_i – \mu)/ \sigma$は標準正規分布に従うことから、$X_i$が特定の$x$以下になる確率$p_x$は累積分布関数$\Phi(z)$を用いて、
$$p_x = \Phi(\frac{x – \mu}\sigma)$$
と表され、$\Phi$の逆関数を$\Phi^{-1}$とすると
$$\Phi(p_x)^{-1} = \frac{x – \mu}\sigma$$
と同等である。
上の2つ目の式から、ある標本$X_i, \cdots,X_n$が正規性を満たす場合は、その点を小さいものから順番にプロットすると1次直線になることが$\Phi(p_x)^{-1} = \frac{x – \mu}\sigma$という式から考察できる。
そのため、正規確率紙という対数方眼紙のような紙に、$X_i, \cdots, X_n$を小さい順に並びかえ、
$$(X_i,~z_i)~~~~z_i = \Phi\left(\frac{i}{n + 1}\right),~~i = 1,2,\cdots,n$$
をプロットすると、正規性を満たす場合はほぼ直線のようなグラフになる。
実装コード
本問題を解くためのPythonコードは以下の通りです
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm
df = pd.read_csv('Checking_Assumptions_of_Normality.csv')
display(df)
arr1 = df.A
arr2 = df.B
arr1 = sorted(arr1)
arr2 = sorted(arr2)
n = len(arr1)
zi1 = [ norm.ppf(i/(n + 1), loc = 0, scale = 1) for i in range(1, n + 1)]
#==============================
# グラフ1
#==============================
fig = plt.figure(figsize=(7,8))
xmin= 10
xmax= 14
ymin=norm.ppf(0.0001, loc=0, scale=1)
ymax=norm.ppf(0.9999, loc=0, scale=1)
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.tick_params(labelbottom='off')
plt.tick_params(labelleft='off')
plt.tick_params(labelleft=False)
plt.tick_params(which='both', width=0)
# setting of x-y axes
_dy=np.array([0.01,0.1,0.5,0.9,0.99])
dy=norm.ppf(_dy, loc=0, scale=1)
print(dy)
plt.hlines(dy, xmin, xmax, color='grey')
_dx=np.arange(10,14,0.1)
dx=_dx
plt.vlines(dx, ymin, ymax, color='grey')
fs=16
for i in range(0,5):
plt.text(xmin-0.01, dy[i], str(_dy[i] * 100), ha = 'right', va = 'center', fontsize=fs)
plt.text(0.5*(xmin+xmax), ymin-0.5, 'Flood discharge (m$^3$/s)', ha = 'center', va = 'center', fontsize=fs)
plt.text(xmin-0.5,0.5*(ymin+ymax),'Non-exceedance probability', ha = 'center', va = 'center', fontsize=fs, rotation=90)
plt.scatter(arr1, zi1)
# image saving and image showing
plt.savefig('fig_flood_p.png', bbox_inches="tight", pad_inches=0.2)
plt.show()
#==============================
# グラフ2
#==============================
fig = plt.figure(figsize=(7,8))
xmin= 6
xmax= 38
ymin=norm.ppf(0.0001, loc=0, scale=1)
ymax=norm.ppf(0.9999, loc=0, scale=1)
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.tick_params(labelbottom='off')
plt.tick_params(labelleft='off')
plt.tick_params(labelleft=False)
plt.tick_params(which='both', width=0)
# setting of x-y axes
_dy=np.array([0.01,0.1,0.5,0.9,0.99])
dy=norm.ppf(_dy, loc=0, scale=1)
print(dy)
plt.hlines(dy, xmin, xmax, color='grey')
_dx=np.arange(6,38,0.5)
dx=_dx
plt.vlines(dx, ymin, ymax, color='grey')
fs=16
for i in range(0,5):
plt.text(xmin-0.01, dy[i], str(_dy[i] * 100), ha = 'right', va = 'center', fontsize=fs)
plt.text(0.5*(xmin+xmax), ymin-0.5, 'Flood discharge (m$^3$/s)', ha = 'center', va = 'center', fontsize=fs)
plt.text(xmin-5,0.5*(ymin+ymax),'Non-exceedance probability', ha = 'center', va = 'center', fontsize=fs, rotation=90)
plt.scatter(arr2, zi1)
# image saving and image showing
plt.savefig('fig_flood_p.png', bbox_inches="tight", pad_inches=0.2)
plt.show()
##########
# (ii)
##########
arrs = [arr1, arr2]
def mr(arr, r, n):
mr = np.sum((arr - np.mean(arr))** r) / n
return mr
for i, arr in enumerate(arrs):
m2 = mr(arr, 2, n)
m3 = mr(arr, 3, n)
m4 = mr(arr, 4, n)
b1 = m3 / (m2 ** (3/2))
b2 = m4 / (m2 ** 2) - 3
print(f'標本{i + 1}の標本歪度: {b1}')
print(f'標本{i + 1}の標本尖度: {b2}')
if b1 > 0.9 or b2 > 1.1:
print('有意水準5%で母分布が正規分布という仮定は棄却される')
else:
print('有意水準5%で母分布が正規分布という仮定は棄却されない')(i)の解説
(i)は以下の2ステップで解くことができます。
- norm.ppfを利用して累積分布関数の逆関数を適用した配列を求める
- 正規確率紙をmatplotlibで再現し、点$(X_i, z_i)$を描画する
順を追って解説していきます。
norm.ppfを利用して累積分布関数の逆関数を適用した配列を求める
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm
df = pd.read_csv('Checking_Assumptions_of_Normality.csv')
display(df)
arr1 = df.A
arr2 = df.B
arr1 = sorted(arr1)
arr2 = sorted(arr2)
n = len(arr1)
zi1 = [ norm.ppf(i/(n + 1), loc = 0, scale = 1) for i in range(1, n + 1)]累積分布関数の逆関数はPythonではscipy.stats.norm.ppfでパーセントポイント関数として定義されています。
このパーセントポイント関数は引数として確率XX%を与えると、累積分布関数がXX%であるような時の確率変数を教えてくれます。
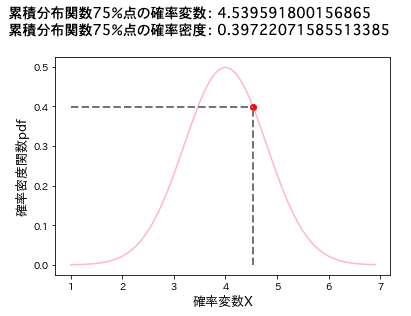
このppf関数によって、$z_i = \Phi^{-1}\left(\frac{i}{n + 1}\right)$の配列を作成します.
正規確率紙をmatplotlibで再現し、点$(X_i, z_i)$を描画する
#==============================
# グラフ1
#==============================
fig = plt.figure(figsize=(7,8))
xmin= 10
xmax= 14
ymin=norm.ppf(0.0001, loc=0, scale=1)
ymax=norm.ppf(0.9999, loc=0, scale=1)
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.tick_params(labelbottom='off')
plt.tick_params(labelleft='off')
plt.tick_params(labelleft=False)
plt.tick_params(which='both', width=0)
# setting of x-y axes
_dy=np.array([0.01,0.1,0.5,0.9,0.99])
dy=norm.ppf(_dy, loc=0, scale=1)
print(dy)
plt.hlines(dy, xmin, xmax, color='grey')
_dx=np.arange(10,14,0.1)
dx=_dx
plt.vlines(dx, ymin, ymax, color='grey')
fs=16
for i in range(0,5):
plt.text(xmin-0.01, dy[i], str(_dy[i] * 100), ha = 'right', va = 'center', fontsize=fs)
plt.text(0.5*(xmin+xmax), ymin-0.5, 'Flood discharge (m$^3$/s)', ha = 'center', va = 'center', fontsize=fs)
plt.text(xmin-0.5,0.5*(ymin+ymax),'Non-exceedance probability', ha = 'center', va = 'center', fontsize=fs, rotation=90)
plt.scatter(arr1, zi1)
# image saving and image showing
plt.savefig('fig_flood_p.png', bbox_inches="tight", pad_inches=0.2)
plt.show()
#==============================
# グラフ2
#==============================
fig = plt.figure(figsize=(7,8))
xmin= 6
xmax= 38
ymin=norm.ppf(0.0001, loc=0, scale=1)
ymax=norm.ppf(0.9999, loc=0, scale=1)
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.tick_params(labelbottom='off')
plt.tick_params(labelleft='off')
plt.tick_params(labelleft=False)
plt.tick_params(which='both', width=0)
# setting of x-y axes
_dy=np.array([0.01,0.1,0.5,0.9,0.99])
dy=norm.ppf(_dy, loc=0, scale=1)
print(dy)
plt.hlines(dy, xmin, xmax, color='grey')
_dx=np.arange(6,38,0.5)
dx=_dx
plt.vlines(dx, ymin, ymax, color='grey')
fs=16
for i in range(0,5):
plt.text(xmin-0.01, dy[i], str(_dy[i] * 100), ha = 'right', va = 'center', fontsize=fs)
plt.text(0.5*(xmin+xmax), ymin-0.5, 'Flood discharge (m$^3$/s)', ha = 'center', va = 'center', fontsize=fs)
plt.text(xmin-5,0.5*(ymin+ymax),'Non-exceedance probability', ha = 'center', va = 'center', fontsize=fs, rotation=90)
plt.scatter(arr2, zi1)
# image saving and image showing
plt.savefig('fig_flood_p.png', bbox_inches="tight", pad_inches=0.2)
plt.show()上記コードによって、正規確率紙を再現し、それぞれデータを格納した配列arr1,arr2と先ほど計算した$z_i$を利用して正規性を検証するためのグラフを出力しています。
配列arr1とarr2はデータ範囲が異なるので、xminとxmaxでグラフの描画範囲を調整しています。
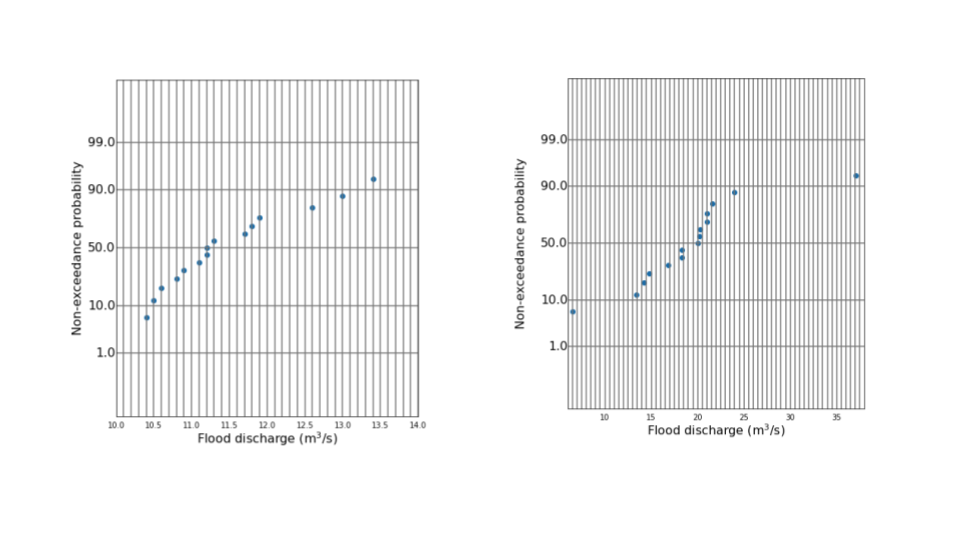
上記図を見てみると、データAの方はある程度直線的な関係が見えるのに対し、データBの方はデータの両端の値が離れており、裾の広さが正規確率紙への描画から見て取れます。
(ii)の解説
(ii)の問題は以下の3ステップによって解くことができます。
- 標本$r$次モーメントを計算する関数mrを定義する
- 関数mrを利用し、標本歪度$b_1$と標本尖度$b_2$をデータA、データBについてそれぞれ計算する
- 標本数15の棄却域を参考に、正規性の仮定をチェックする
順を追って解説していきます。
標本$r$次モーメントを計算する関数mrを定義する
def mr(arr, r, n):
mr = np.sum((arr - np.mean(arr))** r) / n
return mr$$m’_r = \sum(X_i – \bar{X})^r/ n$$
関数mrを利用し、標本歪度$b_1$と標本尖度$b_2$をデータA、データBについてそれぞれ計算する
for i, arr in enumerate(arrs):
m2 = mr(arr, 2, n)
m3 = mr(arr, 3, n)
m4 = mr(arr, 4, n)
b1 = m3 / (m2 ** (3/2))
b2 = m4 / (m2 ** 2) - 3
print(f'標本{i + 1}の標本歪度: {b1}')
print(f'標本{i + 1}の標本尖度: {b2}')
$$b_1 = \frac{m’_3}{(m’_2)^{3/2}}$$
$$b_2 = \frac{m’_4}{(m’_2)^2} – 3$$
標本数15の棄却域を参考に、正規性の仮定をチェックする
if b1 > 0.9 or b2 > 1.1:
print('有意水準5%で母分布が正規分布という仮定は棄却される')
else:
print('有意水準5%で母分布が正規分布という仮定は棄却されない')
本書より、標本数15の時の標本歪度$b_1$と標本尖度$b_2$の上側5%点はそれぞれ0.9/1.1であるので、本問題のデータA/Bの標本歪度$b_1$と標本尖度$b_2$と比較して、オーバーしている場合には正規性の仮定を棄却することができます。
今回のデータの場合は正規確率紙に描画したときに、裾の広さが可視化されていたデータBの標本について標本尖度の値が1.1より2倍ほど大きいことにより、正規性の仮定が棄却されました。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第7章-演習問題7「正規性の仮定のチェック」をPythonで解きました。
正規分布という分布が何かと便利であることを考えると、まず最初に正規性の仮定を検定してから、その他の定理等を当てはめて考えるのは、これまた頑健性の高い取り組みといえます。
皆さんも正規性の仮定できそうなデータが見つかった際には今回実施したような標本r次モーメントを活用した検定を行ってみてください!





コメント