
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題7「$\pi$の数字の一様性」にPythonを適用して問題を解いていきたいと思います。
一様分布を仮定した場合の$\chi^2$適合度検定のPython実装について学ぶことができるので、ぜひ参考にしていただけると幸いです!
問題文
<$\pi$の数字の一様性>
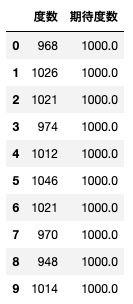
円周率$\pi$の小数点以下の数字の並びの内訳は下表の通りである。
小数点以下の数字が等確率で出現するという帰無仮説を各桁数ごとに検定せよ。
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 演習問題 P176
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
実装コード
本問題を解くためのコードは以下の通りです。
import numpy as np
import pandas as pd
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
import math
import warnings
warnings.simplefilter('ignore')
df = pd.read_csv('Uniformity_of_pi_numbers.csv', index_col = 0)
display(df)
# 全ての桁数を作成
Ns = [10 ** n for n in np.arange(4,10)]
# カイ二乗値を計算する関数
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
# 桁数ごとにカイ二乗値を計算し、検定を行う
for i, n in enumerate(Ns):
print(f'桁数が10^{i + 4}桁の時: ')
extract_df = pd.DataFrame(df.iloc[i,:])
extract_df.columns = ['度数']
# 一様分布を仮定
extract_df['期待度数'] = n / 10
chi_squ = calc_chi_square(extract_df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(extract_df) - 1
print(f'自由度: {v}')
alpha = 0.05
# 自由度と有意水準からカイ分布の値を計算
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('小数点以下の数字が等確率で出現するという仮定は有意水準5%で適合しない')
else:
print('小数点以下の数字が等確率で出現するという仮定は有意水準5%で適合する')
print()
print()実装コード解説
今回の問題は以下3ステップで解くことができます。
- それぞれの計算に使用する桁数を作成
- $\chi^2$値を計算する関数を定義
- 桁数ごとに$\chi^2$値を計算し、$\chi^2$適合度検定を行う
順を追って解説していきます。
それぞれの計算に使用する桁数を作成
今回の問題では小数点以下$10^4$〜$10^9$の桁数について考えていくので、まずは$10^4$〜$10^9$の数字を作っておきましょう。
この数字に基づいて、一様分布($=$全ての数字0〜9が等確率で出現することを仮定)を計算します。
# 全ての桁数を作成
Ns = [10 ** n for n in np.arange(4,10)]$\chi^2$値を計算する関数を定義
次に、観測度数(今回の場合はそれぞれの数字のカウント数)と期待度数(今回の場合は$10^k$を各数字$10$で割った数)を使用して、$\chi^2$値を計算していきます。
$\chi^2$値は以下の式で計算することができます。
$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$
# カイ二乗値を計算する関数
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi桁数ごとに$\chi^2$値を計算し、$\chi^2$適合度検定を行う
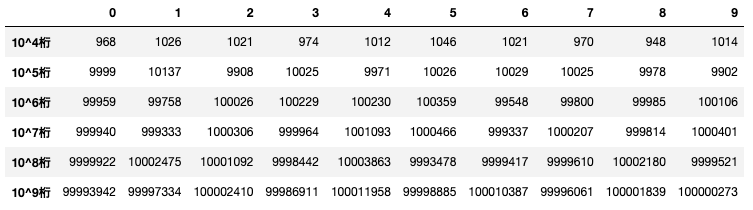
最後に$10^4,~\cdots,~10^9$桁ごとの度数と期待度数を利用して、$\chi^2$値を計算し、$\chi^2$分布の値と比較をしながら、一様分布の仮定が適合しているのかを検定していきます。
なお、先ほども述べたとおり、一様分布の仮定により、$10^k$桁の場合にはそれぞれの数字0〜9の期待度数は$\frac{10^k}{10}=10^{k-1}$であると仮定しています。
# 桁数ごとにカイ二乗値を計算し、検定を行う
for i, n in enumerate(Ns):
print(f'桁数が10^{i + 4}桁の時: ')
extract_df = pd.DataFrame(df.iloc[i,:])
extract_df.columns = ['度数']
# 一様分布を仮定
extract_df['期待度数'] = n / 10
chi_squ = calc_chi_square(extract_df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1)
v = len(extract_df) - 1
print(f'自由度: {v}')
alpha = 0.05
# 自由度と有意水準からカイ分布の値を計算
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('小数点以下の数字が等確率で出現するという仮定は有意水準5%で適合しない')
else:
print('小数点以下の数字が等確率で出現するという仮定は有意水準5%で適合する')
print()
print()上記コードを実行すると、以下のように各桁における$\chi^2$適合度検定の結果が出力されます。

まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題7「$\pi$の数字の一様性」をPythonで実装した場合のコードについて解説いたしました。
$\chi^2$適合度検定は特定の分布やモデルの仮定に対して、その当てはまりの良さを検定することができる便利な手段なので、皆さんもぜひ活用してみて下さい!




コメント