
こんにちは!データサイエンティストの青木和也(https://twitter.com/kaizen_oni)です!
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題5「適合度検定: 得点データへの分布の当てはめ」にPythonを適用して問題を解いていきたいと思います。
今回の問題ではポアソン分布や負の二項分布などのマーケティング領域でよく使われる分布が出てきますので、みなさんもぜひマーケティング分野において$\chi^2$検定を行いたい場合には、本記事の実装を調整して活用してみてください!
問題文
<適合度検定: 得点データへの分布の当てはめ>
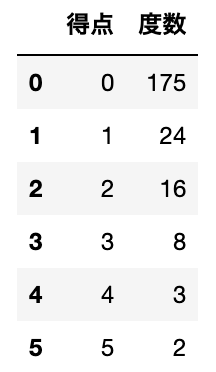
次表は1991年度プロ野球の西武対近鉄26試合での西武の1イニングごとの得点の分布である。
(i) 得点の平均$\bar{x}$と不偏分散$s^2$を求めよ
(ii) 得点に$\bar{x}$を平均とするポアソン分布を当てはめよ。その際、得点4と5は期待度数が少ないので、1つに併合せよ。さらに、この当てはめが良くないことを$\chi^2$適合度検定を用いて確認せよ。
(iii) ポアソン分布の当てはめがうまくいかないので、負の二項分布
$$ p(x) = \binom{a + x -1}{x}p^a(1-p)^x$$
の当てはめを試みる。ポアソン分布は平均と分散が等しいが、負の二項分布は平均よりも分散の方が大きいからである。負の二項分布の母数$p,a$の推定法の一つはモーメント法で、それは
$$ \hat{p} = \frac{\bar{x}}{s^2},~\hat{a} = \frac{\bar{x}^2}{(s^2-\bar{x})}$$
とするものである。これらの推定値を求め、負の二項分布を当てはめよ。当てはめの良さを$\chi^2$適合度検定を用いてチェックせよ。
(注)任意の実数$a$と非負整数$r$に対して
$$ \binom{a}{r} = \frac{a(a-1)\cdots(a-r+1)}{r!}$$
と定義する。ただし、$\binom{a}0 = 1$とする
東京大学教養学部統計学教室『自然科学の統計学』(東京大学出版社/2001) 第5章 演習問題 P175
今回の演習で使用するCSVデータは以下記事からダウンロードすることが可能です。
実装コード(i)(ii)
問題(i)(ii)の実装コードは以下のとおりです。
import numpy as np
import pandas as pd
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
import math
df = pd.read_csv('Fitting_Distributions_to_Scoring_Data.csv')
display(df)
# (1)
n = df['度数'].sum()
x_mean = (df['得点'] * df['度数']).sum() /n
u_var = (df['度数'] * (df['得点'] - x_mean) ** 2).sum() / (n - 1)
print(f'平均得点: {x_mean}')
print(f'不偏分散: {u_var}')
# (2)
def poisson(x):
prob = np.exp(-x_mean)* x_mean ** x / math.factorial(x)
return prob
df['確率(ポアソン)'] = df['得点'].map(poisson)
df['期待度数(ポアソン)'] = df['確率(ポアソン)'] * n
# 得点4と5をまとめる
df.loc[6] = ["4,5", df.loc[4:, '度数'].sum(), df.loc[4: , '確率(ポアソン)'].sum(), df.loc[4:, '期待度数(ポアソン)'].sum()]
df = df.drop([4,5], axis = 0)
display(df)
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数(ポアソン)']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1 - ポアソン分布の母数の数)
v = len(df) - 1 - 1
print(f'自由度: {v}')
alpha = 0.05
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('ポアソン分布は有意水準5%で適合しない')
else:
print('ポアソン分布は有意水準5%で適合する')そして、(iii)の実装コードは以下のとおりです。
何度も計算を見直したのですが、(iii)において導出した$\chi^2$値が書籍の模範解答$\chi^2=5.94$とは異なり、$\chi^2=6.454$となっております。
もし、本実装コードについて誤りを見つけた方はコメント等にてご一報いただけると幸いです。
import numpy as np
import pandas as pd
# カイ二乗値をLaTeX形式で表示するためにmatplotlibを使用
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
from scipy.stats import chi2
import math
df = pd.read_csv('Fitting_Distributions_to_Scoring_Data.csv')
display(df)
n = df['度数'].sum()
x_mean = (df['得点'] * df['度数']).sum() /n
u_var = (df['度数'] * (df['得点'] - x_mean) ** 2).sum() / (n - 1)
print(f'平均得点: {x_mean}')
print(f'不偏分散: {u_var}')
# pとaを算出
p = x_mean / u_var
print(f'p = {p}')
a = x_mean ** 2/ (u_var - x_mean)
print(f'a = {a}')
def negative_binomial(x):
prob = p ** a * (1-p) ** x * math.gamma(a + x) / (math.gamma(x + 1) * math.gamma(a))
return prob
df['確率(負の二項分布)'] = df['得点'].map(negative_binomial)
df['期待度数(負の二項分布)'] = df['確率(負の二項分布)'] * n
# 得点4と5をまとめる
df.loc[6] = ["4,5", df.loc[4:, '度数'].sum(), df.loc[4: , '確率(負の二項分布)'].sum(), df.loc[4:, '期待度数(負の二項分布)'].sum()]
df = df.drop([4,5], axis = 0)
display(df)
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数(負の二項分布)']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
# 自由度 (度数の数 - 1 - ポアソン分布の母数の数)
v = len(df) - 1 - 2 # 母数はp,aの2つ
print(f'自由度: {v}')
alpha = 0.05
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('負の二項分布は有意水準5%で適合しない')
else:
print('負の二項分布は有意水準5%で適合する')実装コード解説
(i)平均と不偏分散の導出
まずは平均の導出と不偏分散の導出について、それぞれ見ていきましょう
平均の導出
本問題における平均は、得点ごとの度数がまとまっているため、期待値のように得点と度数をかけ算して、最後に全体の数$n$で割り算をすることによって求めることができます。
n = df['度数'].sum()
x_mean = (df['得点'] * df['度数']).sum() /n不偏分散の導出
不偏分散とは以下のように定義されています。
標本分散とは、母分散を過大にあるいは過小にではなく不偏(=偏りなく)に推定する分散であり、標本$X_1, X_2, \cdots, X_n$の標本平均を$\bar{X}$とすると、以下のように定義される。
$$ s^2 = \frac{1}{n-1}\{(X_1 – \bar{X})^2 + (X_2 – \bar{X})^2+\cdots +(X_n – \bar{X})\}=\frac1{n-1}\sum_{i=1}^n \{(X_i – \bar{X})^2\}$$
また、$s^2$の期待値は以下のようになり、不変性を示している.
$$ E(s^2) = \sigma^2$$
東京大学教養学部統計学教室『統計学入門』(東京大学出版社/2001) 第9章 標本分布 P184を参考に、ブログ主が文章を再構成
ここで、今回の問題では、標本$X_1, \cdots, X_n$のパターンは0,1,2,3,4,5の6パターンしかないため、度数を使用して以下のようにまとめることができます。
$$ s^2 =\frac{1}{n-1}\sum_{i=1}^n \{(X_i – \bar{X})^2\}=\frac1{n-1}\{ 175\times( 0 – \bar{X})^2 + \cdots + 2 * (5 – \bar{X})^2\}$$
よって、不偏分散を求めるコードは以下のようになります。
u_var = (df['度数'] * (df['得点'] - x_mean) ** 2).sum() / (n - 1)
print(f'平均得点: {x_mean}')
print(f'不偏分散: {u_var}')
(ii)ポアソン分布当てはめに対する$\chi^2$適合度検定の実施
続いて、ポアソン分布をもとに期待度数を求め、その当てはまり具合を$\chi^2$適合度検定を用いてチェックする段階ですが、以下のような手順で実行していきます。
- ポアソン分布を求める関数を定義する
- ポアソン分布に基づいて確率と期待度数を求める
- 度数と期待度数(ポアソン分布)に基づいて$\chi^2$値を求める
- 自由度を求め、求めた$\chi^2$値と$\chi^2$分布の値を比較する
順を追って説明していきましょう。
ポアソン分布を求める関数を定義する
まずは、ポアソン分布を求める関数を定義します。
ポアソン分布は平均$\lambda$に対して以下のように定義されます。
$$ f(x) = \frac{e^{-\lambda}\lambda^x}{x!}$$
def poisson(x):
prob = np.exp(-x_mean)* x_mean ** x / math.factorial(x)
return probポアソン分布に基づいて確率と期待度数を求める
先ほど定義したポアソン分布を使用して、得点に対応する確率と期待度数を求めます。
df['確率(ポアソン)'] = df['得点'].map(poisson)
df['期待度数(ポアソン)'] = df['確率(ポアソン)'] * nこの時、問題文中で「得点4と5は期待度数が少ないので、1つに併合せよ。」と指示されているので、得点4と5の期待度数を足し算して、新たな行を追加し、元の得点4,5の行を削除しましょう。
# 得点4と5をまとめる
df.loc[6] = ["4,5", df.loc[4:, '度数'].sum(), df.loc[4: , '確率(ポアソン)'].sum(), df.loc[4:, '期待度数(ポアソン)'].sum()]
df = df.drop([4,5], axis = 0)
display(df)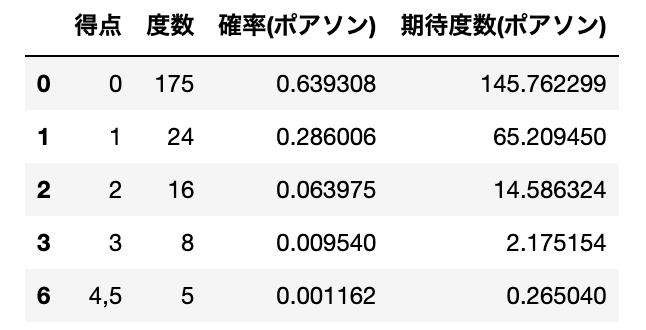
度数と期待度数(ポアソン分布)に基づいて$\chi^2$値を求める
先ほど求めた期待度数(ポアソン)と度数を使用して、$\chi^2$値を算出します。
なお、$\chi^2$値は以下の式で計算することができます。
$$ \chi^2 = \sum_i^{n} \frac{(度数_i – 期待度数_i)^2}{期待度数_i}$$
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数(負の二項分布)']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()
自由度を求め、求めた$\chi^2$値と$\chi^2$分布の値を比較する
最後に今回の期待度数における自由度を求め、自由度と有意水準を使って$\chi^2$分布の値を求めて、適合度検定を完了させましょう。
ここで、自由度は以下のように計算されることに注意をしましょう。
$$ 自由度\nu = (度数の数-1) – (あてはめたモデルの母数の個数)$$
今回の問題においては、ポアソン分布を算出する際に「平均$\bar{x}$」という母数を使用しているので、自由度は以下のコードのようにして求められます。
# 自由度 (度数の数 - 1 - ポアソン分布の母数の数)
v = len(df) - 1 - 1
print(f'自由度: {v}')
自由度と有意水準を使用して、$\chi^2$適合度検定を行うと、以下のように「ポアソン分布は適合しない」という結論が得られます。
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('ポアソン分布は有意水準5%で適合しない')
else:
print('ポアソン分布は有意水準5%で適合する')
このようにして、得点分布にポアソン分布を適合するのは有意水準5%で適していないことがわかりました。
(iii)負の二項分布当てはめに対する$\chi^2$適合度検定の実施
次に、負の二項分布を元データに当てはめて、$\chi^2$適合度検定を実施していきたいと思います。
ポアソン分布と同様に以下の4ステップで解き進めていきます。
- 負の二項分布を求める関数を定義する
- 負の二項分布に基づいて確率と期待度数を求める
- 度数と期待度数(負の二項分布)に基づいて$\chi^2$値を求める
- 自由度を求め、求めた$\chi^2$値と$\chi^2$分布の値を比較する
順を追って説明していきましょう。
負の二項分布とは?
負の二項分布とは、以下のように定義されています。
$k$回目の成功を得るまでの失敗回数を$x$とすれば、$x=0,1,2,\cdots$で、その確率は
$$ f(x) = {}_{k+x-1}\mathrm{C}_x p^k (1-p)^x$$
として定義される。これを負の二項分布という。
東京大学教養学部統計学教室『統計学入門』(東京大学出版社/2001) 第6章 確率分布 P118を参考に、ブログ主が文章を再構成
負の二項分布を求める関数を定義する
まずは、負の二項分布を求める関数を定義します。
負の二項分布は母数$p,a$に対して以下のように定義されます。
$$ p(x) = \binom{a + x -1}{x}p^a(1-p)^x$$
なお、ここで登場する$p$は成功確率、$a$は考慮すべき成功回数(=今回の場合であれば得点)を表す負の二項分布の母数であり、問題文にあるとおり、以下のような式によって推定されます。
$$ \hat{p} = \frac{\bar{x}}{s^2}$$
$$ \hat{a} = \frac{\bar{x}^2}{(s^2-\bar{x})}$$
上記母数を推定するコードを実装すると以下のようになります。
# pとaを算出
p = x_mean / u_var
print(f'p = {p}')
a = x_mean ** 2/ (u_var - x_mean)
print(f'a = {a}')上記コードで求めた母数$p,a$を使用すると、負の二項分布は以下のコードで求めることができます。
def negative_binomial(x):
prob = p ** a * (1-p) ** x * math.gamma(a + x) / (math.gamma(x + 1) * math.gamma(a))
return probmath.gammaってなに?
通常、Pythonで階乗を実装するときはmath.factorial()というメソッドを使用します。
math.factorial(4)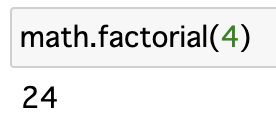
そして、今回の問題でも$\binom{a + x-1}{x}$の計算のところで階乗を使用するように指示されています。
$$ \binom{a}{r} = \frac{a(a-1)\cdots(a-r+1)}{r!}$$
一方で、今回の問題では、$a$が浮動小数点を持つような実数であることが計算結果からわかっています。
実は、math.factorial()メソッドは正の整数以外の値に対して適用することができないのです。
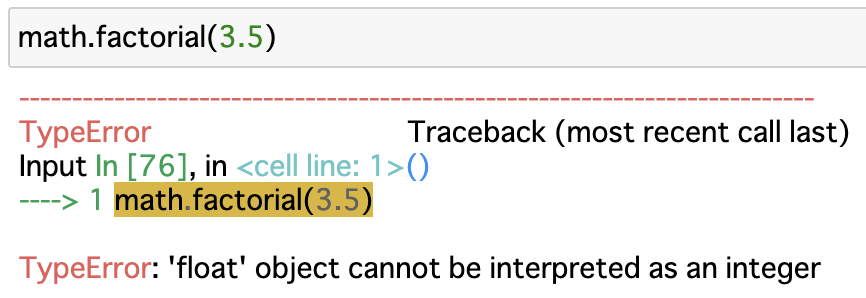
そのため、今回の実装では、階乗という概念を実数まで拡張したガンマ関数を使用しています。
なお、$a$が実数のとき、階乗とガンマ関数$\Gamma$の間には以下のような関係が成り立っています。
$$ a! = \Gamma(a+1)$$
なぜ$\binom{a+x-1}{x}$がmath.gamma(a + x) / (math.gamma(x + 1) * math.gamma(a))になるの?
上記については、$a$が正の整数と仮定すると以下のように式変形ができます。
$$ \binom{a+x-1}{x} = \frac{(a+x-1)(a+x-2)\cdots(a+1)}{x!}$$
$$ = \frac{(a+x-1)(a+x-2)\cdots(a+1)a(a-1)\cdots 1}{x!a!}$$
さらに式変形すると以下のようになります。
$$ \frac{(a+x-1)(a+x-2)\cdots(a+1)a(a-1)\cdots 1}{x!a!} = \frac{(a+x-1)!}{x!a!}$$
ここで、$a$が正の整数の時は、以下のようにガンマ関数に置き換えることが可能です。
$$\frac{(a+x-1)!}{x!a!} = \frac{\Gamma(a+x)}{\Gamma(x+1)\Gamma(a+1)}$$
上式の右辺がそのまま以下のようにコードとして実装されているのです。
math.gamma(a + x) / (math.gamma(x + 1) * math.gamma(a))負の二項分布に基づいて確率と期待度数を求める
先ほど定義した負の二項分布を使用して、得点に対応する確率と期待度数を求めます。
df['確率(負の二項分布)'] = df['得点'].map(poisson)
df['期待度数(負の二項分布)'] = df['確率(負の二項分布)'] * nこの時、問題文中で「得点4と5は期待度数が少ないので、1つに併合せよ。」と指示されているので、得点4と5の期待度数を足し算して、新たな行を追加し、元の得点4,5の行を削除しましょう。
# 得点4と5をまとめる
df.loc[6] = ["4,5", df.loc[4:, '度数'].sum(), df.loc[4: , '確率(負の二項分布)'].sum(), df.loc[4:, '期待度数(ポアソン)'].sum()]
df = df.drop([4,5], axis = 0)
display(df)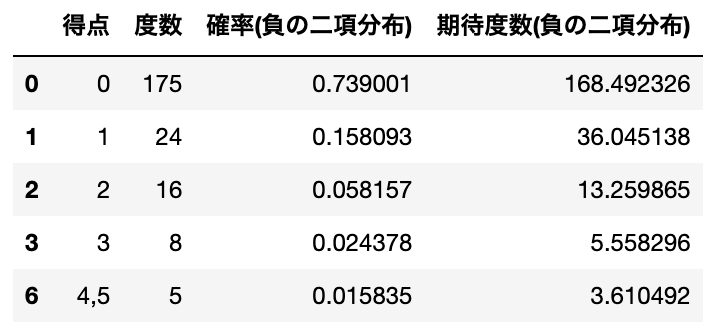
度数と期待度数(負の二項分布)に基づいて$\chi^2$値を求める
先ほど求めた期待度数(負の二項分布)と度数を使用して、$\chi^2$値を算出します。
ここの$\chi^2$値の計算結果が書籍の解答例と一致しません。
実装で誤りがあった場合には、コメント等でご指摘いただけると幸いです。
def calc_chi_square(df):
sum_chi = 0
for index, row in df.iterrows():
obj = df.at[index, '度数']
exp = df.at[index, '期待度数(負の二項分布)']
# カイ二乗値を計算
sum_chi += (obj - exp) ** 2/exp
return sum_chi
chi_squ = calc_chi_square(df)
txt = r"$\chi^2 = $" + str(chi_squ)
# matplotlibのLaTeXを利用して出力
fig, ax = plt.subplots(figsize = (0,0))
plt.text(0,0,txt, fontsize = 14)
ax = plt.gca()
ax.axis('off')
plt.show()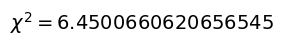
自由度を求め、求めた$\chi^2$値と$\chi^2$分布の値を比較する
最後に今回の期待度数における自由度を求め、自由度と有意水準を使って$\chi^2$分布の値を求めて、適合度検定を完了させましょう。
ここで、自由度は以下のように計算されることに注意をしましょう。
$$ 自由度\nu = (度数の数-1) – (あてはめたモデルの母数の個数)$$
今回の問題においては、負の二項分布を算出する際に$p,a$という2つの母数を使用しているので、自由度は以下のコードのようにして求められます。
# 自由度 (度数の数 - 1 - 負の二項分布の母数の数)
v = len(df) - 1 - 2
print(f'自由度: {v}')
自由度と有意水準を使用して、$\chi^2$適合度検定を行うと、以下のように「負の二項分布は適合しない」という結論が得られます。
print(f'自由度: {v}')
alpha = 0.05
chi2_pdf = chi2.ppf(1 - alpha , v)
print(f"自由度{v}の有意水準5%におけるカイ二乗値: {chi2_pdf}")
if chi_squ > chi2_pdf:
print('負の二項分布は有意水準5%で適合しない')
else:
print('負の二項分布は有意水準5%で適合する')
このようにして、得点分布に負の二項分布を適合するのは有意水準5%で適していないことがわかりました。
教科書では負の二項分布を適合した時の$\chi^2=5.94$となっているため、有意水準5%で負の二項分布は適合する、という結論になっています。
まとめ
今回の記事では、統計学の青本「自然科学の統計学」の第5章-演習問題5「適合度検定: 得点データへの分布の当てはめ」にPythonを適用して問題を解いていきました。
今回の実装では、データから平均値や不偏分散、仮定する分布の母数などを求めながら、分布との適合について$\chi^2$値を使用して検定を行いました。
なお、本文でも指摘しているように、負の二項分布に対する$\chi^2$値が教科書と乖離してしまっているため、教科書の結論と少し異なって結論になっています。
もし、実装コードやロジックに不備を見つけた場合はコメント等でご指摘いただけると幸いです。




コメント